Simultaneous Equations
Simultaneous Equations Revision
Simultaneous Equations
Simultaneous equations are equations that share the same variables. There will be a solution, or solutions, that work for all equations. In A level maths, you will only see simultaneous equations in two variables, e.g. x and y.
There are 2 main methods used to solve simultaneous equations.
Method 1: Elimination
The method of elimination is used when there are two linear simultaneous equations. We eliminate one variable by subtracting one equation from the other.
Example: Solve the following equations:
\begin{aligned} 3x + 7y -44 &= 0 \\ 2x + 3y &= 21 \end{aligned}
Step 1: Write both equations in the form ax+by=c, if necessary:
\begin{aligned} 3x + 7y &= 44 \\ 2x + 3y &= 21 \end{aligned}
Step 2: Manipulate the equations so that the coefficients match – multiply the equations to make either the x‘s or y‘s equal in size (ignoring the signs). Always multiply to get the LCM of the coefficients.
\,(\times2) \,\,\,\,\,\,\,\,\,3x + 7y = 44\,\,\, \Rightarrow \,\,\, 6x + 14y = 88
(\times3)\,\,\,\,\,\,\,\,\, 2x+3y = 21 \,\,\, \Rightarrow \,\,\, 6x+9y=63
Step 3: Add or subtract the equations to eliminate variable that has terms with equal coefficients, so that you can find the other variable.
In this case, both equations have +6x, so we need to subtract:
\begin{aligned}6x + 14y &= 88 \\ (-)\,\,\,\,\,\,\,\,\, 6x+9y&=63 \\ \hline 5y&=25\end{aligned}
Step 4: Solve the resulting equation.
In this case, we need to solve the equation to find y
\begin{aligned}(\div 5)\,\,\,\,\,\,\,\,\,5y&=25 \\ \textcolor{red}{y} &\textcolor{red}{= 5} \end{aligned}
Step 5: Find the variable that you eliminated.
In this case, replace (substitute) y = 5 into one of the equations and solve to find x:
\begin{aligned} 2x + 3y &= 21 \\ 2x + 3(5) &= 21 \\ 2x + 15 &= 21 \\ 2x &= 6 \\ \textcolor{blue}{x} &\textcolor{blue}{= 3} \end{aligned}
Hence,
\textcolor{blue}{x = 3} and \textcolor{red}{y = 5}
Method 2: Substitution
We use the method of substitution when one of the simultaneous equations is quadratic (non-linear), since we can’t use the method of elimination.
Example: Solve
\begin{aligned} x^2 + 2y &= 31 \\ x+y &= 14 \end{aligned}
Step 1: Rearrange the linear equation so that one of the variables is on its own (in this case it will be easier to get y on its own so that we don’t have to do any squaring of brackets)
\begin{aligned} (-x) \,\,\,\,\,\, x+y &= 14 \\ y &= -x + 14 \end{aligned}
Step 2: Substitute this variable into the quadratic equation, so that there is an equation in only one variable.
y = -x + 14 so replace y with -x + 14:
x^2 + 2(-x+14) = 31
Step 3: Expand and solve to find the values for one variable.
\begin{aligned} x^2 + 2(-x+14) &= 31 \\ x^2 - 2x + 28 &= 31 \\ x^2 - 2x - 3 &= 0 \\ (x-3)(x+1) &= 0 \end{aligned}
Hence,
\textcolor{red}{x = 3} and \textcolor{red}{x = -1}
Step 4: Substitute these values into the linear equation (since this will be easier) and solve to find the corresponding values of the other variable.
When \textcolor{red}{x = 3}, \textcolor{blue}{y} = -3+14 = \textcolor{blue}{11}
When \textcolor{red}{x = -1}, \textcolor{blue}{y} = -(-1) + 14 = \textcolor{blue}{15}
So, there are two pairs of solutions
\textcolor{red}{x=3}, \textcolor{blue}{y = 11} and \textcolor{red}{x = -1}, \textcolor{blue}{y = 15}
Note: You may need to use the quadratic formula if you get a quadratic equation that is too difficult to solve by factorising.
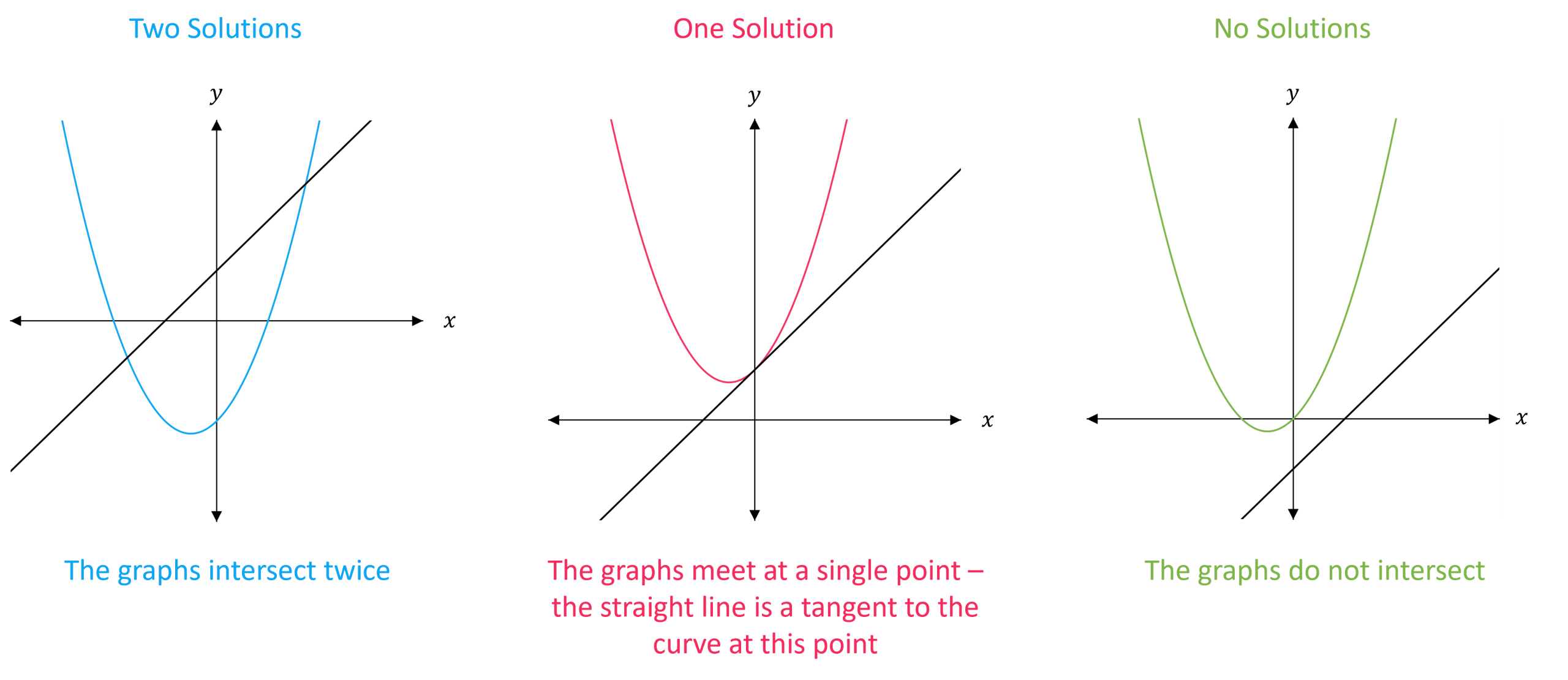
Interpreting Simultaneous Equations Geometrically
To interpret simultaneous equations geometrically, we need to draw a sketch of the two functions and describe what we see.
The number of solutions is equal to the number of intersections between the graphs:
Two solutions – the graphs intersect twice
One solution – the graphs meet at a single point – the graph is a tangent to the curve at this point
No solutions – the graphs do not intersect
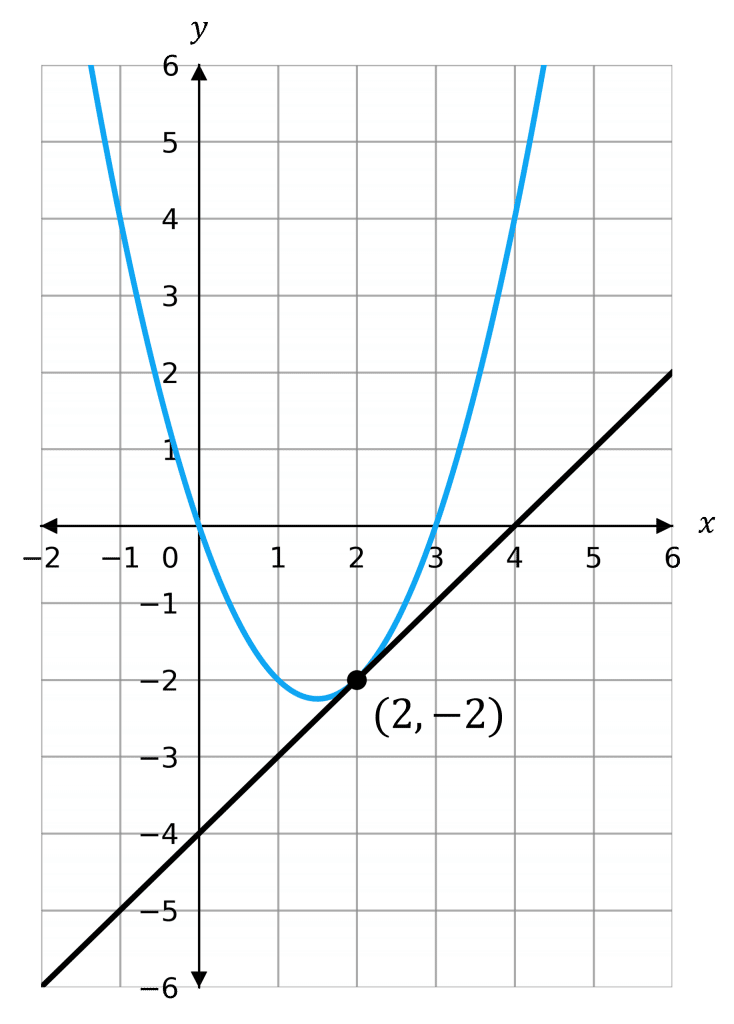
Example: Interpreting Simultaneous Equations Geometrically
Interpret the following geometrically:
y = x^2 - 3x and y = x - 4
[4 marks]

Substitute y=x-4 into y = x^2 - 3x, and then solve for x:
\begin{aligned} x - 4 &= x^2 - 3x \\ x^2 - 4x + 4 &= 0 \\ (x-2)^2 &= 0 \\ \textcolor{red}{x} &\textcolor{red}{= 2} \end{aligned}
Then, substitute \textcolor{red}{x = 2} into y = x - 4 and solve for y:
\begin{aligned} y &= x - 4 \\ y &= 2 - 4 \\ \textcolor{blue}{y} &\textcolor{blue}{= -2} \end{aligned}
Hence, there is only one solution \textcolor{red}{x = 2}, \textcolor{blue}{y = -2}
Therefore, the graphs will meet at a single point: (\textcolor{red}{2}, \textcolor{blue}{-2})
So, the straight line is a tangent to the curve at the point (\textcolor{red}{2},\textcolor{blue}{-2})
Simultaneous Equations Example Questions
Question 1: Solve 4x + y = 18 and 3x + 2y = 21
[4 marks]
Multiply the first equation by 2 so that they coefficients of y match:
\begin{aligned} 8x + 2y &= 36 \\ 3x + 2y &= 21 \end{aligned}
Subtract the second equation from the first, to eliminate the y variable:
5x = 15
And then solve:
x = 3
Then, substitute x =3 into either equation and solve:
\begin{aligned} 4(3) + y &= 18 \\ 12 + y &= 18 \\ y &= 6 \end{aligned}
Hence,
x = 3 and y = 6
Question 2: Find the coordinates of the point of intersection of x^2 + y^2 = 100 and x-y=2.
[6 marks]
Rearrange x-y=2 so that x is on its own:
x = y+2
Then, substitute this into x^2 + y^2 = 100 and expand and solve for y:
\begin{aligned} (y+2)^2 + y^2 &= 100 \\ y^2 + 4y + 4 + y^2 &= 100 \\ 2y^2 + 4y - 96 &= 0 \\ (2y-12)(y+8) &= 0 \end{aligned}
Hence, 2y - 12 = 0 and y + 8 = 0 \Rightarrow y = 6 and y = -8
Substitute these values into the non-linear equation, to find the values of x:
y = 6 \Rightarrow x = 6+2 = 8
y = -8 \Rightarrow x = -8 + 2 = -6
Hence, the points of intersection are (8, 6) and (-6, -8)
Question 3: Show that the pair of equations y = x and y = x^2 + 5x + 5 have no real solutions.
[3 marks]
Substitute y = x into y = x^2 + 5x + 5, and solve:
\begin{aligned} x^2 + 5x + 5 &= x \\ x^2 + 4x + 5 &= 0 \\ (x+2)^2 - 4 + 5 &= 0 \\ (x+2)^2 + 1 &= 0 \\ (x+2)^2 &= -1 \end{aligned}
You cannot get a real number from square rooting a negative number. Therefore there are no real solutions.
You could have found the discriminant of x^2 +4x + 5:
b^2 - 4ac = 4^2 - 4 \times 1 \times 5 = 16 - 20 = -4
The discriminant is <0, so there are no real roots, and therefore no real solutions.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






