Connected Particles
Connected Particles Revision
Connected Particles
By a connection, we mean a system where multiple particles are linked by another force. For example, a car pulling a caravan is connected by the coupling, which provides tension on both objects.
Make sure you are happy with the following topics before continuing.
Assumptions
First off, we have to assume that pulleys, pegs and other potential external factors are smooth, unless explicitly told otherwise.
We’ll also treat multiple connected particles as one mass, with the same velocity and acceleration. Without this, we could assume the connection has failed between the two particles, i.e. a linked piece of string has snapped, or slackened.
We’re also going to assume that Newton’s Laws hold, especially the Second Law, F = ma. In fact, we’re going to use F = ma in the direction that each particle moves individually.
Otherwise, we resolve forces exactly how we would anyway, taking each particle separately.
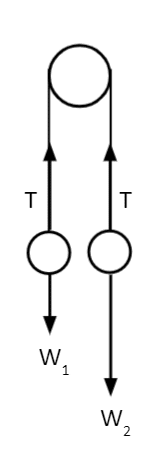

Example 1: Yo-yo System
Back in Question 1 in the Forces section, we had two balls attached by taut string, suspended by a smooth peg.
We said that Ball 2 has twice the mass of Ball 1. Given that Ball 1 has a mass of 60\text{ g} and starts 30\text{ cm} below the peg, calculate the tension in the string and the time taken for Ball 1 to reach the peg.
[4 marks]
Resolving for Ball 1:
T - (0.06 \times 9.8) = T - 0.588 = 0.06a
Resolving for Ball 2:
(0.12 \times 9.8) - T = 1.176 - T = 0.12a
From here, we have
0.12a = 2T - 1.176 = 1.176 - T
which can be rearranged to
3T = 2.352, or T = 0.784\text{ N}
Substituting this back into one of our equations, we have 1.176 - 0.784 = 0.12a, meaning that Ball 2 has a downward acceleration of a = 3.27\text{ ms}^{-2}. This means that Ball 1 accelerates towards the peg at 3.27\text{ ms}^{-2} \text{ (to }2\text{ dp)}.
Using SUVAT, s = ut + \dfrac{1}{2}at^2 gives
0.3 = \dfrac{1}{2} \times 3.27 \times t^2, so t = 0.43\text{ seconds}
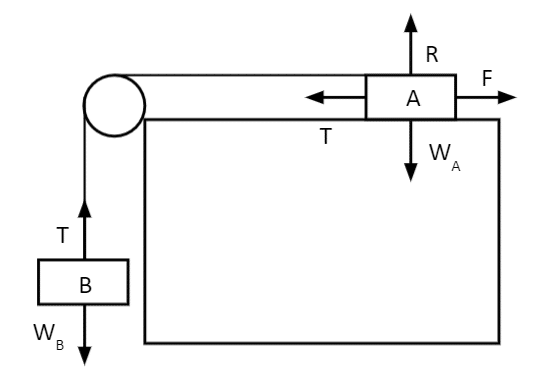

Example 2: Rough Planes
Now, imagine a system of two weights attached by a thin piece of taut rope, both of mass 4\text{ kg}. Weight \text{A} is rested on a rough table with a coefficient of 0.2, and weight \text{B} is suspended below a smooth pulley. What is the acceleration of both weights? What is the tension in the rope?
[5 marks]
Weight \text{A} (vertical):
R = mg = 4 \times 9.8 = 39.2\text{ N}
Weight \text{A} (horizontal):
T - \mu R = ma, giving T - (0.2 \times 39.2) = T - 7.84 = 4a
Weight \text{B} (vertical):
mg - T = ma, giving 39.2 - T = 4a
Therefore,
4a = 39.2 - T = T - 7.84
which can be rearranged to
2T = 47.04, or T = 23.52\text{ N}
Substituting back into one of our equations, we have 23.52 - 7.84 = 4a
giving
a = \dfrac{23.52 - 7.84}{4} = 3.92\text{ ms}^{-2}
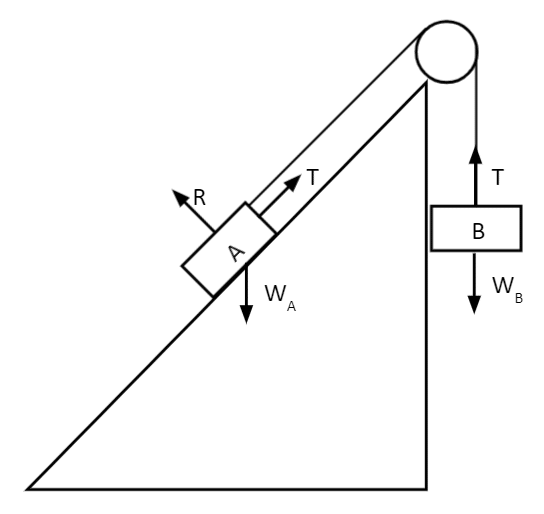

Example 3: Rough Inclined Planes
Here’s another system of two weights attached by a thin piece of taut rope. Weight \text{A}, of mass 9\text{ kg}, is now on an inclined plane at an angle of 45° with a coefficient of 0.1, and weight \text{B}, of mass 3\text{ kg} is suspended below a smooth pulley. Does weight \text{B} rise or fall? What is the rate of acceleration of both weights? What is the tension in the rope?
[7 marks]
Weight \text{A} (perpendicular to motion):
R = mg\cos 45° = (9 \times 9.8)\cos 45° = \dfrac{88.2}{\sqrt{2}}
Weight \text{A} (parallel to motion, down slope):
mg\sin 45° - T - F = mg\sin 45° - T - \mu R = ma
giving
(9 \times 9.8)\sin 45° - T - \left( 0.1 \times \dfrac{88.2}{\sqrt{2}}\right)
= \dfrac{88.2}{\sqrt{2}} - T - \dfrac{8.82}{\sqrt{2}} = 9a.
Weight \text{B} (upwards):
T - mg = ma, giving T - (3 \times 9.8) = 3a
or
T - 29.4 = 3a
Equating the two equations:
9a = 3T - 88.2 = \dfrac{79.38}{\sqrt{2}} - T
So
4T = \dfrac{79.38}{\sqrt{2}} + 88.2 = 144.33
giving
T = 36.08\text{ N(to }2\text{ dp)}
Therefore, we have
9a = (3 \times 36.08) - 88.2
so
a = 2.23\text{ ms}^{-2}
Connected Particles Example Questions
Question 1: We have two balls attached by taut string, suspended by a smooth peg.
If Ball \text{A} has mass 100\text{ g} and Ball \text{B} has mass 80\text{ g}, calculate the tension in the string and the acceleration of Ball \text{A}.
[4 marks]
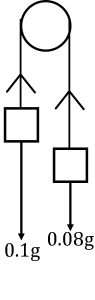
Note: Here, “0.1g” is not the same as 0.1\text{ grams}, it is 0.1\text{ kg} by the acceleration due to gravity, g. The same rule applies for 0.08g.
Resolving Ball \text{A}:
(0.1 \times 9.8) - T = 0.1a
Resolving Ball \text{B}:
T - (0.08 \times 9.8) = 0.08a
Therefore, we have
a = 9.8 - 10T = 12.5T - 9.8
So
22.5T = 19.6
giving
T = 0.871\text{ N (to }3\text{ dp)}
By extension, a = 1.088\text{ ms}^{-2}\text{ (to } 3\text{ dp)}
Question 2: For two bricks of mass 4\text{ kg} linked by a rope on a smooth pulley, find the tension in the rope. Assume that the surface that brick \text{A} has a coefficient of friction of 0.7.
[3 marks]
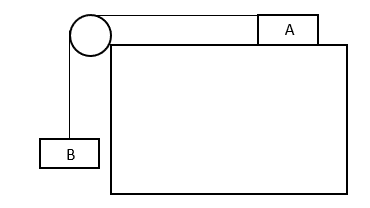
Brick \text{A} (vertical):
R = 4 \times 9.8 = 39.2\text{ N}
Brick \text{A} (horizontal):
T - \mu R = ma
gives
T - (0.7 \times 39.2) = 4a
Brick \text{B} (vertical):
(4 \times 9.8) - T = 4a
So
T - 27.44 = 39.2 - T
meaning
T = 33.32\text{ N}
Question 3: A truck on a flat surface is towing a car up a hill with an incline of 30°. Given that the truck weighs 2000\text{ kg}, and the car weighs 1000\text{ kg} and is exerting a thrust of 2500 \text{ N}, what thrust is required by the truck to pull the car up the hill with an acceleration of 1\text{ ms}^{-2}?
Assume the coefficient of friction of both the hill and the flat surface are 0.25.
[7 marks]
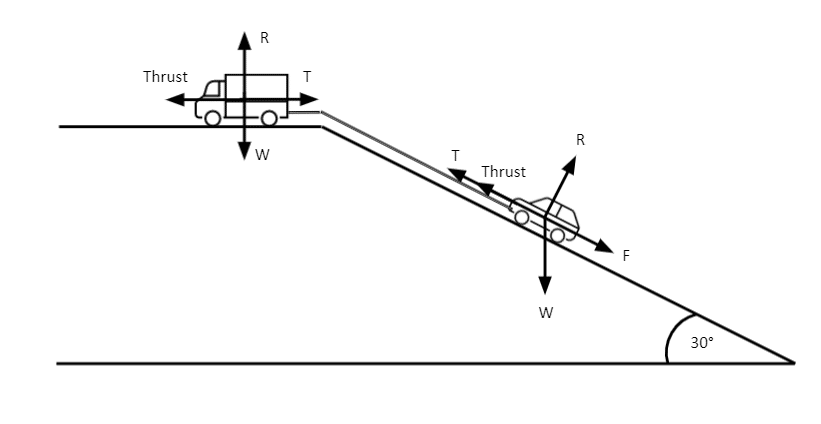
Resolving truck (vertically):
R = 2000 \times 9.8 = 19600\text{ N}
Resolving truck (horizontally):
\text{Thrust} - T - (0.25 \times 19600) = 2000
Resolving car (perpendicular to F):
(1000 \times 9.8)\cos 30° = 8487 = R
Resolving car (parallel to F):
2500 + T - (0.25 \times 8487) - (1000 \times 9.8)\sin 30° = 1000
From the last equation, we have
T = 1000 + 4900 + 2122 - 2500 = 5522\text{ N}
Back to the truck:
\text{ Thrust} - 5522 - 4900 = 2000
which gives
\text{Thrust} = 12422\text{ N}






