Friction

In the Forces section, we mentioned that friction was calculated by the equation $F \leq \textcolor{red}{\mu} R$ , where $\textcolor{red}{\mu}$ is known as the coefficient of friction, which has no units. As a general rule of thumb, the rougher a surface is, the higher its coefficient of friction.

We also have the term limiting friction, when friction is at its maximum. This is shown when $F = \textcolor{red}{\mu} R$ .

Make sure you are happy with the following topics before continuing.

Fundamentals

Example: Here’s a box on a flat surface with two people pushing and pulling in the same direction.

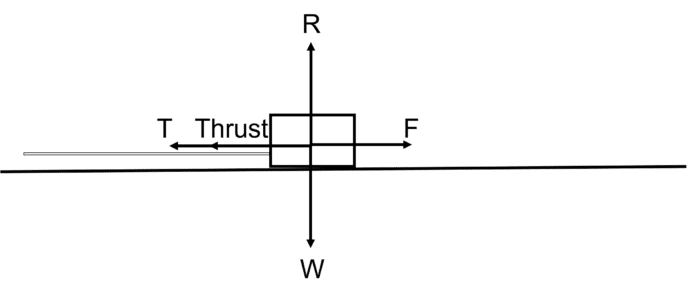
Let’s now say that the weight of the box, $W$ , is $100\text{ N}$ , and that the friction is limiting (i.e. applying any more force in $T$ or Thrust will cause the box to accelerate). Say, also, that the friction $F$ is $50\text{ N}$ .

Then we have the normal reaction force $R = 100\text{ N}$ .

Since $F = \textcolor{red}{\mu} R$ , the coefficient of friction, $\textcolor{red}{\mu} = \dfrac{50}{100} = 0.5$ .

Note:

By definition, the coefficient of friction $\mu$ is such that $\textcolor{red}{\mu} \geq 0$ . It is usually, but not always, less than $1$ .

Friction on a Tilted Plane

Example: Here’s a $1500 \text{ kg}$ car being towed up an incline at an angle of $30\degree$ . Say the slope has a coefficient of friction $\textcolor{red}{\mu} = 0.4$ . What would be the required combined force of the tension in the rope, $T$ , and the thrust from the car? Assume the car is travelling at constant velocity up the hill.

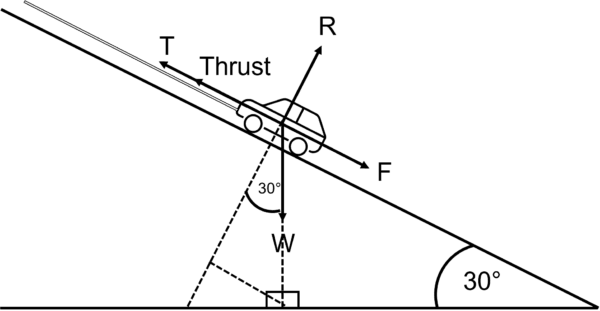
First, adapt this system by rotating it, to visualise the perpendicular forces a little more easily.

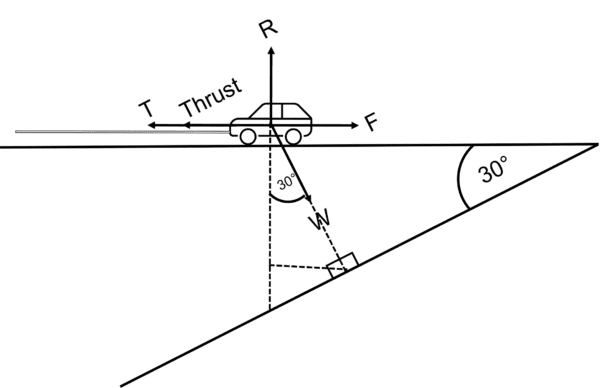
Perpendicular to $F$ , we have $R = W\cos 30°$ .

$W = 1500 \times 9.8 = 14700\text{ N}$ , so $R = 12730.57\text{ N}$

So, parallel to $F$ , we have $T + \text{Thrust} = F + W\sin 30°$ .

By $F_{max} = \textcolor{red}{\mu} R$ , the limit of friction is $F_{max} = 5092.23\text{ N}$

Since we have $W$ and $F_{max}$ , we can see that the minimum thrust and tension required to move the car up the slope is $5092.23 + W\sin 30° = 12442.23\text{ N}$ .

Friction Example Questions

Question 1: A box of mass $m\text{ kg}$ lays on a flat surface, with no vertical force applied. Find an expression for the potential friction force, $F$ , in terms of $\mu$ , $m$ and $g$ .

[2 marks]

We have $F \leq \mu R$ .

Since no other vertical forces are applied, we have $W = R$ .

We also have $W = mg$ .

Therefore, we have the expression

$F \leq \mu mg$

Save your answers with

Gold Standard Education

Sign Up Now

Question 2: A brick is sliding down a rough plane inclined at $20°$ .

Given that its acceleration is $0.2\text{ ms}^{-2}$ , what is the coefficient of friction?

[4 marks]

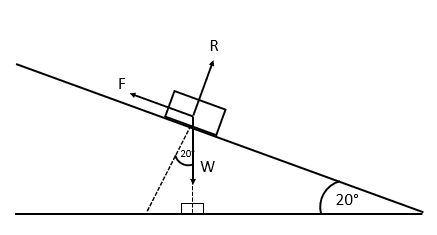
Resolving perpendicular to $F$ :

$R = W\cos 20° = mg\cos 20°$

Resolving parallel to $F$ :

Resultant Force = $F_{res} = ma = 0.2m$

We also have

$F_{res} = W\sin 20° - \mu R$

$= mg\sin 20° - \mu mg\cos 20°$

So,

$g\sin 20° - \mu g\cos 20° = 0.2$

Giving

$\mu = \dfrac{9.8\sin 20° - 0.2}{9.8\cos 20°} = 0.342\text{ (to }3\text{ dp)}$

Save your answers with

Gold Standard Education

Sign Up Now

Question 3: A $10\text{ g}$ particle travels along a flat surface at $80\text{ms}^{-1}$ . It slows to rest in $20\text{ seconds}$ . What is the coefficient of friction?

[4 marks]

For $v = u + at$ , we have