Forces
Forces Revision
Forces
For now, we’ll treat all objects in this section as particles. Essentially, we’re pretending that every object we look at is one-dimensional.
Forces to Know
There are a few different types of forces we’ll look at:
- Weight (W)
Weight always acts downwards, and is measured by multiplying mass, m, by the force of gravity, g, which you should be aware of from SUVAT.
- Normal Reaction (R)
The normal always acts perpendicular to the surface that our particle is resting on. For example, for a car parked on a hill, the normal reaction is exerted by the hill, pointing out towards the top of the car.
- Friction (F)
Friction is a resistance force calculated by the equation F \leq \mu R.\\ \mu is known as the coefficient of friction, and depends on the roughness between our particle and surface. Remember, friction always acts against motion.
- Thrust
Thrust is essentially force exerted by or on the particle. Imagine pushing a box up a hill – you are exerting thrust on the box.
- Tension (T)
Tension is similar to thrust in that it is resisted by friction, but requires a string, rope or wire that is taut (that is, at full extension).
All forces are measured in Newtons, N.
We’re also going to assume that air resistance and drag have no effect on the particle.
Note:
Forces that are perpendicular to each other have no effect on each other.
Take a box on a flat surface. Any kind of driving force to move the box forward (i.e. thrust, tension from a string) is not directly affected by the force of gravity, for example.
It may be indirectly affected, but we’ll get to that soon.
Terminology
First, some terminology.
- Particle – A body that takes up a point (i.e. its dimensions do not matter).
- Plane – A flat surface that the particle is acting on.
- Smooth – The plane offers no friction.
- Rough – The plane offers some friction, depending on \mu and R.
- Light – The particle has no mass.
- Resultant Force – The overall force when all components of force have been considered.
- Static – The particle is not moving.
- Equilibrium – The particle has no resultant force.
- Beam or Rod – A long particle (i.e. has a single length dimension which does matter).
- Uniform – The mass of a body is evenly spread across it.
- Non-Uniform – The mass of a body is not evenly spread.
- Rigid – The body does not bend.
- Thin – The body has no thickness (i.e. thickness does not matter).
- Inextensible – The body does not stretch when a force is applied to it.
S.I. Units
S.I. units are the standard system of measurements. There are three important base units that you should know.
Length: \text{metre (m)}
Time: \text{second (s)}
Mass: \text{kilogram (kg)}
Lots of other units are combinations of these three, these are called derived S.I. units. For example, velocity is measured in metres per second, which is \text{ms}^{-1}, so it is a derived S.I. unit as a combination of length and time.
Sometimes questions will ask about non-S.I. units, such as inches or miles per hour. All the information you need about these units will be given to you in the question.
Example 1: Simple Model
We have a box on a flat surface with someone pushing from one side, and someone pulling from the other side with a rope.
Friction opposes this motion.
Weight is counteracted by the reaction force.
Model this system.
[1 mark]
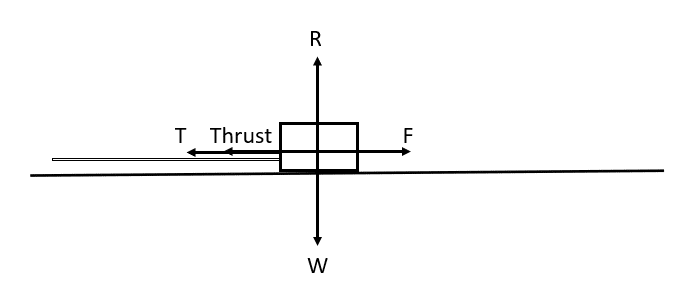
In these models, we vary the size of each arrow depending on the size of that force. For example, say the person pulling the rope applies double the force, then we would make the arrow twice as large. Assuming that friction is at its limit, we’d notice that the resultant force tends toward the left, and we’d see the box begin to accelerate in that direction.
Example 2: On a Tilted Plane
A car is driving up a hill, and being towed by a truck from the top of the hill.
Model this system, on the car only.
[2 marks]
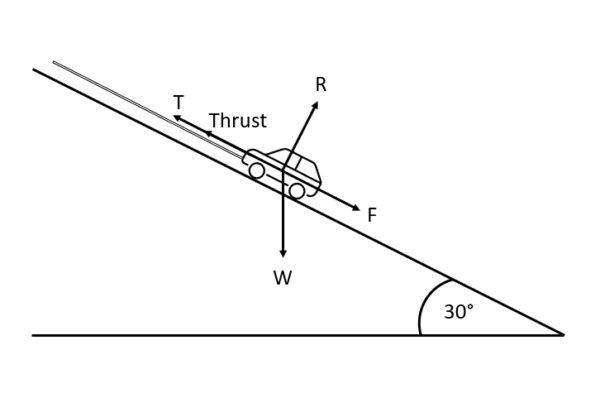
Thrust is provided by the car’s engine, and tension is provided by the rope from the tow truck.
Of course, friction is opposing this movement.
You’ll notice that the reaction force, R, is no longer acting vertically. However, it is perpendicular to the thrust, tension and friction, so it has no effect on how the car moves up the plane.
Let’s look at this problem in another way, now.
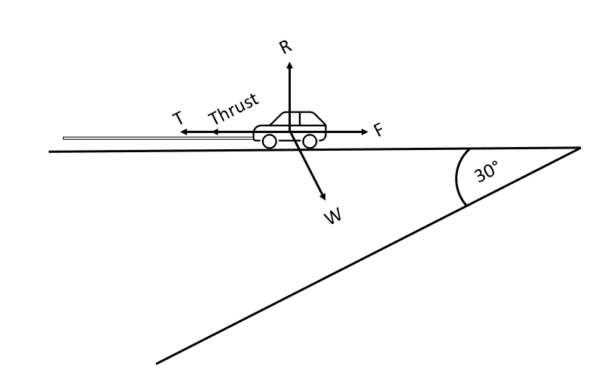
We can see that a component of the weight, W, is acting against the thrust and tension.
This means that the combined force of the thrust and tension must increase to counteract this change.
Forces Example Questions
Question 1: Here is a system where two balls are attached by a taut string. Given that Ball 2 (right) is twice as heavy as Ball 1 (left), what might we expect to see when we release both balls?
[1 mark]
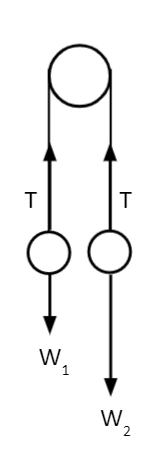
Given that the tension in the string is applied equally on both sides, we have the weight of one ball counteracting the other.
Since Ball 2 is twice as heavy, its downward force is twice as big. This means that Ball 1 is lifted up as a result.
Question 2: James is resting in a hammock, hanging by two ropes leading vertically.
Draw on the diagram the forces affecting this system.
[1 mark]
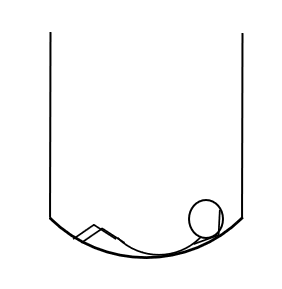
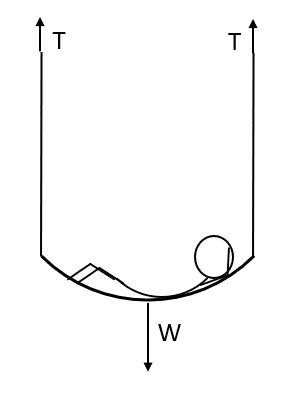
Question 3: Here is a system where two identical coins are balanced on a thin plank of wood, similar to a see-saw.
Say both coins are equidistant from the centre of the plank, what state might we say the system is in?
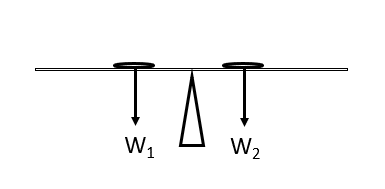
[1 mark]
The forces are equal on either side of the plank, so we see no movement, and claim the system is in equilibrium.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






