Revise
Projectiles
Projectiles Revision
Projectiles
We model projectile motion in two components, horizontal and vertical.
Make sure you are happy with the following topics before continuing.
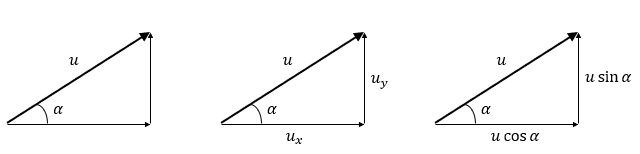
Splitting Velocity into Components
Using trigonometry, we convert a standard projectile motion into its two components.
Generally, we have a particle fired with a velocity u at an angle of \textcolor{orange}{\alpha}, which gives
Horizontal:
u\cos \textcolor{orange}{\alpha}
Vertical:
u\sin \textcolor{orange}{\alpha}
From here, we can use either method of modelling motion – SUVAT or integration/differentiation. We should use these piecewise, meaning, our equations in the vertical component are not the same equations in the horizontal component.
Finding a Maximum Height and Maximum Velocity
Remember, we can also find a maximum or minimum displacement by differentiating and finding the time \textcolor{purple}{t} where the velocity of our object is 0.
We can also find a maximum or minimum velocity by differentiating again and finding a time \textcolor{purple}{t} where the acceleration, \textcolor{blue}{a} = 0.
Example: Projectiles in Vector Notation
We can also use vectors to make projectile motion much neater.
So, for example, say a ball is thrown off of a cliff with a velocity of (15\textbf{i} + 7\textbf{j})\text{ ms}^{-1} with \textbf{i} its horizontal velocity, and \textbf{j} its upward vertical velocity. Assume that the ball accelerates due to gravity and experiences no air resistance. Given it is in the air for \textcolor{purple}{t} = \textcolor{purple}{5}\text{ seconds}, how tall is the cliff, what horizontal distance does the ball travel and what is its final velocity?
Assume g = 10\text{ ms}^{-2}.
[4 marks]
\textcolor{limegreen}{\underline{s}} = \underline{u}\textcolor{purple}{t} + \dfrac{1}{2}\textcolor{blue}{\underline{a}}\textcolor{purple}{t}^2
gives
\textcolor{limegreen}{\underline{s}} = \textcolor{purple}{5}(15\textbf{i} + 7\textbf{j}) + \dfrac{\textcolor{purple}{25}}{2}(\textcolor{blue}{-10\textbf{j}}) = \textcolor{limegreen}{75\textbf{i} - 90\textbf{j}}
So, the ball travels \textcolor{limegreen}{75}\text{ m} horizontally, and the cliff is \textcolor{limegreen}{90}\text{ m} tall.
\textcolor{red}{\underline{v}} = \underline{u} + \textcolor{blue}{\underline{a}}\textcolor{purple}{t}
gives
\textcolor{red}{\underline{v}} = (15\textbf{i} + 7\textbf{j}) - (\textcolor{blue}{10} \times \textcolor{purple}{5})\textbf{j} = \textcolor{red}{15\textbf{i} - 43\textbf{j}}\text{ ms}^{-1}
Projectiles Example Questions
Question 1: A particle is fired at a velocity of 5\text{ ms}^{-1} at an angle of 60°. What are the horizontal and vertical components of this velocity?
[2 marks]
\underline{u} = 5 gives
Horizontally:
5\cos 60° = 2.5\text{ ms}^{-1}
Vertically:
5\sin 60° = 4.33\text{ ms}^{-1}\text{ (to }2\text{ dp)}
Question 2: A football is kicked directly upwards with a velocity of 14.7\text{ ms}^{-1}. Show that the ball’s height exceeds 11\text{ m}, and that this maximum height occurs when t = 1.5\text{ seconds}.
Use the value g=9.8 \text{ ms}^{-1}
[2 marks]
Using
v = u + at
we have
0 = 14.7 - 9.8t
giving
t = 1.5\text{ seconds}
Substituting this into
s = ut + \dfrac{1}{2}at^2
we can prove that
\begin{aligned}s&=(14.7 \times 1.5) + \left( \dfrac{1}{2} \times -9.8 \times 1.5^2\right)\\[1.2em]&=11.025\text{ m}\end{aligned}
which is greater than 11\text{ m}, as required.
Question 3: A golf ball is hit with an initial velocity of (30\textbf{i} + 24.5\textbf{j})\text{ ms}^{-1}, where \textbf{i} represents the forward direction, and \textbf{j} represents upward vertical motion. Given that there is a constant headwind, impacting the ball’s acceleration by -2\text{ ms}^{-2}, and the ball lands 125\text{ m} from the tee, how long is it in flight for?
[5 marks]
\underline{u} = (30\textbf{i} + 24.5\textbf{j})
and
\underline{a} = (-2\textbf{i} - 9.8\textbf{j})\text{ ms}^{-2}
Using \underline{s} = \underline{u}t + \dfrac{1}{2}\underline{a}t^2 gives
125\textbf{i} = (30t\textbf{i} + 24.5t\textbf{j}) + (-t^2\textbf{i} - 4.9t^2\textbf{j})
Meaning
125 - 30t + t^2 = 0
and
24.5t - 4.9t^2 = 0
This gives t = 5\text{ seconds}.
