Newton's Laws
Newton's Laws Revision
Newton’s Laws
There are 3 Laws of Motion which are true for any system.
Make sure you are happy with the following topics before continuing.
Newton’s First Law
A body will maintain a constant velocity (including rest), unless an external force is applied to that body.
Newton’s Second Law
The resultant force on a body is equivalent to its mass, multiplied by its acceleration. Remember, the acceleration will be in the same direction as the resultant force. To be exact, we have the equation
F = ma
So, just as an example, in the Resolving Forces section, we’ve referenced the equation W = mg, relating weight to mass and the force of gravity. Weight is a force, and the value of g is given as 9.8\text{ ms}^{-2}, which is an acceleration.
Newton’s Third Law
When two bodies collide, they exert forces upon each other which are equal in magnitude but opposite in direction.
You might have heard the phrase, “every action has an equal and opposite reaction”. So, let’s say you lean against a wall. Since you are exerting a force on the wall, the wall exerts an equal force back on you.
Newton’s Laws in Vector Form
We can also apply F = ma to a system with multiple components, by applying the formula to each component separately.
Example: say a 4\text{ kg} particle is travelling with an acceleration \underline{a} = 2\textbf{i} + 3\textbf{j}.
Then its force F is given by F = 4(2\textbf{i} + 3\textbf{j}) = 8\textbf{i} + 12\textbf{j}.
A Level Maths Predicted Papers
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A Level Maths Revision Cards
The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. Maths Made Easy is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
Example 1: Rising and Falling Objects
A bag of mass 6\text{ kg} is picked up with a force of 90\text{ N}. Given that the only downward force is due to gravity, calculate its upward acceleration.
[2 marks]
First, we need to resolve our vertical forces. So, taking upwards to be the positive direction, we have
90 - (6 \times 9.8) = 31.2\text{ N}
Now, using Newton’s Second Law, F = ma, we have 31.2 = 6a. By extension, a = 5.2\text{ ms}^{-2}.
Example 2: Resolving in Perpendicular Directions
A particle is being pulled by a piece of string with a force of 17.32 \text{ N} at an angle of 30° to the horizontal. Given that there is no friction applied by the surface, and that the particle is accelerating horizontally at a rate of 3 \text{ ms}^{-2}, what is the mass of the particle? What is the reaction force R?
[4 marks]
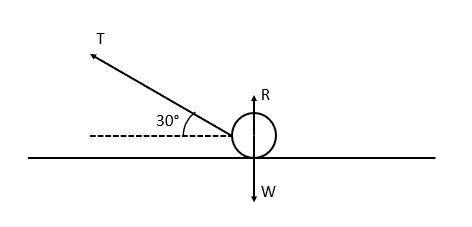
Resolving horizontally: T_H = 17.32\cos 30° = 15\text{ N}
Since we have F = ma, we have 15 = 3m, so the mass of the particle is 5\text{ kg}.
Now, resolving vertically: T_V + R = W, we have 17.32\sin 30° + R = 5 \times 9.8
Rearranging for R, we have R = 49 - 17.32\sin 30° = 40.34\text{ N}.
Newton's Laws Example Questions
Question 1: A 1.5\text{ kg} ball is falling with acceleration due to gravity.
What is the force acting upon it due to gravity?
After it has hit the ground, what is the reaction force R between it and the ground?
[2 marks]
Using Newton’s Second Law, we have F = 1.5 \times 9.8 = 14.7\text{ N}.
Using Newton’s Third Law, we must have R = W = 14.7\text{ N}.
Question 2: A 5\text{ kg} particle is travelling at 4.5\text{ ms}^{-1}. If a constant force of 0.1\text{ N} is applied to oppose its motion, how long does it take to stop?
[2 marks]
F = ma gives a = \dfrac{-0.1}{5} = -0.02\text{ ms}^{-2}
From here,
v = u + at gives 0 = 4.5 - 0.02t
Then, after rearranging,
t = \dfrac{4.5}{0.02} = 225\text{ s}
Question 3: A particle is decelerating, such that \underline{a} = \begin{pmatrix}-9\\ -3\end{pmatrix}. Given that its mass is 0.5\text{ kg}, what force is being applied to the particle?
[1 mark]
\underline{F} = m\underline{a}
Then,
\underline{F} = 0.5\begin{pmatrix}-9\\ -3\end{pmatrix} = \begin{pmatrix}-4.5\\ -1.5\end{pmatrix}
Newton's Laws Worksheet and Example Questions
SI Units
A LevelYou May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.