Moments
Moments Revision
Moments
For moments, we compare how a system might move in a clockwise or anticlockwise fashion around a pivot.
The Principles of Moments
Moments are quite simple to calculate. There are two things we need to know:
- Each body’s perpendicular distance from the point of rotation
- The force applied by each body
Imagine a seesaw with one child at either side.
If both children are sat as far from the centre as each other, but one child weighs more, the seesaw will lower on their side.
If both children weigh the same, but one child comes closer to the centre as the other stays in place, the seesaw will lower on the side of the furthest of the two.
Hence, the larger the force, and the greater the distance, the larger the moment.
Moments can be calculated by:
Moment = Force \times Perpendicular Distance from the force’s Line of Action
Weightless Beams
So, let’s say we’ve got a \color{limegreen}2\text{ m} long beam, balanced about its centre. We have a coin on one end of the beam, with a mass of \textcolor{purple}{10\text{ g}}. Assuming g = 10\text{ ms}^{-2}, how much downward force must we apply \textcolor{orange}{40\text{ cm}} away from the centre of the beam to keep the system in equilibrium?
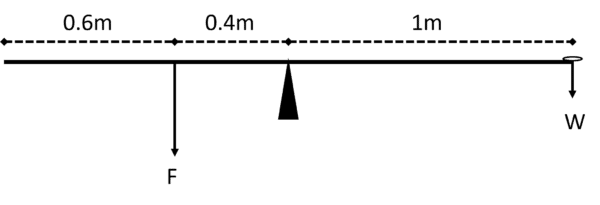
Let the coin be acting in a clockwise direction.
Clockwise moment: 1 \times \textcolor{purple}{0.01} \times 10 = 0.1\text{ Nm}
Anticlockwise moment: \textcolor{orange}{0.4} \times F = 0.1\text{ Nm}
This means that we require F = \dfrac{\textcolor{purple}{0.1}}{\textcolor{orange}{0.4}} = 0.25\text{ N}.
Uniform Rods
The previous example we assumed that the beam was weightless. While that does make our calculation easier, it isn’t quite right to use in a practical scenario.
Let’s now say that the beam is balanced \color{limegreen}1.5\text{ m} away from the coin, as below.
The beam now weighs \textcolor{blue}{20\text{ g}}. Assume, again that g = 10\text{ ms}^{-2} and that the system is in equilibrium.
We have to consider the centre of mass of the beam, as a new source of clockwise moments.
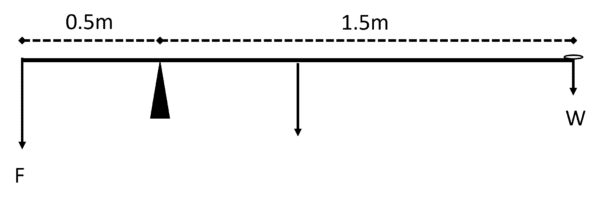
The beam’s centre of mass is \textcolor{orange}{0.5\text{ m}} away from the pivot.
Clockwise moment: (\textcolor{orange}{0.5} \times \textcolor{blue}{0.02} \times 10) + (\textcolor{limegreen}{1.5} \times \textcolor{purple}{0.01} \times 10) = 0.25\text{ Nm}
Anticlockwise moment: 0.5 \times F = 0.25\text{ Nm}
So we require F = \dfrac{0.25}{0.5} = 0.5\text{ N}.
Non-Uniform Rods
Let’s say the rod still weighs \textcolor{blue}{20\text{ g}}, but its centre of mass is no longer at the centre of the rod. Now, we exert a force of F = 0.58\text{ N}.
Given that the rod is still balanced \textcolor{limegreen}{1.5\text{ m}} away from the coin and the system is still in equilibrium, find out where the centre of mass of the rod lies.

Let x be the distance from the line of action.
Clockwise moment: (x \times \textcolor{blue}{0.02} \times 10) + (\textcolor{limegreen}{1.5} \times \textcolor{purple}{0.01} \times 10)
Anticlockwise moment: 0.5 \times 0.58 = 0.29\text{ Nm}
x = \dfrac{0.29 - (\textcolor{limegreen}{1.5} \times \textcolor{purple}{0.01} \times 10)}{(\textcolor{blue}{0.02} \times 10)} = 0.7\text{ m}.
Note:
It is sometimes possible that there are reactionary forces at the pivot. Don’t panic – this can be solved simply by resolving forces on the entire system.
Point of Tilting
Sometimes, a rod will rest on multiple supports. A rod is said to be at the point of tilting about a support if the reaction force at all other supports is 0. Even at the point of tilting, the rod is about to tilt rather than actually tilting, so moments are still balanced around the pivot.
Example: The rod below is at the point of tilting around support A. There are two weights attached to it, which are shown. One weight has a mass of \color{limegreen}2\color{grey}kg. Find the mass of the other weight, and the reaction force at support A.
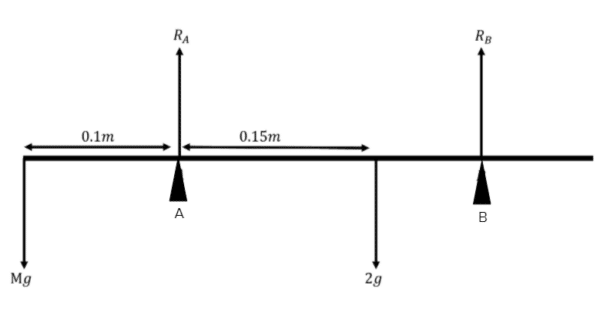
Since we are at the point of tilting about A, we know that R_{B}=0.
Take moments about A.
\color{orange}0.1\color{grey}Mg=\color{blue}0.15\color{grey}\times\color{limegreen}2\color{grey}g
0.98M=2.94
M=\dfrac{2.94}{0.98}
M=3
Resolve vertically:
R_{A}+R_{B}=Mg+\color{limegreen}2\color{grey}g
R_{B}=0
M=3
R_{A}=3g+\color{limegreen}2\color{grey}g
R_{A}=5g
R_{A}=49
Example: Angled Moments
One last thing – you might encounter some non-perpendicular forces being applied to the system too. You’ll need to recall the Resolving Forces section from before. Let’s say we have the same Weightless Beam system as in the previous examples, except we apply force F with a piece of string from below, at an angle of 45° to the horizontal.
Calculate the required force F, to keep the system in equilibrium.
[3 marks]
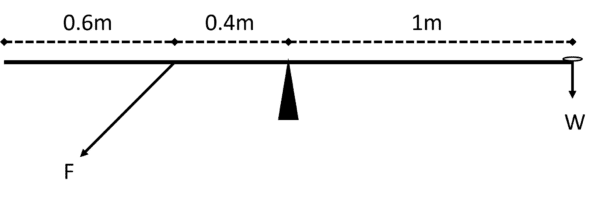
We then need to resolve the forces. Remember, the horizontal force applied by the string will not have an effect on the system as that component will not be perpendicular to the line of action. However, we have the vertical component, F\sin 45°, acting against the clockwise moment.
Clockwise moment: 1 \times 0.01 \times 10 = 0.1\text{ Nm}
Anticlockwise moment: 0.4 \times F\sin 45°
Then F =\dfrac{0.1}{0.4\sin 45°} = 0.35\text{ N (to }2\text{ dp)}.
Moments Example Questions
Question 1: Anna and Brandon are sat on a seesaw, pivoted at its centre. Given that Anna has a mass of 50\text{ kg} and is sat 1.25\text{ m} from the centre, and Brandon weighs 75\text{ kg}, how far away from the centre should Brandon sit to keep the seesaw in equilibrium?
Assume the seesaw is uniformly weighted.
[2 marks]
Let Anna provide anticlockwise motion and Brandon provide clockwise motion.
Anticlockwise: 50 \times 1.25 = 62.5\text{ Nm}
Clockwise: 75 \times x = 62.5\text{ Nm}
x = \dfrac{62.5}{75} = 0.83\text{ m (to }2\text{ dp)}
Question 2: An angular force of 96\text{ N} acts on a beam at an angle of 30\degree to the horizontal at a distance of 4\text{ m} away from the pivot. On the other side of the pivot, a vertical force acts 1\text{ m} away from the pivot. The system is in equilibrium. What is the magnitude of the vertical force?
[2 marks]
First draw a diagram.
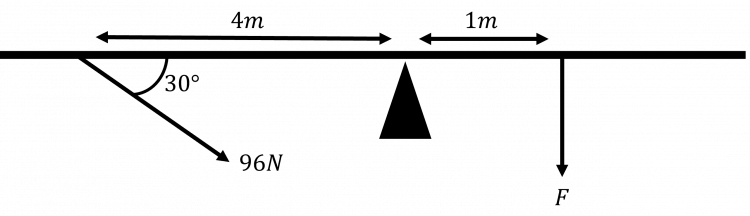
Since the 96\text{ N} force is at 30\degree, the vertical component is 96\sin(30)=48\text{ N}.
Take moments about the pivot:
48\times4=F\times1
F=192\text{ N}
Question 3: Find the value of F in this diagram, given that the pivot B is at the point of tilting.
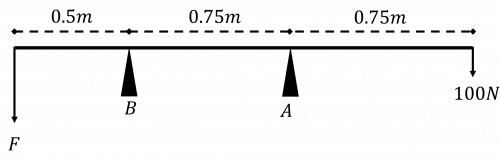
[2 marks]
At the point of tilting, the moments around the pivot are in equilibrium.
Since B is at the point of tilting, the reaction force at the pivot A must be 0, so we can ignore it in moment calculations.
Take moments about B:
0.5F=(0.75+0.75)\times100
0.5F=1.5\times100
0.5F=150
F=300\text{ N}







