Rate Equations
Rate Equations Revision
Rate Equations
The rate equation is the mathematical expression of the relationship between the rate of a chemical reaction and the concentrations of the substances involved in said reaction. The relationship between these variables is controlled by another variable known as the rate constant. The substances involved in chemical reactions will not affect the rate of that reaction in equal ways. We quantify the ways in which the concentration of a substance effects reaction rate using variables called rate orders.
The Rate Equation
The rate of a chemical reaction can be expressed using a fairly simple formula. This formula is known as the rate equation and it formalises the influence of reactant concentrations on the speed with which they react. For the general reaction:
\text{aW}+\text{bX}\rarr\text{cY}+\text{dZ}
The rate of reaction can be expressed, in terms of the concentrations of \text{W} and \text{X}, as:
\text{Rate}=\text{k[W]}^{\text{m}}\text{[X]}^{\text{n}}
The units of the rate are \text{mol dm}^{-3}\text{ s}^{-1}, the units for k however are variable and will depend on the values of m and n. The variables \text{m} and \text{n} are the orders of reaction with respect to species \text{W} and \text{X} respectively.
Reaction Orders
Reaction orders represent the effect that the concentration of a reactant has on the rate. Reactants that have a higher order associated with them will have a more significant effect on the reaction order.
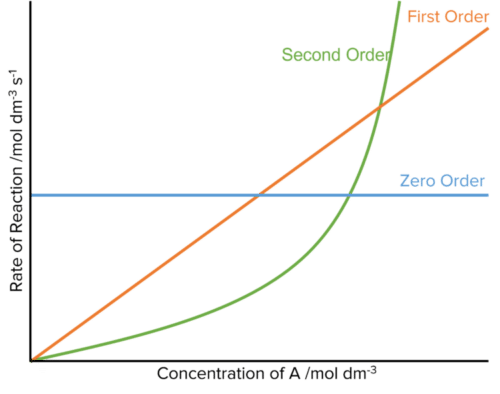
- Zero Order (\text{r} = \text{k[A]}^0): The concentration of A has no effect on the rate of reaction.
- First Order (\text{r} = \text{k[A]}^1): An increase in the concentration of A will cause a directly proportional increase in the rate of reaction
- Second Order (\text{r} = \text{k[A]}^2): An increase in the concentration of A will cause the rate of reaction to increase by the square of the concentration.
These influence of the reaction order on the rate of reaction can be seen in a when plotting a graph of reaction rate against the concentration of A.
The Rate Constant
The rate constant (also known as the rate coefficient) is usually represented by the letter \text{k} in the rate equation. Its value is not dependent on concentration or time and is constant at a specific temperature. The rate constant will change with temperature, e.g. if the temperature decreases, \text{k} also decreases.
The units for rate constant can be determined once the overall order of a reaction is known.
First Overall Order: \text{s}^{-1}
Second Overall Order: \text{mol}^{-1}\text{ dm}^3\text{ s}^{-1}
Third Overall Order: \text{mol}^{-2}\text{ dm}^6\text{ s}^{-1}
The units for the rate constant can also be deduced from the rate equation. If the rate equation is r = k[W]^1[X]^1 we could rearrange the equation to become:
\text{k}=\frac{\text{r}}{\text{[W]}^1\text{[X]}^1}
Then we can fill in the units we know in order to work out the units of the rate constant.
\text{k}=\frac{\text{mol dm}^{-3}\text{ s}^{-1}}{\text{[mol dm}^{-3}\text{][mol dm}^{-3}]}
Through cancelling down we can deduce that the units of \text{k} are:
\text{mol}^{-1}\text{ dm}^3\text{ s}^{-1}
Required Practical
Measuring the Continuous Rate of a Reaction
We can follow one experiment and record the change in concentration over time. This is known as the continuous rate method.
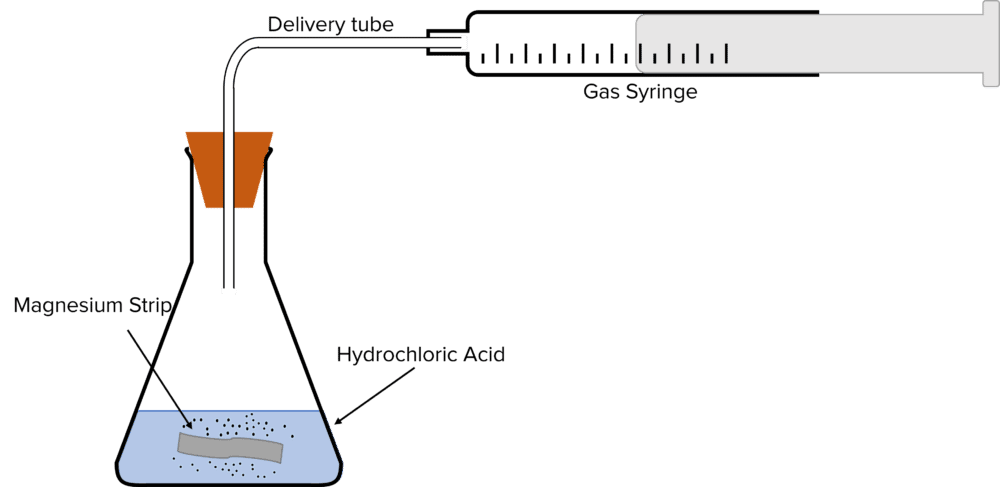
Method
- Measure 50\text{ cm}^3 of 1.0\text{ mol dm}^{-3} hydrochloric acid and add it to a conical flask.
- Set up a gas syringe and delivery tube to collect the gas evolved during the experiment.
- Weigh 0.25\text{ g} of magnesium ribbon.
- Add the magnesium ribbon to the conical flask and place the bung in the opening of the flask and begin timing.
- Every 15 seconds, record the volume of hydrogen gas collected. Do this for 3 minutes.
A gas syringe can be used to measure the continuous rate because there is a change in the number of moles of gas in the reaction. The rate at the start of a reaction is known as the initial rate, this is where the reaction is usually fastest.
Analysis
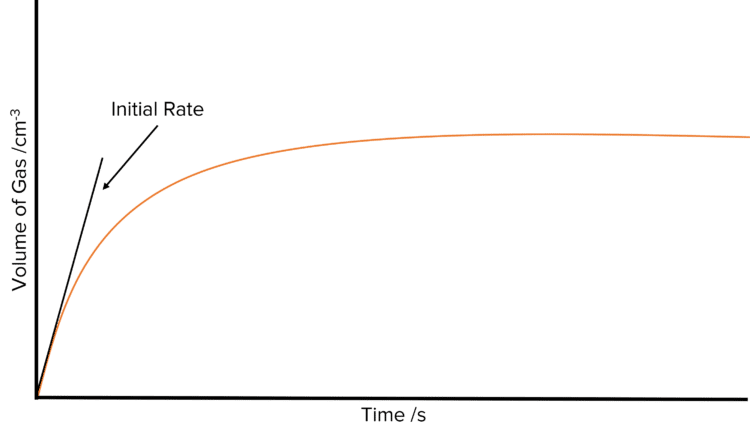
Once the experiment has been carried out, it is possible to calculate the initial rate of the reaction. First plot the volume of gas produced in the experiment against time. The curve should look rise sharply at first and then decline in gradient before plateauing at after a few minutes. Then draw a tangent to the curve starting from the origin. Find the gradient of this tangent to calculate the initial rate of the reaction.
Example: Calculating the Units of the Rate Constant
Write the rate equation for the reaction between A and B where A is second order and B is first order. Calculate the units for k.
[2 marks]
\text{r} = \text{k[A]}^2\text{[B]}^1
\begin{aligned}\text{k}&=\text{r[A]}^2\text{[B]}^1=\frac{\text{mol dm}^{-3}\text{ s}^{-1}}{\text{[mol dm}^{-3}\text{]}^2 \text{[mol dm}^{-3}\text{]}}\\ &=\textcolor{#008d65}{\text{mol}^{-2}\text{dm}^6\text{ s}^{-1}}\end{aligned}
Rate Equations Example Questions
Question 1: The following reaction takes place.
\text{H}_2 + \text{O}_2 \rarr\text{H}_2\text{O}
State the overall order for the reaction if the rate equation is r = k[H_2][O_2] and state the units for the rate constant.
[2 marks]
Overall order = 2
\text{mol}^{-1}\text{ dm}^3\text{ s}^{-1}
Question 2: The rate of the reaction between substance A and substance B was studied in a series of experiments carried out at the same temperature. In each experiment, the initial rate was measured using different concentrations of A and B. These results were used to deduce the order of reaction with respect to A and the order of reaction with respect to B.
What is meant by the term order of reaction with respect to A?
[1 mark]
Power to which the concentration term is raised in rate equation.
Question 3: When the concentrations of A and B were both doubled the initial rate increased by a factor of four. Deduce the overall order of the reaction.
[1 mark]
As doubling both reactant concentrations causes a quadrupling of the rate of reaction we can deduce that doubling a single concentration would double the rate of reaction. We can deduce that the reactants are both first order and so:
Overall Order: 2
Question 4: In an experiment, the concentration of A was increased by a factor of three and the concentration of B was halved. This caused the initial rate to increase by a factor of nine.
Deduce the order of reaction with respect to A and the order with respect to B.
[2 marks]
Order with Respect to A: 2
Order with Respect to B: 0
Question 5: Using your answers from question 4, write a rate equation for the reaction and suggest suitable units for the rate constant.
[2 marks]
Rate Equation: \text{Rate}=\text{k[A]}^2
Units: \text{mol}^{-1}\text{ dm}^3\text{ s}^{-1}
You May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
