The Arrhenius Equation
The Arrhenius Equation Revision
The Arrhenius Equation
The Arrhenius Equation provides a mathematical formula with which to investigate the relationship between the rate constant and temperature. The Arrhenius equation also introduces another constant known as the Arrhenius constant.
The Arrhenius Equation
Increasing the temperature of a reaction increases the value of the rate constant. The Arrhenius Equation shows the effect of temperature on the value of \text{k}.
\text{k}=\text{Ae}^{-\frac{\text{E}_a}{\text{RT}}}
If we inspect this equation, we see that it is mostly made up of constants, with \text{A} (the Arrhenius constant), \text{E}_{a} (activation energy), and \text{R} (the molar gas constant). We also see that the rate constant will increase exponentially with temperature. When plotted, this expression will yield a curve with a gradient gets increasingly steep as the temperature rises.
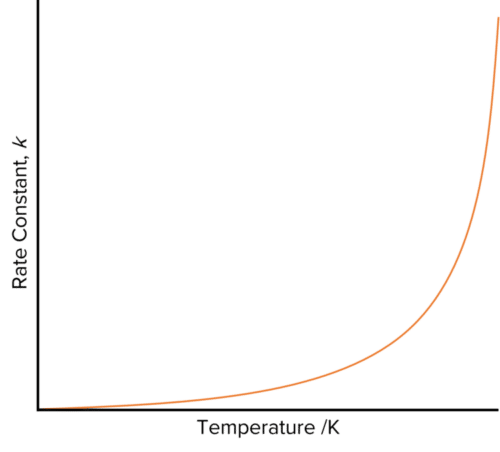
Though this curve demonstrates the relationship between the rate constant and temperature, it would not be easy to use it to find any of the constants contained with in the Arrhenius equation.
We can however rearrange the equation to put it into the form y=mx+c. To do this we take the natural logarithm of the equation. This will remove the exponential from the equation, and bring the -\frac{E_a}{RT} down:
\text{ln k}=\text{ln A}-\frac{\text{E}_a}{\text{RT}}
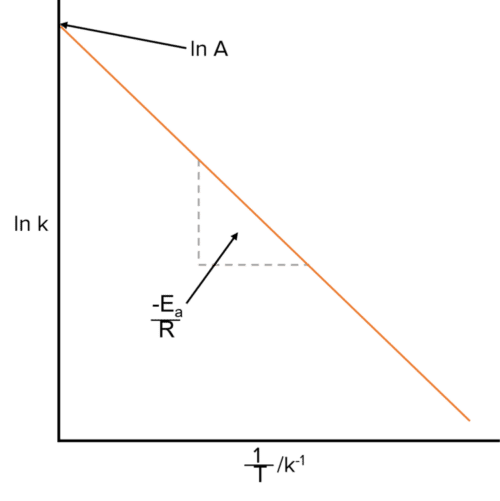
We can now plot a graph of ln k against \frac{1}{T}. This will produce a straight line with a slope equal to -\frac{E_a}{R}.
Example 1: Calculating The Arrhenius Constant
A reaction is carried out at \textcolor{#00bfa8}{30\degree \text{C}}. The value of \text{k} for the reaction is \textcolor{#f21cc2}{3.92\times 10^{-8}\text{s}^{-1}} and the activation energy is \textcolor{#a233ff}{89.9\text{ kJ mol}^{-1}}. The gas constant is \text{R} = 8.31\text{ J K}^{-1}\text{ mol}^{-1}.
Calculate the value for the Arrhenius Constant for the reaction.
[3 marks]
\begin{aligned}\text{k}&=\text{Ae}^{-\frac{\text{E}_a}{\text{RT}}}\\\text{}\\\text{A}&=\frac{\text{k}}{\text{e}^{-\frac{\text{E}_a}{\text{RT}}}}\\\text{}\\&=\frac{\textcolor{#f21cc2}{3.92\times 10^{-8}}}{\text{e}^{-\frac{\textcolor{#a233ff}{89900}}{8.31\times\textcolor{#00bfa8}{303}}}}\\\text{}\\ &=\textcolor{#008d65}{1.26 \times 10^8 \text{ s}^{-1}}\end{aligned}
Note: the units of the Arrhenius constant will always be the same as those of the rate constant. The exponential factor \left(\text{e}^{\frac{\text{E}_a}{\text{RT}}}\right) of the equation has no units as the units of activation energy, temperature and the gas constant are all the same.
Example 2: Graphical Calculations
Using the following data, determine the activation energy, in \text{kJ mol}^{-1}, and the value of \text{A}, given the following data.
| \text{T /}\degree \text{C} | \text{k /mol}^{-1}\text{ dm}^{3}\text{ s}^{-1} | \text{T /K} | \frac{1}{\text{T}}\text{ /k}^{-1} | ln k |
| 10 | 0.318 | |||
| 20 | 0.551 | |||
| 30 | 1.03 | |||
| 40 | 1.67 | |||
| 50 | 2.07 |
[12 marks]
Step 1: Complete the table.
| \text{T /}\degree \text{C} | \text{k /mol}^{-1}\text{ dm}^{3}\text{ s}^{-1} | \text{T /K} | \frac{1}{\text{T}}\text{ /k}^{-1} | \text{ln k} |
| 10 | 0.318 | 283 | 3.53 \times10^{-3} | -1.15 |
| 20 | 0.551 | 293 | 3.41\times10^{-3} | -0.596 |
| 30 | 1.03 | 303 | 3.30\times10^{-3} | 0.030 |
| 40 | 1.67 | 313 | 3.19\times10^{-3} | 0.513 |
| 50 | 2.07 | 323 | 3.10\times10^{-3} | 0.728 |
Step 2: Plot the Data.
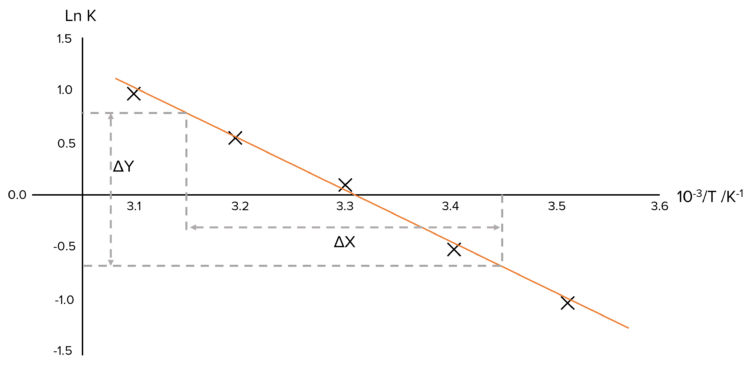
Step 3: Calculate the slope of the line.
\begin{aligned}\text{Slope}&=\frac{\Delta\text{Y}}{\Delta\text{X}}\\ &=\frac{0.75-(-0.30)}{3.45\times10^{-3}-3.15\times10^{-3}}\\ &=\textcolor{#008d65}{-3500\text{ K}}\end{aligned}
Step 4: Calculate \text{E}_a.
\begin{aligned}\text{Slope}&=\frac{-\text{E}_a}{\text{R}}\\ \text{E}_a &=-\text{Slope}\times\text{R}\\ &=-(-4350)\times8.31\\ &=\textcolor{#008d65}{29.1\text{ kJ mol}^{-1}}\end{aligned}
Step 4: Calculate the value of the Arrhenius constant.
\begin{aligned}\text{ln A} &= \text{y-intercept}\\\text{A}&=\text{e}^{\text{y-intercept}}\\ &=\text{e}^{14.6}\\ &=\textcolor{#008d65}{2.19\times10^{6}}\end{aligned}
The Arrhenius Equation Example Questions
Question 1: A reaction is carried out at 40\degree \text{C} The \text{k} value for the reaction is 4.10\times10^{-3}\text{ mol}^{-1}\text{ dm}^3\text{ s}^{-1}. The Arrhenius constant for the reaction is 1.20\times10^{7}. The gas constant is \text{R} = 8.31 \text{J K}^{-1}\text{ mol}^{-1}.
Calculate the value for the activation energy of the reaction.
[4 marks]
\text{ln k}=\text{ln A} - \frac{\text{E}_a}{\text{RT}} OR \text{E}_a=(\text{ln A} -\text{ln k})\times\text{RT}
\begin{aligned}\text{E}_a&=(\text{ln }1.20\times10^{7} -\text{ln } 4.10\times10^{-3})\times8.31\times313\\&=56.7\end{aligned}
\text{kJ mol}^{-1}
Question 2: A reaction is set up. The rate constant is found to be 2.2\times10^{-3}\text{ s}^{-1}. The Arrhenius constant for this reaction is 6.40\times10^{13}\text{ s}^{-1}. The activation energy is 100\text{ kJ mol}^{-1}. The gas constant is \text{R} = 8.31\text{ J K}^{-1}\text{ mol}^{-1}.
Calculate the temperature at which the reaction occurs.
[3 marks]
\text{ln k}=\text{ln A} -\frac{\text{E}_a}{\text{RT}} OR \text{T}=\frac{\text{E}_a}{\text{R}\times(\text{ln A}-\text{ln k})}
\begin{aligned}\text{T}&=\frac{100000}{(8.31\times\text{ln} 6.40\times10^{13}-\text{ln} 2.210\times10^{-3})}\\ &=317\text{K}\end{aligned}
Question 3: A student carries out an experiment. The results are recorded in Table 1.
| \text{T /}\degree \text{C} | \text{k /mol}^{-1}\text{ dm}^{3}\text{ s}^{-1} | \text{T /K} | \frac{1}{\text{T}}\text{ /k}^{-1} | \text{ln k} |
| 47 | 3.30\times10^{-4} | 320 | -8.02 | |
| 81 | 1.61\times10^{-3} | 354 | 2.82\times10^{-3} | |
| 108 | 4.00\times10^{-2} | 2.62\times10^{-3} | -3.22 | |
| 204 | 8.26\times10^{-1} | 447 | 2.10\times10^{-3} | |
| 300 | 7.56 | 537 | 1.75\times10^{-3} | 2.02 |
Calculate, using the data above, calculate the value of the activation energy for this reaction.
[9 marks]
Step 1: Complete the Table.
| \text{T /}\degree \text{C} | \text{k /mol}^{-1}\text{ dm}^{3}\text{ s}^{-1} | \text{T /K} | \frac{1}{\text{T}}\text{ /k}^{-1} | \text{ln k} |
| 47 | 3.30\times10^{-4} | 320 | \textcolor{#008d65}{3.13\times10^{-3}} | -8.02 |
| 81 | 1.61\times10^{-3} | 354 | 2.82\times10^{-3} | \textcolor{#008d65}{-6.43} |
| 108 | 4.00\times10^{-2} | \textcolor{#008d65}{381} | 2.62\times10^{-3} | -3.22 |
| 204 | 8.26\times10^{-1} | 447 | 2.10\times10^{-3} | \textcolor{#008d65}{-0.191} |
| 300 | 7.56 | 537 | 1.75\times10^{-3} | 2.02 |
Step 2: Plot the data.
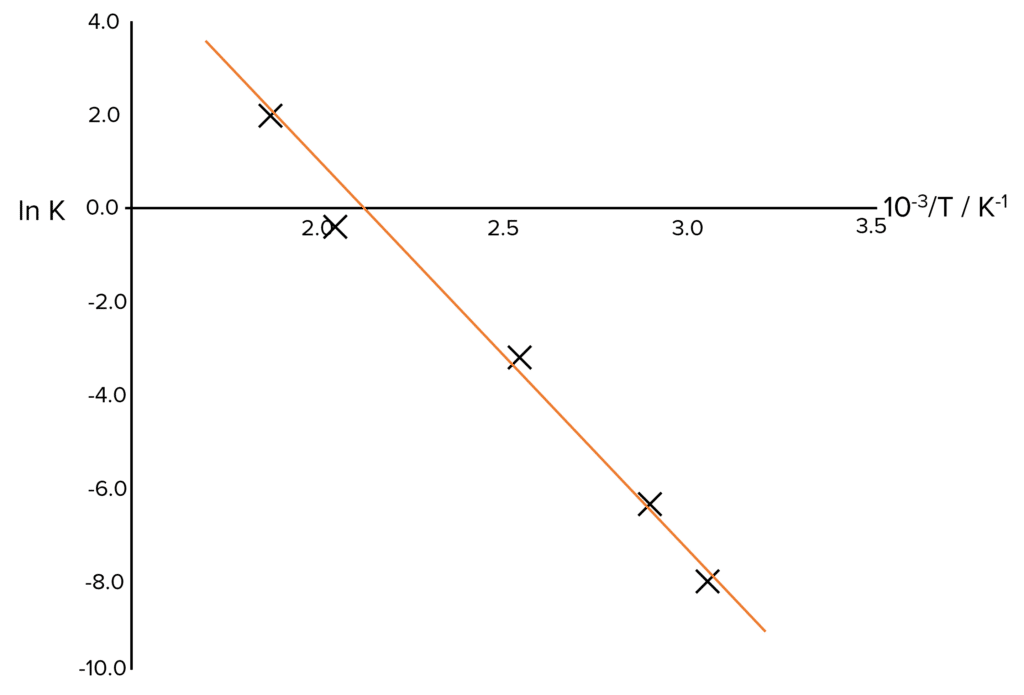
Step 3: Calculate the gradient of the graph.
\text{Gradient} = -7.44\times10^{-3}
(Accept any from -7.3\times10^{-3} to -7.6\times10^{-3})
Step 4: Calculate \text{E}_a.
\begin{aligned}\text{E}_a &= -7.44\times10^{-3} \times 8.31\\ &= 61.8\text{ kJ mol}^{-1}\end{aligned}
(Four marks for step 1, one mark per correctly calculated data. Two marks for step 2, allow both marks for correctly plotted graph from incorrect data. One Mark for step 3. Two marks for Step 4, one mark for correct calculation, one mark for correct answer.)
You May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
