Determination of Rate Equations & the Rate Determining Step
Determination of Rate Equations & the Rate Determining Step Revision
Determination of Rate Equations & the Rate Determining Step
Rate equations are determined experimentally by investigating the effect of changing concentrations and then deducing the order.
Using Initial Rate to Calculate Reaction Variables
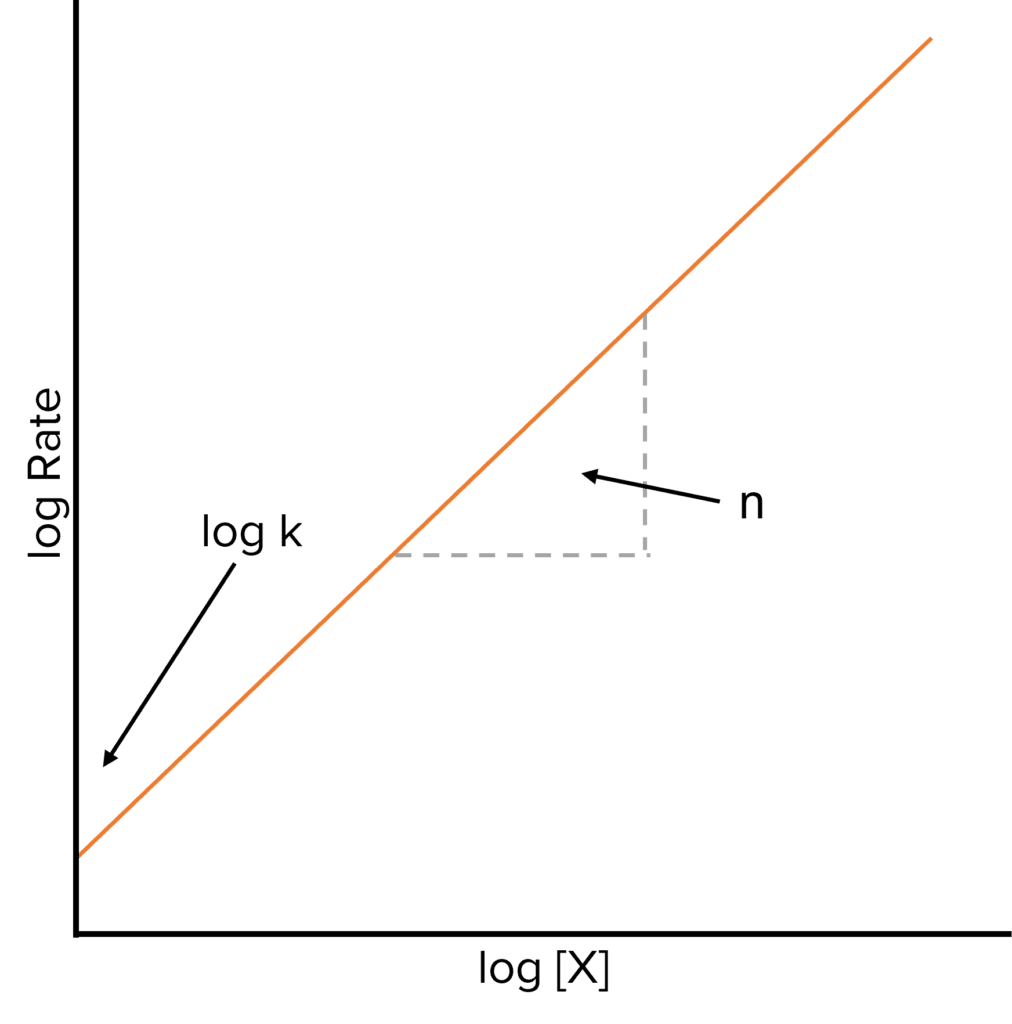

Rate equations have a general form:
\text{Rate} =k[X]^n
To work out the value of n graphically, we need to take logarithms of both sides of the equation to convert it to the form y = mx + c.
\text{log Rate}=\text{log k}+\text{n log [X]}
A graph of this equation would produce a straight line, where the \text{y-intercept} is equal to \text{log k} allowing us to calculate the rate constant \text{K}.
\text{K}=10^{\text{ y-intercept}}
The gradient of the line is equal to the order of reaction, \text{n}, with respect to X.
The Rate Determining Step
The slowest step in a reaction is known as the rate-determining step (RDS). It is rate-determining because it controls the overall rate of a reaction.
The rate equation contains species up to and including the rate-determining step. Therefore, we can use the rate equation to determine the rate-determining step. Take the reaction
\text{A} + 3\text{B} + 2\text{C} \rarr\text{D}
A suggested mechanism for this reaction is
Step 1: \text{A} + 2\text{B}\rarr\text{X}
Step 2: \text{B} + 2\text{C}\rarr\text{Y}
Step 3: \text{X} + \text{Y}\rarr\text{D}
The rate equation for the reaction is
\text{Rate} = \text{k[A][B]}^2
The rate equation tells us that there is 1 mole of A and 2 moles of B up to and including the rate-determining step. Step 1 contains both 1 mole of A, 2 moles of B, Step 2 contains only 1 mole of B and none of A, and Step 3 contains no moles of either species.
Step 3 cannot be the RDS as it does not contain either of the species contained in the rate equation. step 2 contains 1 mole of B, but taking both steps 1 and 2 together gives 3 moles of B in total. As the rate equation contains only 2 moles of B step 3 can’t be the RDS. Step 1 contains the correct number of both moles according to the rate equation and so must be the rate determining step.
Determining Reaction Orders From Experimental Data.
By carrying out a series of experiments using different concentrations of reactants, we can determine the rate equation of a reaction. To do this we need to compare the effects of the different concentrations on the initial rate.
| Experiment | Initial Concentration of X /\text{mol dm}^{-3} | Initial Concentration of Y /\text{mol dm}^{-3} | Initial Rate /\text{mol dm}^{-3}\text{ s}^{-1} |
| 1 | 0.12 | 0.26 | 2.10\times10^{-4} |
| 2 | 0.36 | 0.26 | 1.98\times10^{-3} |
| 3 | 0.72 | 0.13 | 3.78\times10^{-3} |
[5 marks]
We can start by comparing the rates of experiments 1 and 2. Although the concentration of Y remains constant, the initial rate changes. That immediately tells us that the order of X is greater than 0 and is part of the rate equation.
From experiments 1 to 2, the concentration of X triples while the initial rate increases by a factor of 9. This means that the order of X must be 2 (you can work out the amount the initial rate increases if you divide the rates).
\text{Rate} = \text{k[X]}^2
We can now look at experiments 2 and 3 to find the effect of Y. Firstly, we have to consider the effect of X. Between experiments 2 and 3, the concentration of X doubles. We know that X is second order so from experiments 2 to 3, the initial rate would be expected to quadruple from 1.8\times10^{-3}\text{ mol dm}^{-3}\text{ s}^{-1} to 7.56\times10^{-3}\text{ mol dm}^{-3}\text{ s}^{-1}.
Since that is not the initial rate of the reaction, Y must have an order greater than 0. From experiments 2 to 3, the concentration of Y halves, meanwhile, the rate is half the expected value of 7.56\times10^{-3}\text{ mol dm}^{-3}\text{ s}^{-1}, so Y must be first order.
\text{Rate} = \text{k[X]}^2\text{[Y]}
To calculate the value for \text{k}, the rate equation needs to be rearranged to make \text{k} the subject, and then the known values can be substituted into the equation.
For example, if we use the rate equation above, \text{Rate} = k [X]^2[Y], we can find \text{k} using the equation k=\frac{\text{Rate}}{[X]^2[Y]}.
Required Practical
Initial Rate Experiments – The Iodine Clock
The initial rate of a reaction can be calculated by carrying out a clock reaction. In clock reaction, a system is designed so that it can be monitored over a set period of time or until one product has been produced in a specific concentration.
Method
In this common clock reaction, hydrogen peroxide (\text{H}_2\text{O}_2), iodide ions (\text{I}^-), thiosulfate ions (\text{S}_2\text{O}_3^{2-}) and starch are mixed together. The following reactions take place:
\text{H}_2\text{O}_{\text{2(l)}} + 2\text{H}^+_{\text{(aq)}} + 2\text{I}^{-}_{\text{(aq)}} \rarr \text{I}_{\text{2 (aq)}}
2\text{S}_2\text{O}_3^{2-}\text{}_{\text{(aq)}}+\text{I}_{\text{2(aq)}}\rarr2\text{I}^-_{\text{(aq)}}+\text{S}_4\text{O}_6^{2-}\text{}_{\text{(aq)}}
- Fill a burette (50\text{ cm}^3) with potassium iodide solution. Rinse the 50\text{ cm}^3 burette with potassium iodide beforehand to improve accuracy.
- Put 10.0\text{ cm}^3 of hydrogen peroxide into a clean and dry measuring cylinder.
- Use a measuring cylinder to add 25\text{ cm}^3 of sulfuric acid to a second 250\text{ cm}^3 beaker. Then, add 20\text{ cm}^3 of deionised water into the beaker.
- Use a plastic dropping pipette to add about 1\text{ cm}^3 of starch solution to the 250\text{ cm}^3 beaker.
- Use the burette to add 5.0\text{ cm}^3 of potassium iodide solution to the mixture in the 250\text{ cm}^3 beaker.
- Finally add 5.0\text{ cm}^3 of sodium thiosulfate solution to the mixture in the 250\text{ cm}^3 beaker.
- Stir the mixture in the 250\text{ cm}^3 beaker and pour the 10.0\text{ cm}^3 hydrogen peroxide solution from the measuring cylinder into the 250\text{ cm}^3 beaker and immediately start the timer.
- Stop the timer when the mixture in the 250\text{ cm}^3 beaker turns blue-black and record the time.
- Repeat steps 1-8 at least two more times, changing the potassium iodide concentration each time. This is to allow the order of reaction to be determined.
- Plot a graph of initial rate versus concentration to determine the order.
Determination of Rate Equations & the Rate Determining Step Example Questions
Question 1: The overall equation for a reaction is as follows.
\text{NO}_{2\text{(g)}} + \text{CO}_{\text{(g)}} \rarr \text{NO}_{\text{(g)}} + \text{CO}_{2\text{(g)}}
Below is the mechanism for the reaction.
Step 1:
Step 2:
\text{NO}_3+\text{CO}\rarr\text{NO}_2+\text{CO}_2
Step 1 is the slowest step in the reaction. Determine the rate equation for the reaction. Explain your answer.
[2 marks]
\text{Rate} = \text{k[NO}_2\text{]}^2.
\text{NO}_2 appears twice in the rate-determining step while \text{CO} does not appear at all.
Question 2: When placed in a dilute alkaline solution, ethanal undergoes the following reaction.
2\text{CH}_3\text{CHO}\rarr \text{CH}_3\text{CH(OH)CH}_2\text{CHO}
Below is the rate equation of the reaction.
\text{Rate} = \text{k}\left[\text{CH}_3\text{CHO}\right]\left[\text{OH}^\text{-}\right]
The initial rate of the reaction is found to be 2.5\times10^{-3}\text{ mol dm}^{-3}\text{ s}^{-1} when the initial concentration of ethanal is 0.15\text{ mol dm}^{-3}, and the initial concentration of sodium hydroxide is 0.030\text{ mol dm}^{-3}.
Calculate the value for the rate constant at this temperature and give its units.
[3 marks]
\begin{aligned}\text{k}&=\frac{2.5\times10^{-3}}{0.15\times0.03}\\ &=0.555\end{aligned}
Units:\text{ mol}^{-1}\text{dm}^{3}\text{ s}^{-1}
Question 3: The data in the following table was obtained by carrying out a series of experiments to find the initial rate of reaction between substances X and Y.
| Experiment | Initial Concentration of X /\text{mol dm}^{-3} | Initial Concentration of Y /\text{mol dm}^{-3} | Initial Rate /\text{mol dm}^{-3}\text{ s}^{-1} |
| 1 | 0.14 | 0.24 | 2.60\times10^{-4} |
| 2 | 0.42 | 0.24 | 2.34\times10^{-3} |
| 3 | 0.84 | 0.48 | 9.36\times10^{-3} |
Deduce the orders of the reaction with respect to X and Y.
[2 marks]
Order with respect to X: 2 or \text{[X]}^2
Order with respect to Y: 0 or \text{[Y]}^0
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.