Entropy & Gibbs Free-Energy
Entropy & Gibbs Free-Energy Revision
Entropy & Gibbs Free Energy
Entropy is an extremely important variable in chemistry. When coupled with the Gibbs Free energy, entropy will determine whether or not a reaction can take place.
Entropy
Entropy, \text{S}, is a measure of the number of different ways in which a system can be arranged. In simple terms, it is a measure of disorder with in a system. If there are many ways of arranging the atoms or particles in a system then the system is disordered and the entropy is high.
The entropy of a system is increased by increasing the ways in which its constituents can be arranged. In practice this means that systems where the particles are able to move more freely (e.g. liquids or gasses) have a much higher entropy than ones in which the particles are strongly constrained (e.g. solids).
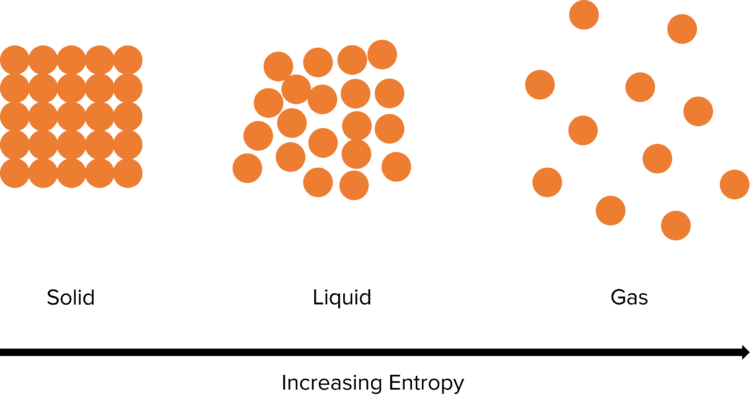
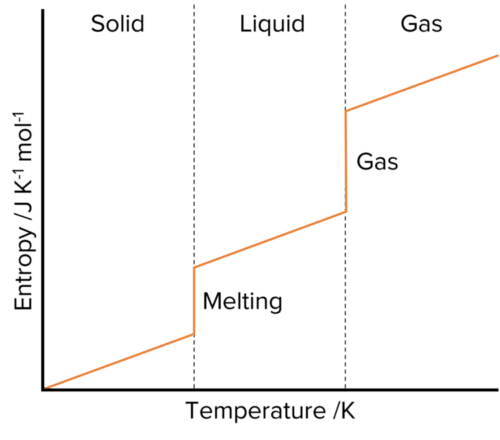
The entropy of a system also increases as its temperature increases. As the system gains more energy, the movement of the particles within it increases, creating more disorder and hence raising the entropy. When substances go through changes in state (such as melting or boiling) there is always a rapid change in entropy. This is because the disorder in a system rapidly changes.
Consider a system in which a solid substance is heated up to melting point. The particles in the system will gain more and more freedom as the substance heats up, but will remain fixed in the solid structure. This will lead to a gradual increase in the systems entropy. At a certain temperature however, the solid will melt, freeing the particles into liquid phase. This sudden increase in disorder leads to a jump in the entropy of the system.
Increasing the number of particles present in a system will also increase its entropy. Take for example the thermal decomposition of calcium carbonate (\text{CaCO}_3):
\text{CaCO}_3\rarr\text{CaO}+\text{CO}_2
Here the system moves from one particle on the left to two on the right. This will double the number of ways in which the system can be arranged, increasing the entropy.
A number of other factors will also increase entropy, such as the purity, complexity, and constituents of a compound.
| Pure Substances | usually have a lower entropy than | Mixtures |
| Elements | Compounds | |
| Simple Compounds | Complex Compounds |
During chemical reactions there is often a change in entropy (\Delta\text{S}) as there will be a difference the entropies of the products and of the reactants. This change in entropy is calculated using the following equation:
\Delta_{\text{r}}\text{S /J K}^{-1}\text{ mol}^{-1}=\Sigma(\text{S}_{\text{products}})-\Sigma(\text{S}_{\text{reactants}})
Gibbs Free Energy Change
The Gibbs Free-Energy, \Delta\text{G} combines the effect of enthalpy, temperature and entropy to determine if a reaction is feasible (i.e. whether it is theoretically possible). Reactions that are feasible at a given temperature are said to be spontaneous at that temperature. A spontaneous reaction is one which happens with no external influence. If the Gibbs Free-Energy of a reaction is greater than 0 (i.e positive), the reaction will not happen spontaneously. If it is less than 0 (i.e negative), the reaction will happen spontaneously. The Gibbs free energy is calculated using the following equation:
\Delta\text{G}=\Delta\text{H}-\text{T}\Delta\text{S}
The existence of \Delta\text{S} is key to the explanation of feasibility. Without this term, \Delta\text{G} would always be negative and hence all reactions feasible. As this is not the case, it must be concluded that \Delta\text{H} alone is not a sufficient explanation.
It is important to note that a reaction can have a negative \Delta\text{G} and still not occur since the reaction may be so slow that it can be said to not be happening at all. Reactions may also feasible but not physically possible, for example, aqueous reactions that take place above the boiling point of water.
Gibbs Free Energy Graphs
The equation for Gibbs Free-Energy is of the form y = mx + c:
\begin{aligned}\text{y}&=\text{c}+\text{mx}\\ \Delta\text{G}&=\Delta\text{H}-T\Delta\text{S}\end{aligned}
This means that the relationship between the Gibbs Free-Energy of a reaction and its temperature can be represented using a straight line graph of \Delta\text{G} against T. Below is an example of this for a reaction with a negative \Delta\text{S}.
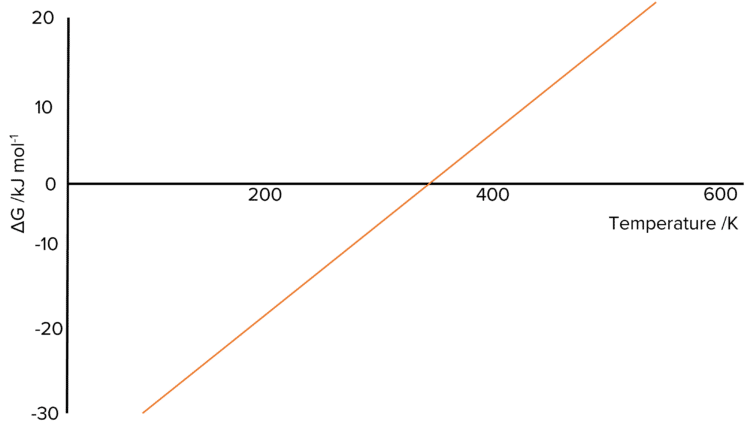
A number of quantities can be read off using these graphs:
- The value \text{y-intercept (c)} of the graph is equal to the value of the enthalpy change, \Delta\text{H}, of the reaction \left(\text{c}=\Delta\text{H}\right).
- The value of the \text{slope (m)} of the graph is equal to the negative value of the entropy change, \Delta\text{S} of the reaction. This means we can calulate \Delta\text{S} by taking the negative of the gradient \left(-\text{m}=\Delta\text{S}\right).
- The point where the line crosses the x-axis is where the reaction becomes feasible since Gibbs Free-Energy is less than 0.
Effect of Temperature on Feasibility
The feasibility of a reaction will change depending on the temperature and the type of reaction. The table shows the effect of \Delta\text{H}, \Delta\text{S}, and temperature on the feasibility of a reaction.
\Delta\text{G}=\Delta\text{H}-\text{T}\Delta\text{S}
| \Delta\text{H} | \Delta\text{S} | \Delta\text{G} | Feasibility |
| Positive | Positive | Can be positive or negative. Decreases with temperature. | Will become feasible above a certain temperature. |
| Positive | Negative | Positive at all temperatures. | Never |
| Negative | Positive | Negative at all temperatures. | Always |
| Negative | Negative | Can be positive or negative. Increases with temperature. | Will become feasible below a certain temperature. |
For example, if a reaction had a negative value of \Delta\text{H} and a positive value of \Delta\text{S} the \Delta\text{G} will always be 0. This is because the term \text{T}\Delta\text{S} will always be negative. As \Delta\text{H} is negative, subtracting the positive value of \text{T}\Delta\text{S} will always be less than 0
Example 1: Calculating Enthalpy Changes
The reaction below only becomes feasible at temperatures above 5445K.
\text{H}_2\text{O}\rarr\text{H}_2+\frac{1}{2}\text{O}_2
The entropies of the species above are shown in the table below.
| \text{H}_2\text{O} | \text{H}_2 | \text{O}_2 | |
| \text{S /kJ mol}^{-1} | 192 | 128 | 203 |
Calculate the entropy change, S, for this reaction.
[2 marks]
\begin{aligned}\Delta_{\text{r}}\text{S}&=\Sigma(\text{S}_{\text{products}})-\Sigma(\text{S}_{\text{reactants}})\\ &=[128+(0.5 \times 203)]-192\\ &=\textcolor{#008d65}{37.5\text{ kJ mol}^{-1}}\end{aligned}
Example 2: Calculations Using the Gibbs Free Energy
The table below contains thermodynamic data for hydrogen, oxygen and water.
| \text{S}^{\varnothing}\text{ /J K}^{-1}\text{ mol}^{-1} | \Delta_{\text{f}}\text{H}^{\varnothing}\text{ /kJ mol}^{-1} | |
| \text{H}_{2 (g)} | 130 | 0 |
| \text{O}_{\text{2 (g)}} | 200 | 0 |
| \text{H}_2\text{O}_{\text{(g)}} | 192 | -240 |
Calculate the temperature above which the reaction between hydrogen and oxygen to form gaseous water is not feasible.
[3 marks]
Step 1: Write the equation for the reaction.
\text{H}_{\text{2 (g)}}+\frac{1}{2}\text{O}_{\text{2 (g)}}\rarr\text{H}_2\text{O}_{\text{(g)}}
Step 2: Set \Delta\text{G} to 0.
For a reaction to not be feasible, the value for Gibbs Free Energy must be greater than 0. So, we can set the value for Gibbs Free Energy as 0.
\Delta\text{G}=\Delta\text{H}-T\Delta\text{S}=0
Now we can make the temperature the subject and solve the equation. We have to ensure that the units are the same for enthalpy and entropy.
Step 3: Make temperature (T) the subject of the equation.
\begin{aligned}0&=\Delta\text{H}-T\Delta\text{S}\\T&=\frac{\Delta\text{H}}{\Delta\text{S}}\end{aligned}
Step 4: Calculate the temperature at which the reaction becomes feasible.
\begin{aligned}T&=\frac{\Delta\text{H}}{\Delta\text{S}}\\ &=\frac{(-240)\times1000}{192-\left(130+\frac{200}{2}\right)}\\ &=\textcolor{#008d65}{6316\text{K}}\end{aligned}
Entropy & Gibbs Free-Energy Example Questions
Question 1: Explain why water evaporation is spontaneous even though the change is endothermic. In your answer, make sure to refer to the change in the arrangement of water molecules and the entropy change.
[4 marks]
- The molecules of water become more disordered (/ random) when water evaporates(/ changes from a liquid to a gas).
- Therefore the entropy is positive OR entropy increases.
- Since the entropy increases, \text{T}\Delta\text{S} is greater than \Delta\text{H}
- So \Delta\text{G}<0
Question 2: The figure below shows how the entropy of a molecular substance Y varies with temperature.
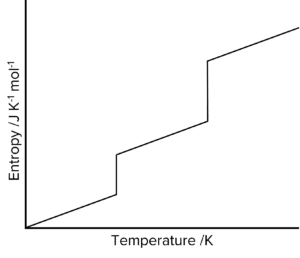
Explain, in terms of molecules, why the entropy is zero when the temperature is zero Kelvin.
[2 marks]
- At 0\text{K} the particles are stationary (/ not vibrating) and would have zero energy
- So there is no disorder (/ perfect order/ maximum order).
Question 3: The image below shows how the free-energy change for a particular gas-phase reaction varies with temperature.
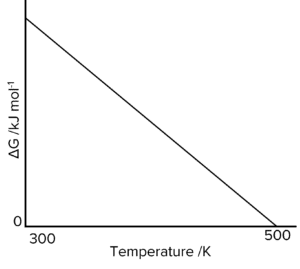
Explain, using a thermodynamic equation, why this line follows the mathematical equation for a straight line, \text{y} = \text{mx} + \text{c}. Explain why the magnitude of \Delta\text{G} decreases as \text{T} increases in this reaction.
[2 marks]
\Delta\text{G}=\Delta\text{H}-T\Delta\text{S}
\begin{aligned}\Delta\text{H} &= \text{c}\\-\Delta\text{S} &= \text{m}\end{aligned}
Because the entropy change is positive OR {\text{T}\Delta\text{S}} gets bigger OR {-\text{T}\Delta\text{S}} gets more negative.
Question 4: The reaction below can lead to the release of nitrogen monoxide into the atmosphere.
\frac{1}{2}\text{N}_{\text{2 (g)}}+\frac{1}{2}\text{O}_{\text{2 (g)}}\rarr\text{NO}_{\text{(g)}}
Use the data from the table to calculate the minimum temperature above which the reaction is feasible.
| \text{S}^{\varnothing}\text{ /J K}^{-1}\text{ mol}^{-1} | \Delta_{\text{f}}\text{H}^{\varnothing}\text{ /kJ mol}^{-1} | |
| \text{N}_{2\text{(g)}} | 192.2 | 0 |
| \text{O}_{2\text{(g)}} | 205.3 | 0 |
| \text{NO}_{\text{(g)}} | 211.1 | +90.4 |
[5 marks]
Step 1: Obtain an expression for \text{T}.
When \Delta\text{G} = 0\text{, T}=\frac{\Delta\text{H}}{\Delta\text{S}}
Step 2: Calculate \Delta\text{H}.
\Delta\text{H} = +90.4\text{ kJ mol}^{-1}
Step 3: Calculate \Delta\text{S}.
\begin{aligned}\Delta_{\text{r}}\text{S}&=\Sigma(\text{S}_{\text{products}})-\Sigma(\text{S}_{\text{reactants}})\\ &= 211.1 - \left(\frac{205.3}{2}\right) - \left(\frac{192.2}{2}\right)\\ &= 12.35\end{aligned}
Step 4: Calculate \text{T}.
\text{T}=\frac{90.4\times 1000}{12.35} = 7320\text{K}
(One mark for Steps 1, 2, & 4. Two marks for Step 3. Allow \text{T} in the range 7230-7350)
Question 5: The following reaction between iron (III) oxide and carbon monoxide takes place.
\text{Fe}_2\text{O}_{\text{3 (s)}} + 3\text{CO}_{\text{(g)}} \rarr 2\text{Fe}_{\text{(s)}} + 3\text{CO}_{2\text{(g)}}
Calculate the standard entropy change for this reaction using the information in the table.
| \Delta\text{S}^{\varnothing}\text{/J K}^{-1}\text{ mol}^{-1} | |
| \text{Fe}_2\text{O}_{\text{3 (s)}} | 87.6 |
| \text{Fe}_{\text{(s)}} | 25.2 |
| \text{CO}_{\text{(s)}} | 199.1 |
| \text{CO}_{\text{2 (g)}} | 213 |
[4 marks]
\begin{aligned}\Delta_{\text{r}}\text{S}&=\Sigma(\text{S}_{\text{products}})-\Sigma(\text{S}_{\text{reactants}})\\&= [(2 \times 25.2) + (3\times 213)] - ]87.6 + (3 \times 199.1)]\\ &=689.4 - 684.9\\ &= 4.5\text{J K}^{-1}\text{ mol}^{-1}\end{aligned}
(One mark per correct line of working}
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.