Born - Haber Cycles
Born - Haber Cycles Revision
Born-Haber Cycles
A Born-Haber Cycle is an application of the Hess cycle. It is a cycle that includes every enthalpy change that is involved in the formation of ionic compounds.
Enthalpies
Enthalpy of Formation
The enthalpy of formation \left(\Delta_{\text{f}}\text{H}^{\varnothing}\right), is the enthalpy change when one mole of a compound is formed from its constituent elements under standard conditions with all reactants and products being in their standard states.
\text{Na}_{\text{(s)}}+\frac{1}{2}\text{Cl}_{2\text{(g)}}\rarr\text{NaCl}_{\text{(s)}}
Ionisation Enthalpy
First Ionisation Enthalpy \left(\Delta_{\text{ie 1}}\text{H}^{\varnothing}\right):
The first ionisation enthalpy is the enthalpy change needed to remove one mole of electrons from one mole of gaseous atoms to form one mole of gaseous ions with a +1 charge.
\text{X}_{\text{(g)}}\rarr\text{X}^+_{\text{(g)}}+\text{e}^-
Second Ionisation Enthalpy \left(\Delta_{\text{ie 2}}\text{H}^{\varnothing}\right):
The second ionisation enthalpy is the enthalpy change needed to remove one mole of electrons from one mole of gaseous +1 ions to form one mole of gaseous ions with a +2 charge.
\text{X}^+_{\text{(g)}}\rarr\text{X}^{2+}_{\text{(g)}}+\text{e}^-
Enthalpy of Atomisation
The enthalpy of atomisation of an element \left(\Delta_{\text{at}}\text{H}^{\varnothing}\right), is the enthalpy change when one mole of gaseous atoms is formed from the element in its standard state.
\text{X}_{\text{(s)}}\rarr\text{X}_{\text{(g)}}
Bond Dissociation Enthalpy
The bond dissociation enthalpy \left(\Delta\text{diss}\text{H}^{\varnothing}\right), is the standard enthalpy change when one mole of a covalent bond is broken to create two gaseous atoms or free radicals.
\text{X}_{2\text{(s)}}\rarr 2\text{X}_{\text{(g)}}
Electron Affinity
First Electron Affinity \left(\Delta_{\text{ea 1}}\text{H}^{\varnothing}\right):
The first electron affinity is the enthalpy change when one mole of gaseous atoms gains one mole of electrons to form one mole of gaseous ions with a -1 charge.
This is an exothermic process for atoms that usually form negative ions. The ions formed are more stable than the atoms.
\text{X}_{\text{(g)}}+\text{e}^-\rarr\text{X}^-_{\text{(g)}}
Second Electron Affinity \left(\Delta_{\text{ea 2}}\text{H}^{\varnothing}\right):
The second electron affinity is the enthalpy change when one mole of gaseous -1 ions gains one mole of electrons to form one mole of gaseous ions with a -2 charge.
This is an endothermic process. This is because energy is required to overcome repulsion between negative ions and the electrons.
\text{X}^-_{\text{(g)}}\rarr\text{X}^{2-}_{\text{(g)}}+\text{e}^-
Enthalpy of Hydration
The enthalpy of hydration \left(\Delta_{\text{hyd}}\text{H}^{\varnothing}\right), is the enthalpy change when one mole of gaseous ions forms one mole of aqueous ions. \Delta_{\text{hyd}}\text{H}^{\varnothing} is always exothermic since bonds are made between the ions and the water molecules.
\Delta_{\text{hyd}}\text{H}^{\varnothing} is larger when the charge density of the ion is higher since the ion will more strongly attract the water molecules. For example, fluoride ions will have more negative hydration enthalpies than chloride ions.
\text{X}_{\text{(g)}}\rarr\text{X}_{{(aq)}}
Enthalpy of Solution
The enthalpy of solution \left(\Delta_{\text{solution}}\text{H}^{\varnothing}\right), is the standard enthalpy change when one mole of an ionic solid completely dissolves in a solvent so that the ions are well separated and they do not interact with each other.
\Delta_{\text{solution}}\text{H}^{\varnothing} tends to be either mildly exothermic or endothermic.
If the \Delta_{\text{solution}}\text{H}^{\varnothing} solution is exothermic, the substance is most likely soluble. If the\Delta_{\text{solution}}\text{H}^{\varnothing} is endothermic, the substance is most likely insoluble.
\text{XY}_{\text{(s)}}\rarr\text{X}^+_{{(aq)}}+\text{Y}^-_{\text{(aq)}}
Lattice Enthalpy
Enthalpy of Lattice Formation \left(\Delta_{\text{latt}}\text{H}^{\varnothing}\right):
The enthalpy of lattice formation is the standard enthalpy change when one mole of an ionic crystal lattice is formed from its constituent ions in gaseous form. (\Delta_{\text{latt}}\text{H}^{\varnothing}) is usually negative (exothermic).
\text{X}^+_{\text{(g)}}+\text{Y}^-_{\text{(g)}}\rarr\text{XY}_{\text{(s)}}
It is possible to define the enthalpy of lattice dissociation. This is simply the negative equivalent of \left(\Delta_{\text{latt}}\text{H}^{\varnothing}\right).
Constructing Born-Haber Cycles
We construct Born-Haber cycles to calculate lattice enthalpy when it cannot be calculated directly. Using available data, we can create an enthalpy cycle that links all the different chemical processes together. The goal in the Born-Haber cycle is to us a series of enthalpic processes that will take us from a solid ionic lattice to sperate, non-interacting gaseous ions.
We start with a Born-Haber diagram containing only the process of lattice formation.
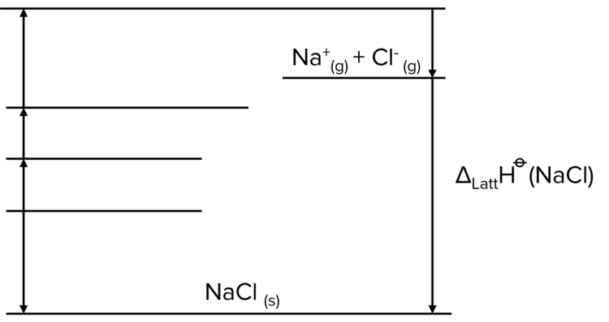
Our first task is to go from a solid ionic lattice to two separate elements. To do this use the reverse of the enthalpy of formation. Note that this is not the same as the lattice formation. Here we are moving from a solid lattice to elements in their standard states.
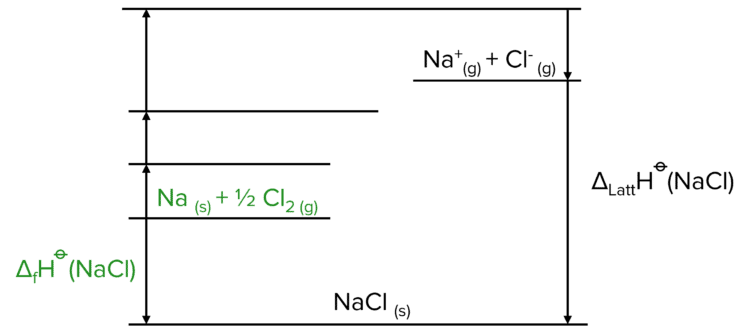
Now we need to create the cation (the positive ion in the lattice, usually the metal). This is done in two steps, first the atomisation of the metal element, and then the ionisation.
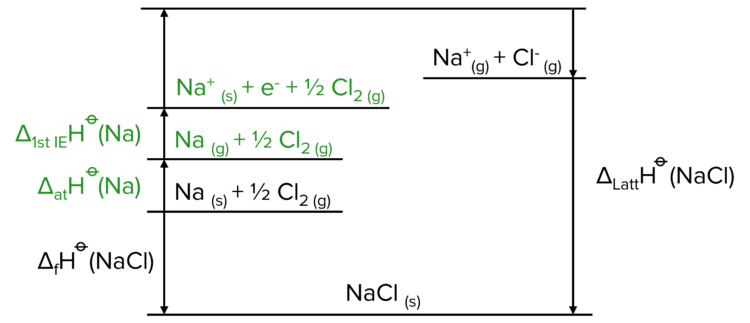
Finally, we need to create the anion (the negative ion in the lattice, usually the non-metal ion). To do this we follow a similar process to the one used above, but instead of ionisation, we use electron affinity.
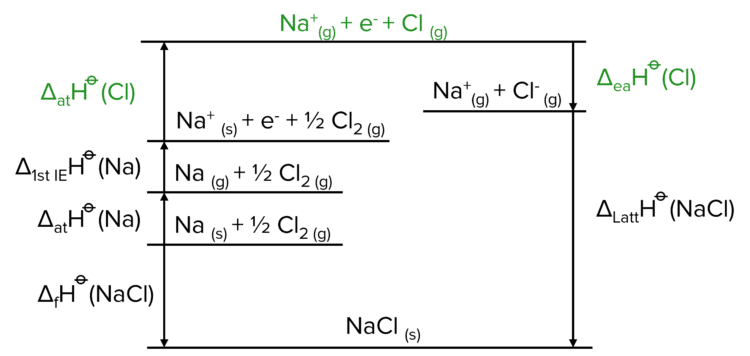
Once the cycle has been constructed, we can calculate the value of \Delta_{\text{latt}}\text{H}^{\varnothing} by following the alternate route provided. We again apply the convention that when moving with an arrow, we add the value the enthalpy and when moving against we subtract. This gives us:
\Delta_{\text{latt}}\text{H}^{\varnothing}=-\Delta_{\text{f}}\text{H}^{\varnothing}+\Delta_{\text{at}}\text{H}^{\varnothing}+\Delta_{\text{ie 1}}\text{H}^{\varnothing}+\Delta_{\text{at}}\text{H}^{\varnothing}+\Delta_{\text{ea 1}}\text{H}^{\varnothing}
Trends in Lattice Enthalpies
Lattice enthalpies become less negative as you go down a group due to the sizes of the ion. For example, \text{KCl} would be less negative than \text{LiCl}. The value of enthalpy of lattice formation depends on two main factors.
Charges of the Ions. The attraction between ions will be greater when the charges of the ions are bigger. This leads to a more negative value of enthalpy of lattice formation.
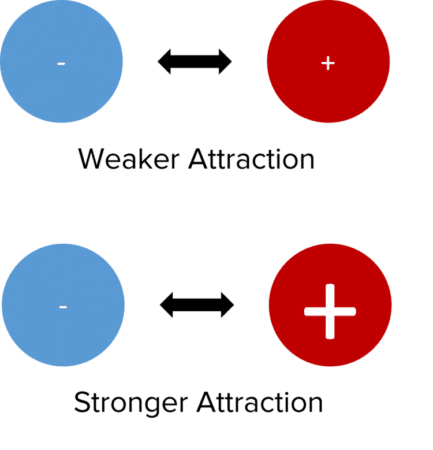
Sizes of the Ions. In lattices containing ions of significantly different sizes, the attractive forces between ions are weaker. This is because the ions are not as able to get as close together. This leads to a less negative value of the lattice enthalpy
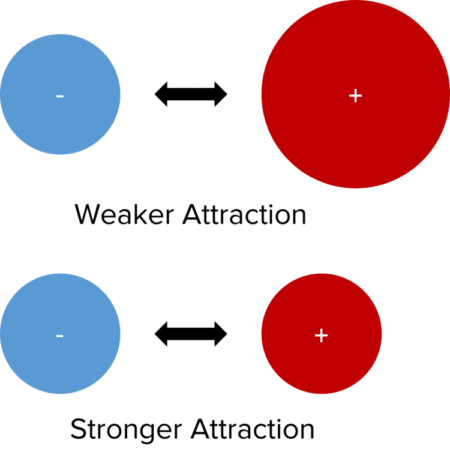
The Perfect Ionic Model
In the perfect ionic model, all ions in a lattice are 100\% ionic, perfectly spherical and only have electrostatic forces of attraction.
In reality, ionic substances can display covalent character. This means that the charge cloud isn’t perfectly spherical but is actually distorted. Ionic substances are more likely to have covalent character if there is a large difference in the size of the ions or there is a large difference in the charge of the ions

Theoretical lattice enthalpies assume that the perfect ionic model applies, so covalent character is not taken into account. Due to this assumption, for compounds that display covalent character, there can be differences between theoretical values and experimental (Born-Haber) values. The more covalent character displayed by a compound, the bigger the difference in values will be. Usually, Born-Haber values are larger than theoretical values since compounds with covalent character tend to have stronger lattices.
Example: Enthalpies of Solution
Calculate the enthalpy of hydration, in \text{kJ mol}^{-1}, of bromide ions given that the enthalpy of lattice formation of calcium bromide is \textcolor{#00bfa8}{-2170\text{kJ mol}}^{-1}, the enthalpy of solution of calcium bromide is \textcolor{#f21cc2}{-105\text{kJ mol}^{-1}} and the enthalpy of hydration of calcium ions is \textcolor{#a233ff}{-1661\text{kJ mol}^{-1}}.
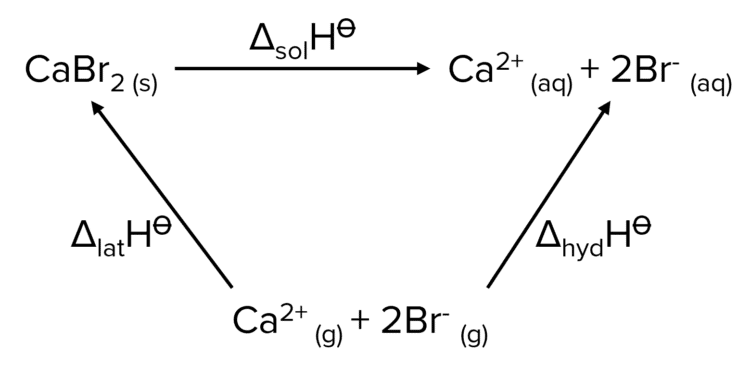
\Delta_{\text{solution}}\text{H}^{\varnothing}=\Delta_{\text{latt}}\text{H}^{\varnothing}+\Sigma\Delta_{\text{hyd}}\text{H}^{\varnothing}
[5 marks]
We must make sure that we take into account the fact that the formula for calcium bromide is \text{CaBr}_2 so the enthalpy of hydration of bromide is multiplied by 2. We also account for the fact that we are moving against the arrow of the formation enthalpy so we place a negative sign in front of its value.
\begin{aligned}\textcolor{#f21cc2}{-105} &= - (\textcolor{#00bfa8}{-2170}) + (\textcolor{#a233ff}{-1661} + 2x)\\\textcolor{#f21cc2}{-105} &= \textcolor{#00bfa8}{2170} - \textcolor{#a233ff}{1661} + 2x\\2x &= - \textcolor{#00bfa8}{2170} + \textcolor{#a233ff}{1661} - \textcolor{#f21cc2}{105}\\2x &= -614\\x &= \textcolor{#008d65}{-307\text{ kJ mol}^{-1}}\end{aligned}
Born - Haber Cycles Example Questions
Question 1: Explain the meaning of the term electron affinity.
[2 marks]
Enthalpy change when one mole of gaseous atoms form one mole of gaseous negative ions with a single charge.
Question 2: Define the term lattice enthalpy of dissociation.
[2 marks]
Enthalpy change when one mole of an ionic substance is separated into its constituent ions to form ions in the gaseous states.
Question 3: Fill in the Born-Haber cycle with the correct information. Label X, Y and the missing enthalpy changes.
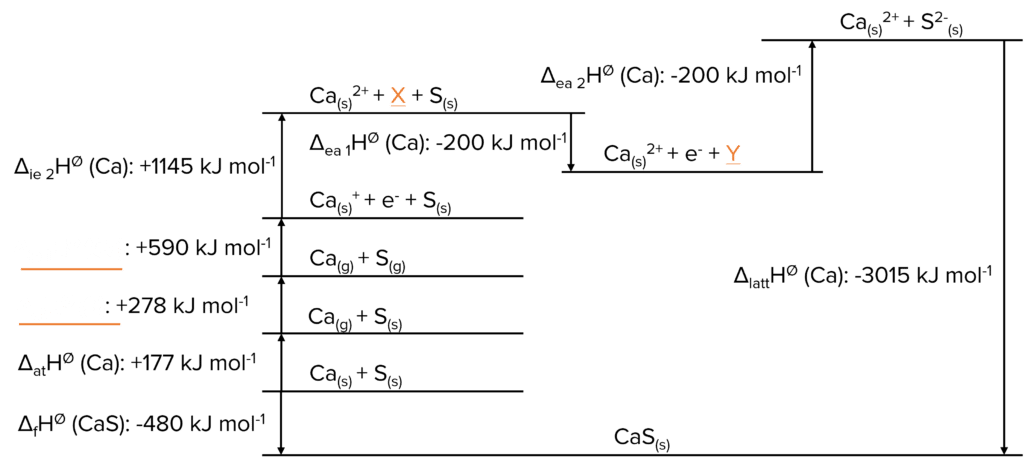
[4 marks]
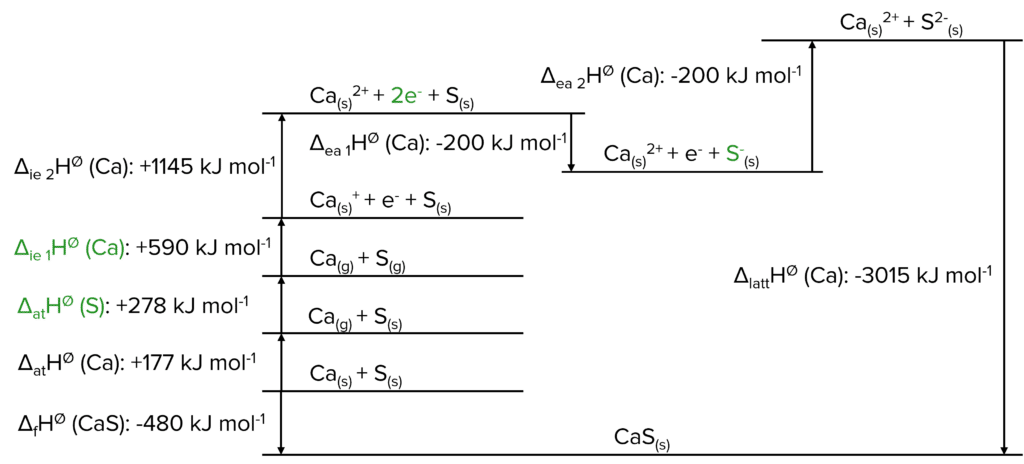
Question 4: Using the Born-Haber cycle given in Question 3, calculate \Delta_{\text{ea}}\text{H}^{\varnothing}\text{(S)}.
[2 marks]
Question 5: Explain the meaning of the term perfect ionic model.
Suggest two properties of ions that can influence the value of a lattice enthalpy calculated using a perfect ionic model.
No covalent character OR only electrostatic attraction OR ions are perfect spheres OR only ionic bonding
Any two from:
- Radius
- Size
- Distance between ions
- Ionic charge
- Charge density
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.