Hess Cycles and Bond Enthalpies
Hess Cycles and Bond Enthalpies Revision
Hess Cycles and Bond Enthalpies
Hess’s law is a version of the first law of thermodynamics that states that the total enthalpy change for a reaction is independent of the route the reaction takes.
The mean bond enthalpy is the enthalpy change that is needed to break the covalent bond in gaseous molecules, averaged over a range of measurements.
Hess’s Cycles
For many chemical processes, it is not possible to directly measure the enthalpy change. This can be for a variety of reasons, usually to do with the practicality or even feasibility of carrying out the experiment in a laboratory setting. In these cases, thermodynamics offers a clever work around. By using the enthalpy changes of other processes, we can construct an alternate pathway from reactants to products. It is possible to do this thanks to a principle known as Hess’s Law:
The total enthalpy change of a process is independent of the route taken.
This means that, by calculating the enthalpy changes of a set of alternate processes, we can calculate the overall enthalpy change of the reaction. To do this we construct what is know as a Hess cycle.
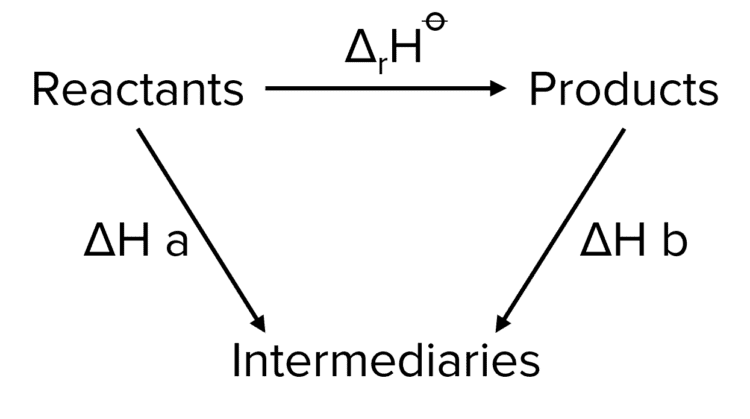
In the above reaction, the reaction can take two routes.
Route 1: \Delta_{\text{r}}\text{H}^{\varnothing}
Route 2:\Delta\text{H a}-\Delta\text{H b}
In route two, we are subtracting the value of \Delta\text{H} \text{ b}. We know that we need to subtract \Delta\text{H}\text{ b} as we are moving against the corresponding arrow in the Hess cycle. It is a widely adhered to convention that when preforming Hess cycle calculations, the values of enthalpies are additive (i.e. we are adding them in our expression) when moving with their corresponding arrow. When moving against the corresponding arrow we subtract their value.
Therefore we can define a general expression:
\Delta_{\text{f}}\text{H}^{\varnothing}=\triangle\text{H a}\pm\triangle\text{H b}\cdots
Whether or not we add or subtract a given enthalpy will determined by the above conventions.
Enthalpy of Combustion and Chain Length
There are a few important points to know about the enthalpy of combustion of hydrocarbon chains.
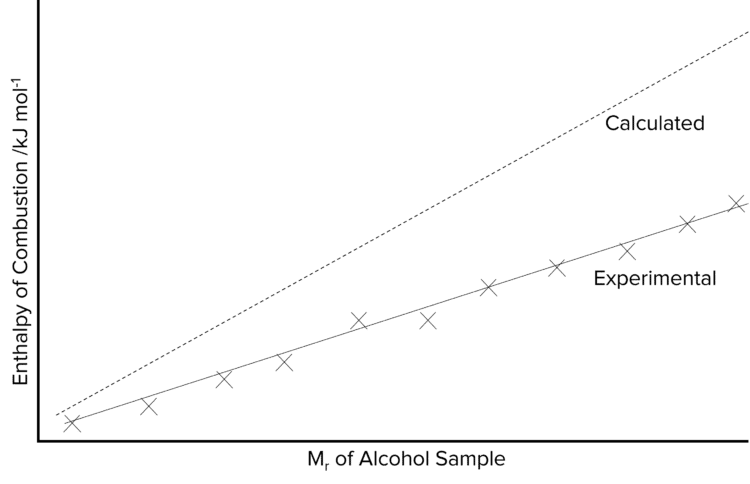
As the number of carbon atoms increases within a homologous series, such as alcohols or alkanes, the enthalpy of combustion increases. This is a result of the addition of new bonds. Bonds store energy and so increasing the number of bonds increases the amount of energy released when the chain is burnt. The enthalpy of combustion of hydrocarbon chains increases linearly with the length of the chain. This is because the value of the bond enthalpy for a carbon-carbon bond remains constant with each addition.
The values calculated from theory (e.g. by using Hess cycles) for the enthalpy of combustion for a carbon chain will typically be much higher than those determined from experiments. The discrepancy between the two will increase as chain length increases. This is a result of both heat loss during the experiment, as well as of incomplete combustion of the carbon chains. The likelihood of incomplete combustion will increase with chain length due higher the volumes of oxygen needed to completely burn longer chains. This accounts for the increase in the discrepancies between theoretical and experimental data.
Calculating Enthalpy Changes Using Enthalpy of Formation
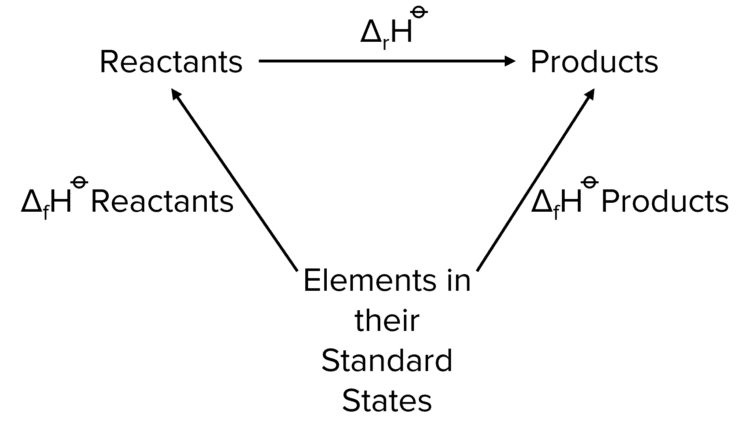
The standard enthalpy of formation is one of the more commonly known enthalpy values for a given substance. As such, it is common to use these values to calculate the overall enthalpy change of a reaction. The following equation is used:
\Delta\text{H}= \Sigma\Delta_{\text{f}}\text{H products}-\Sigma\Delta_{\text{f}}\text{H reactants}
Example: The following reaction takes place.
\text{Fe}_2\text{O}_{3\left(\text{s}\right)}+3\text{Ca}_{\left(\text{s}\right)}\rightarrow2\text{Fe}_{\left(\text{s}\right)}+3\text{CaO}_{\left(\text{s}\right)}
Provided below are the standard enthalpies of formation of the reactants and products.
| \text{Fe}_2\text{O}_{3 (s)} | \text{Ca}_{ (s)} | \text{Fe}_{ (s)} | \text{CaO}_{ (s)} | |
| \Delta_{\text{f}}\text{H}^{\varnothing}\text{ /kJ mol}^{-1} | \textcolor{#00bfa8}{-822} | \textcolor{#f21cc2}{0} | \textcolor{#a233ff}{0} | \textcolor{#eb6517}{-630} |
Construct a Hess cycle for this reaction. Use the data provided to calculate the enthalpy change during the reaction.
[4 marks]
Step 1: Construct the Hess cycle .
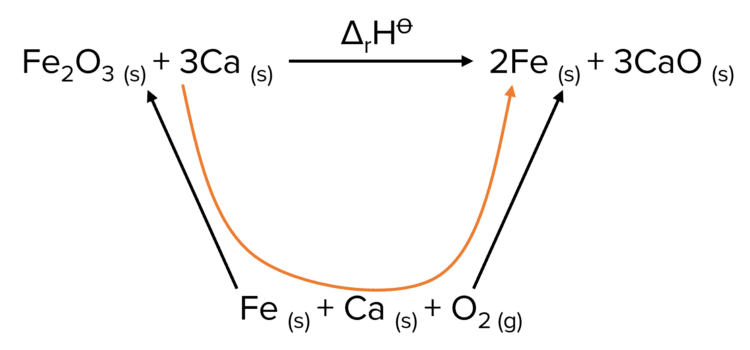
In this Hess cycle, the arrows come up from the reactants in their standard states to the reactants and the products. This represents the formation of the molecules from their constituent elements from their standard states.
Step 2: Calculate the enthalpy of reaction.
To calculate the enthalpy of the reaction we start at the reactants, then trace a path down through the constituent elements and back up to the products. To do this we move against the enthalpy of formation of the reactants and with the enthalpy of formation of the products.
This means that we are subtracting the enthalpy of formation of iron oxide and calcium and adding the enthalpy of formation of iron and calcium oxide.
\Delta_{\text{r}}\text{H}=[\textcolor{#a233ff}{0}+(3\times\textcolor{#eb6517}{-630})-[\textcolor{#f21cc2}{0}+(\textcolor{#00bfa8}{-882})]
Finally, as the enthalpies of formation for solid iron and calcium are 0 by default, we can ignore them in our calculation.
\begin{aligned}\Delta_{\text{r}}\text{H}&=(3\times\textcolor{#eb6517}{-630})-(\textcolor{#00bfa8}{-822})\\ &=-1890+822\\ &=\textcolor{#008d65}{-1068\text{ kJ mol}^{-1}}\end{aligned}
Calculating Enthalpy Changes Using Enthalpy of Combustion
Much like Enthalpies of Formation, it is possible to use standard enthalpies of combustion to construct an alternate path way to calculate reaction enthalpies. In the following example, standard enthalpies of combustion are used to calculate the value of \Delta_{\text{f}}\text{H} of ethanol by the following reaction.
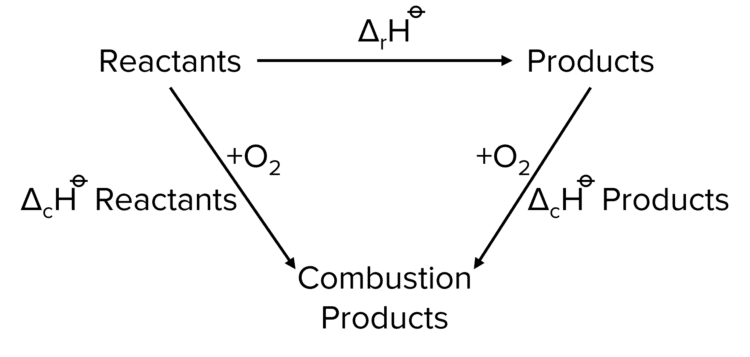
\Delta\text{H}=\Sigma\Delta_{\text{c}}\text{H reactants}-\Delta_{\text{c}}\text{H products}
2\text{C}_{\left(\text{s}\right)}+3\text{H}_{2\left(\text{g}\right)}+1.5\text{O}_{2\left(\text{g}\right)}\rightarrow\text{C}_2\text{H}_5\text{OH}_{\left(\text{l}\right)}
| \text{C}_{ (s)} | \text{H}_{2 (g)} | \text{C}_2\text{H}_5\text{OH}_{ (l)} | |
| \Delta_{\text{c}}\text{H}^{\varnothing}\text{ /kJ mol}^{-1} | \textcolor{#00bfa8}{-394} | \textcolor{#f21cc2}{-285} | \textcolor{#a233ff}{-1367} |
Note that no value is provided for the standard enthalpy of combustion of oxygen. This is because by definition the enthalpy of combustion of oxygen is 0.
Construct a Hess cycle for the reaction. Using the data above calculate the enthalpy of formation of ethanol.
[4 marks]
Step 1: Construct a Hess cycle.
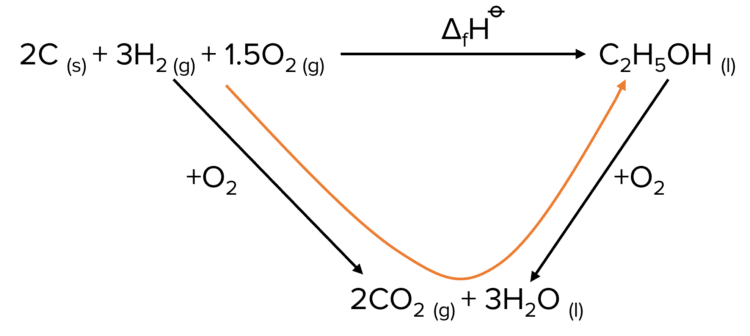
Step 2: Calculate the enthalpy of formation.
By following the path of the Hess cycle through the combustion products we move with the arrow of the combustion of the reactants and against that of the combustion of the products. This means that we are adding the enthalpy of combustion of reactants and subtracting the enthalpy of combustion of the products.
\begin{aligned}\Delta\text{H}&=[\left(2\times\textcolor{#00bfa8}{-394}\right)+\left(3\times\textcolor{#f21cc2}{(-285)}\right)]-\left(\textcolor{#a233ff}{-1367}\right)\\&=\left(-788+\left(-855\right)\right)-\left(-1367\right)\\&=-1643+1367\\&=\textcolor{#008d65}{-276 \text{ kJ mol}^{-1}}\end{aligned}
Calculating Bond Enthalpies
It is also possible to calculate enthalpies of reaction using bond energies. Here we consider the enthalpy of a reaction in terms of energy change involved in making and breaking chemical bonds. The first thing that has to happen in a reaction is that some bonds must broken. This will require the absorption of energy. The breaking of chemical bonds will make way for the formation of new ones, a process which releases energy. These two processes can then be taken together to give an overall enthalpy change in the reaction:
\Delta\text{H}=\Sigma\text{ bond energies broken}-\Sigma\text{ bond energies made}
The substances involved in these calculations must all be in a gaseous state.
Example: Calculate the enthalpy of formation of \text{NH}_3 using the mean bond energy data.
[4 marks]
0.5\text{N}_2+1.5\text{H}\rightarrow2\text{NH}_3
| Bond | Mean Bond Energy /\text{kJ mol}^{-1} |
| \text{N}\equiv\text{N} | \textcolor{#00bfa8}{941} |
| \text{H}-\text{H} | \textcolor{#f21cc2}{436} |
| \text{N}-\text{H} | \textcolor{#a233ff}{391} |
Step 1: Count the number of bonds broken and made.
| Bond | Number Broken | Number Made |
| \text{N}\equiv\text{N} | 0.5 | 0 |
| \text{H}-\text{H} | 1.5 | 0 |
| \text{N}-\text{H} | 0 | 3 |
Step 2: Calculate the enthalpy of the reaction:
\begin{aligned}\Delta\text{H}&=[(0.5\times\textcolor{#00bfa8}{941})+(1.5\times\textcolor{#f21cc2}{436})]-[3\times\textcolor{#a233ff}{391}]\\ &=1124.5-1173\\ &=\textcolor{#008d65}{-48.5\text{ kJ mol}^{-1}}\end{aligned}
Note: \Delta\text{H} that is calculated using bond energies data is less accurate than using formation or combustion data since mean bond energies are an average and not exact.
Hess Cycles and Bond Enthalpies Example Questions
Question 1: Use the standard enthalpies of formation in the table and the equation to calculate the standard enthalpy of change for this reaction.
| \text{Sb}_2\text{O}_{3 (s)} | \text{CO}_{ (g)} | \text{Sb}_{ (l)} | \text{CO}_{2 (g)} | |
| \Delta_{\text{f}}\text{H}^{\varnothing}\text{ /kJ mol}^{-1} | -704 | -110 | +21 | -395 |
\text{Sb}_2\text{O}_{3\left(\text{s}\right)}+3\text{CO}_{\left(\text{g}\right)}\rightarrow2\text{Sb}_{\left(\text{l}\right)}+3\text{CO}_{2\left(\text{g}\right)}
[3 marks]
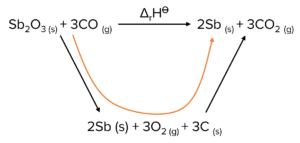
\Delta_{\text{f}}=\Sigma\triangle\text{H}_{\text{f}}\text{H products}-\Sigma\Delta_{\text{f}}\text{H reactants}
\Delta\text{H}_{\text{f}}=\left(\left(2\times21\right)+\left(3\times-395\right)\right)-\left(-704+\left(3\times-110\right)\right)=\left(-1143-\left(-1034\right)\right)=-109\text{kJ mol}^{-1}
Question 2: Use the standard enthalpies of combustion in the table and the equation to calculate the standard enthalpy of change for this reaction.
| \text{C}_{(s)} | \text{H}_2 | \text{C}_7\text{H}_{8 (l)} | |
| \Delta_{\text{c}}\text{H}^{\varnothing}\text{ /kJ mol}^{-1} | -394 | -287 | -3909 |
7\text{C}_{\left(\text{s}\right)}+4\text{H}_{2\left(\text{g}\right)}\rightarrow\text{C}_7\text{H}_{8\left(\text{l}\right)}
[3 marks]
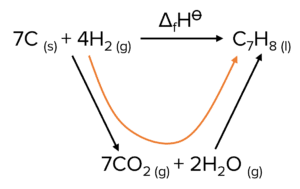
\Delta\text{H}=\Sigma\Delta_{\text{c}}\text{H reactants}-\Sigma\Delta_{\text{c}}\text{H products}
\Delta\text{H}=\left(\left(7\times-393\right)+\left(4\times-287\right)\right)-\left(-3909\right)=-3899+3909
=+10\text{ kJ mol}^{-1}
Question 3: Methane reacts with fluorine in the following equation.
\text{CH}_{4\left(\text{g}\right)}+4\text{F}_{2\left(\text{g}\right)}\rightarrow\text{CF}_{4\left(\text{l}\right)}+4\text{HF}_{\left(\text{g}\right)}
\Delta\text{H}=-1904\text{ kJ mol}^{-1}
| \text{C}-\text{H} | \text{C}-\text{F} | \text{H}-\text{F} | |
| Mean Bond Enthalpy/\text{ kJ mol}^{-1} | 410 | 486 | 562 |
A student suggested that the F-F bond is quite weak. Using the data and calculations, is the student correct?
[4 marks]
\Delta\text{H}=\Sigma\text{bond energies broken}-\Sigma\text{bond energies made}
Bonds broken: \left(4\times410\right)+\left(4\times\text{F-F}\right)
Bonds formed: \left(4\times386\right)+\left(4\times562\right)
-1904=\left(\left(4\times410\right)+\left(4\times\text{F-F}\right)\right)-\left(\left(4\times386\right)+\left(4\times562\right)\right)
4\text{F-F}=-1904-\left(4\times410\right)+\left(\left(4\times486\right)+4\times562\right)=648
\text{F-F}=648\div4=162\text{ kJ mol}^{-1}
The student is correct because the F-F bond energy is less than other covalent bonds.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.