The Modulus Function
The Modulus Function Revision
The Modulus Function
The modulus of a number is the size of the number, whether it is negative or positive, for example the modulus of 6 is 6 and the modulus of -6 is 6.
Modulus Notation
The following notation is relevant to the modulus:
- The modulus of a number, e.g. x is written as |x|.
- Generally, |x| = x for x \geq 0, and |x| = -x for x <0
- Functions also have a modulus: e.g. if f(x) = -2, then |f(x)| = 2
- |f(x)| = f(x) when f(x) \geq 0 and |f(x)| = -f(x) when f(x)<0
- If the modulus is inside the function, e.g. f(|x|), then you apply the modulus to the x-value before applying the function, i.e. f(|-4|) = f(4)
Graphs of Modulus Functions – Straight Lines
There are 3 types of modulus graphs that you may be asked to draw:
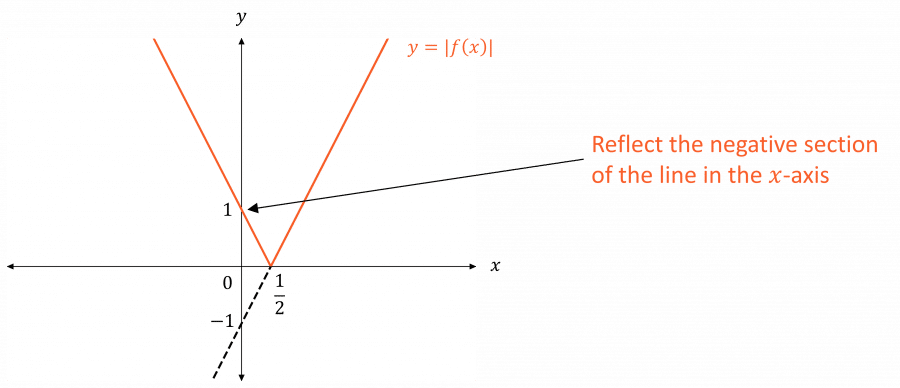
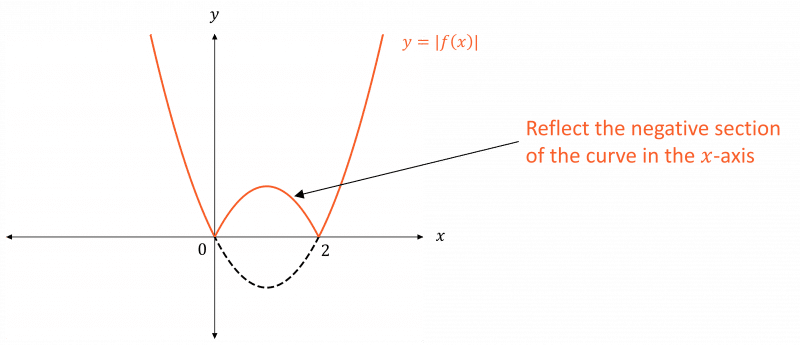
- y = |f(x)| – all negative values of f(x) are made positive, by reflecting the negative section of the graph of f(x) in the x-axis. This restricts the range to |f(x)| \geq 0 (or a subset within |f(x)| \geq 0, e.g. |f(x)| \geq 2.
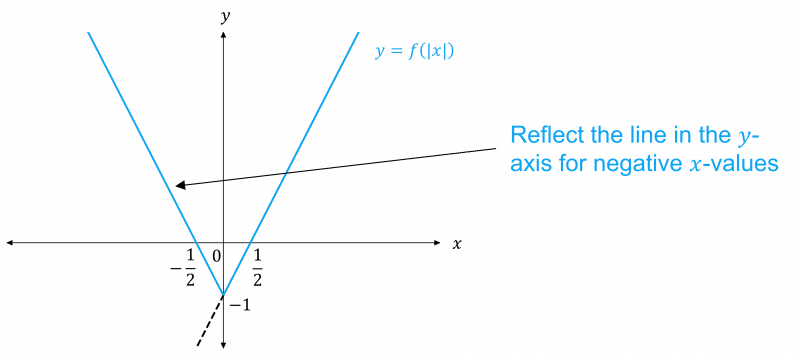
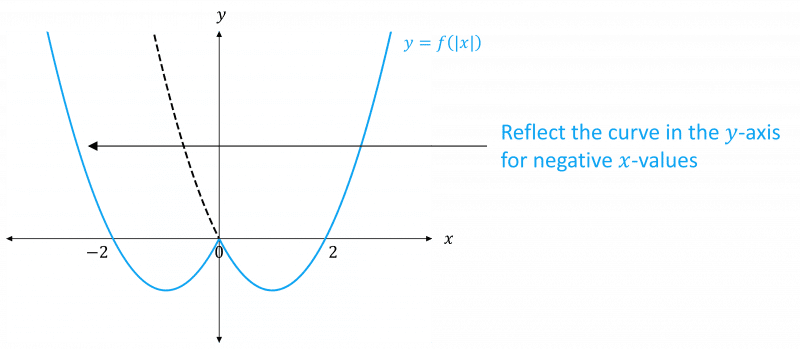
- y = f(|x|) – the negative x-values give the same result as the corresponding positive x-values, so the graph of f(x) for x \geq 0 is reflected in the y-axis, for negative x-values.
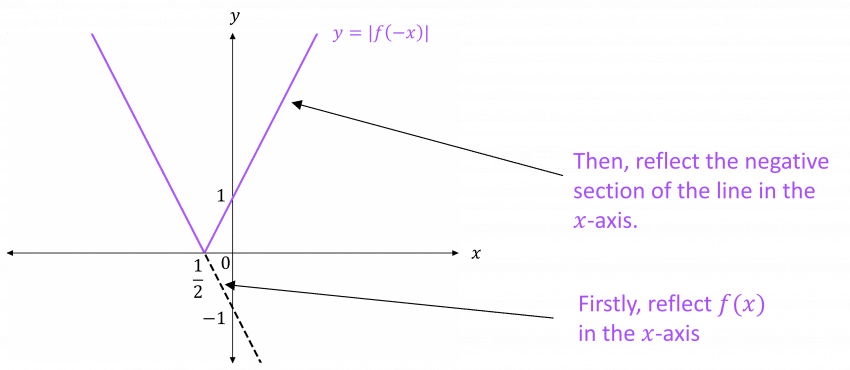
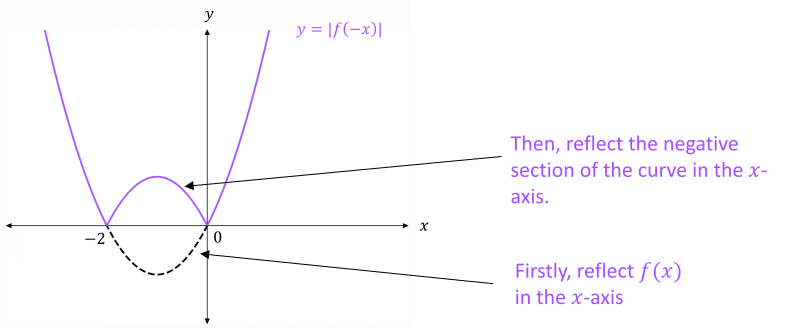
- y = |f(-x)| – the x-values swap sign (i.e. from positive to negative of from negative to positive), so the graph of f(x) is reflected in the y-axis. Then, all negative values of f(x) are made positive by reflecting the negative section of the graph of f(x) in the x-axis. The range is restricted, as with y = |f(x)|.
The best and easiest way to draw these graphs is to plot the graph of y = f(x) first, and then reflect it in the appropriate axis or axes.
Example: For f(x) = 2x-1, sketch the graphs of
\begin{aligned} y &= |f(x)| \\ y &= f(|x|) \\ y &= f|(-x)| \end{aligned}
Graphs of Modulus Functions – Quadratics and Cubics etc.
For modulus graphs where the function is a quadratic or cubic etc. the same rules apply as for straight lines – however, sketching them will be a little bit harder.
Example: For f(x) = x^2-2x, sketch the graphs of
\begin{aligned} y &= |f(x)| \\ y &= f(|x|) \\ y &= |f(-x)| \end{aligned}
Solving Modulus Equations Graphically
To solve modulus equations of the form |f(x)| = n or |f(x)| = |g(x)|, you can solve them graphically, using the following method:
Step 1: Sketch the graphs of y = |f(x)| and y = n, on the same pair of axes.
Step 2: Work out the ranges of x for which f(x) \geq 0 and f(x) < 0 from the graph.
e.g. f(x) \geq 0 for x \leq \textcolor{red}{a} or x \geq \textcolor{blue}{b} and f(x) < 0 for \textcolor{red}{a} < x < \textcolor{blue}{b}
Step 3: Use step 2 to write 2 new equations, one that holds for each range of x:
f(x) = n for x \leq \textcolor{red}{a} or x \geq \textcolor{blue}{b}
- f(x) = n for \textcolor{red}{a} < x < \textcolor{blue}{b}
Step 4: Solve each equation in turn and check that the solutions are valid, and remove any that are outside the range of x for that equation.
Step 5: Check that the solutions look correct, by looking at the graph.
Note: Use the same method for |f(x)| = |g(x)|, by replacing n with g(x).
Solving Modulus Equations Algebraically
For equations of the form |f(x)| = n and |f(x)| = g(x) you can solve them algebraically instead of graphically – if you feel that you understand the topic well enough.
Example: Solve |2x+2| = x+4
Step 1: Solve for positive values:
\begin{aligned} 2x + 2 &= x+4 \\ \textcolor{red}{x} &= \textcolor{red}{2} \end{aligned}
Step 2: Solve for negative values:
\begin{aligned} -(2x + 2) &= x+4 \\ 3x &= -6 \\ \textcolor{red}{x} &= \textcolor{red}{-2} \end{aligned}
Step 3: Combine the solutions:
The solutions are \textcolor{red}{x = 2} and \textcolor{red}{x = -2}
For equations of the form |f(x)| = |g(x)|, it is easier to do solve them algebraically, using the following rule:
“If |a| = |b|, then a^2 = b^2 ”
So if |f(x)| = |g(x)|, then [f(x)]^2 = [g(x)]^2
Example: Solve |x-1| = |2x+3|
Step 1: Square both sides:
\begin{aligned} |x-1| &= |2x+3| \\ (x-1)^2 &= (2x+3)^2 \end{aligned}
Step 2: Expand and simplify:
\begin{aligned} x^2 - 2x + 1 &= 4x^2 + 12x + 9 \\ 3x^2 + 14x + 8 &= 0 \\ (3x+2)(x+4) &= 0 \end{aligned}
Step 3: So, the solutions are:
\textcolor{red}{x = - \dfrac{2}{3}} and \textcolor{red}{x = -4}
Note:
You can also solve modulus inequalities using these methods. The graphical method of solving inequalities will be helpful, since there will often be a quadratic involved. Another rule that will be helpful is:
|x-a| < b \, \iff \, a - b < x < a+b
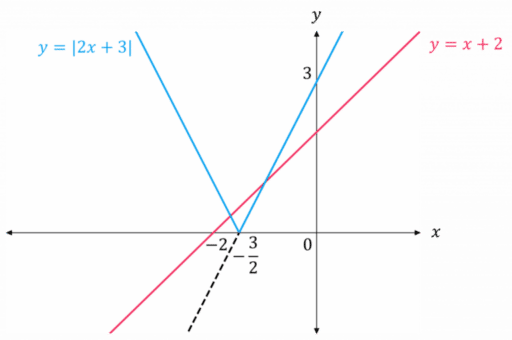
Example 1: Solving Modulus Equations Graphically – Straight Lines
Solve |2x+3| = x+2
[3 marks]
Step 1: Sketch the graphs of y = |2x+3| and y = x+2 on the same pair of axes.
Step 2: Work out the ranges of x for which f(x) \geq 0 and f(x) < 0 from the graph:
2x+3 \geq 0 for x \geq - \dfrac{3}{2} and 2x+3 < 0 for x < - \dfrac{3}{2}
Step 3: Use step 2 to write 2 new equations, one that holds for each range of x:
(1) 2x+3 = x+2 for x \geq - \dfrac{3}{2}
(2) - (2x+3) = x+2 for x < - \dfrac{3}{2}
Step 4: Solve each equation in turn and check that the solution are valid, and remove any that are outside the range of x for that equation.
Solving (1): x=-1 (this is valid since -1 \geq - \dfrac{3}{2})
Solving (2): 3x = -5 \Rightarrow x = - \dfrac{5}{3} (this is valid since - \dfrac{5}{3} < - \dfrac{3}{2})
Step 5: Check that the solutions look correct, by looking at the graph. The two solutions appear to be correct.
Example 2: Solving Modulus Equations Graphically – Quadratics and Cubics etc.
Solve |x^2 - 4| = 3
[4 marks]
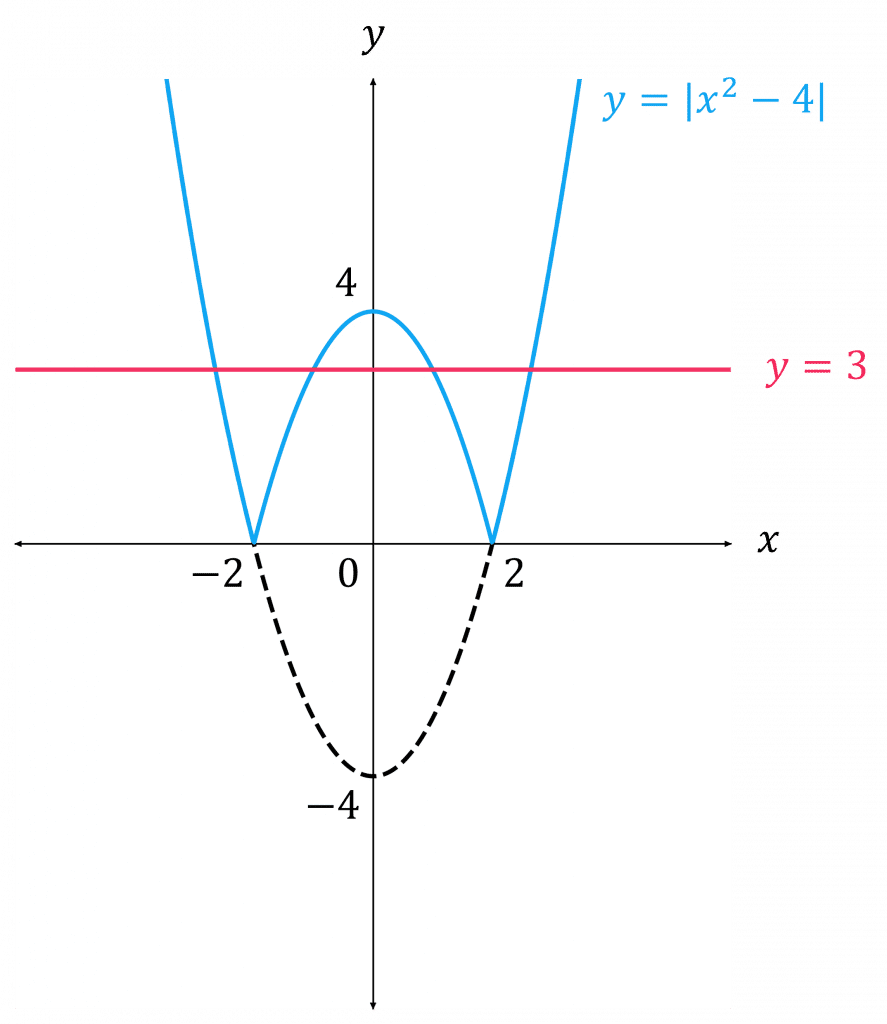

Step 1: Sketch the graphs of y = |x^2-4| and y = 3 on the same pair of axes.
Step 2: Work out the ranges of x for which f(x) \geq 0 and f(x) < 0 from the graph:
x^2 - 4 \geq 0 for x \leq -2 or x \geq 2
and x^2 - 4 < 0 for -2 < x < 2
Step 3: Use step 2 to write 2 new equations, one that holds for each range of x:
(1) x^2 - 4 = 3 for x \leq -2 or x \geq 2
(2) - (x^2 - 4) = 3 for -2 < x < 2
Step 4: Solve each equation in turn and check that the solution are valid, and remove any that are outside the range of x for that equation.
Solving (1): x^2 = 7 \Rightarrow x = \sqrt{7} and x = - \sqrt{7} (this is valid since - \sqrt{7} \leq - 2 and \sqrt{7} \geq 2)
Solving (2): x^2 - 1 = 0 \Rightarrow x = 1 and x = -1 (this is valid since 1 and -1 both lie within -2 < x < 2)
Step 5: Check that the solutions look correct, by looking at the graph. The four solutions appear to be correct.
The Modulus Function Example Questions
Question 1: For the function f(x) = 3x^2 + 4x - 9, find the following:
a) f(-2)
b) |f(-2)|
c) f(|-2|)
d) -|f(2)|
[4 marks]
a) f(-2) = 3(-2)^2 + 4(-2) - 9 = -5
b) |f(-2)| = |-5| = 5
c) f(|-2|) = f(2) = 3(2)^2 + 4(2) - 9 = 11
d) - |f(2)| = - |11| = - 11
Question 2:
a) For the function f(x) = 3x-3, x \in \mathbb{R}, sketch the graphs of:
i) y = |f(x)|
ii) y = f(|x|)
iii) y = |f(-x)|
b) Hence, or otherwise, solve the equation |3x - 3| = \dfrac{3}{2}
[7 marks]
a)i) The negative section needs to be reflected in the x-axis:
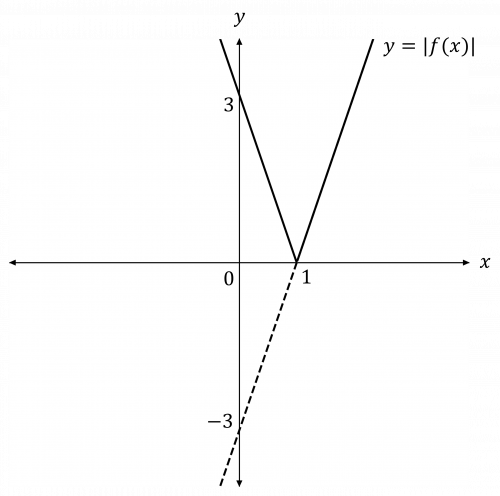
ii) For the negative x-values, reflect the line in the y-axis:

iii) Reflect f(x) in the y-axis, and then reflect the negative section in the x-axis:
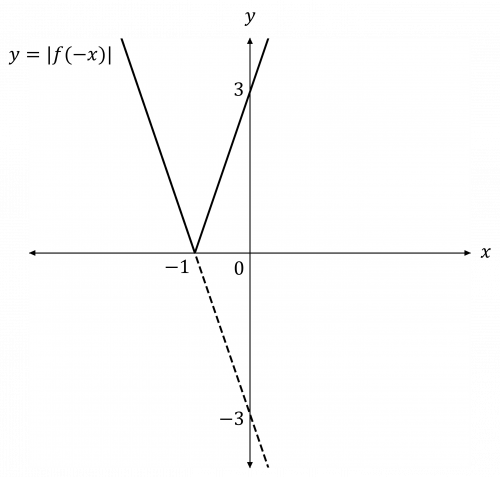
b)
Firstly, sketch the graphs of y = |3x - 3| (using part a)i)) and y = \dfrac{3}{2} on the same pair of axes:
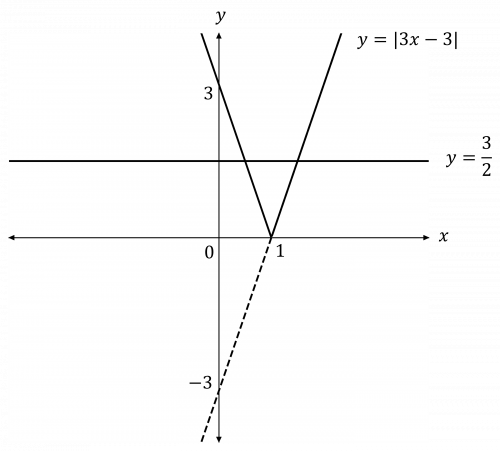
3x - 3 \geq 0 when x \geq 1 and 3x - 3 < 0 when x < 1
So, we can form two equations:
(1) 3x - 3 = \dfrac{3}{2} for x \geq 1
(2) -(3x-3) = \dfrac{3}{2} for x < 1
Then, we can solve these:
Solving (1): 3x = \dfrac{9}{2} \Rightarrow x = \dfrac{3}{2} for x \geq 1 (this is valid since \dfrac{3}{2} \geq 1)
Solving (2): 3x = \dfrac{3}{2} \Rightarrow x = \dfrac{1}{2} for x < 1 (this is valid since \dfrac{1}{2} < 1)
From looking at the graph, both solutions seem to be correct.
Question 3: Solve the equation 2|-x-3| = x+4
[3 marks]
Therefore 2(-x-3) = x+4 or -2(-x-3) = x+4
Then, solve these:
\begin{aligned} 2(-x-3) &= x + 4 \\ -2x - 6 &= x + 4 \\ 3x &= - 10 \\ x &= - \dfrac{10}{3} \end{aligned}
\begin{aligned}-2(-x-3) &= x + 4 \\ 2x + 6 &= x + 4 \\ x &= - 2 \end{aligned}
So, x = - \dfrac{10}{3} or x = - 2
Question 4: Solve the equation |2x+4| = -2|x+1|
[3 marks]
Actually, we need not do any calculation at all. On the left side of the equation, we have |2x + 4|, which is defined to be always positive.
However, the right side of the equation is always negative (as we have -2 multiplied by an always-positive term).
We can conclude, then, that there could only be a solution if both graphs meet at the x-axis.
However, this is not the case as the first graph touches the x-axis at x=-2 while the second graph touches the x-axis at x=-1.
Hence, there are no solutions.
Question 5: Solve the equation |2x+2| = |x-2|
[4 marks]
\begin{aligned} |2x+2| &= |x-2| \\ (2x+2)^2 &= (x-2)^2 \\ 4x^2 + 8x + 4 &= x^2 - 4x + 4 \\ 3x^2 + 12x &= 0 \\ x^2 + 4x &= 0 \\ x(x+4) &= 0 \end{aligned}
Hence, x = 0 or x = -4
The Modulus Function Worksheet and Example Questions
Functions
A LevelYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






