Newton-Raphson Method
Newton-Raphson Method Revision
Newton-Raphson Method
The Newton-Raphson Method is a different method to find approximate roots. The method requires you to differentiate the equation you’re trying to find a root of, so before revising this topic you may want to look back at differentiation to refresh your mind.
Using the Newton-Raphson Method
Finding roots of an equation in the form f(x)=0, requires you to find f'(x) and then use the following formula:
\Large{x_{n+1}=x_n-\dfrac{f(x_n)}{f'(x_n)}}
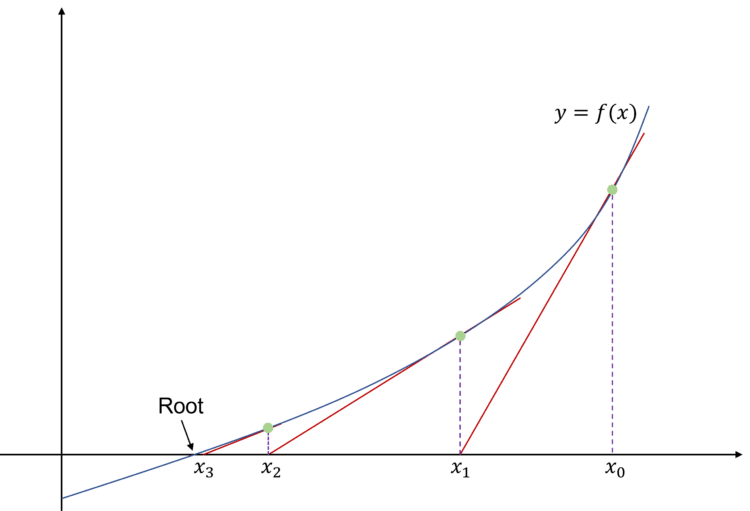
This method iteratively finds the x-intercept of the tangent to the graph of f(x) at x_n and then uses this value as x_{n+1}.
Why the Newton-Raphson Method Can Fail
- Similar to other iteration formulas, if your starting point of x_0 is too far away from the actual root, the Newton-Raphson method may diverge away from the root.
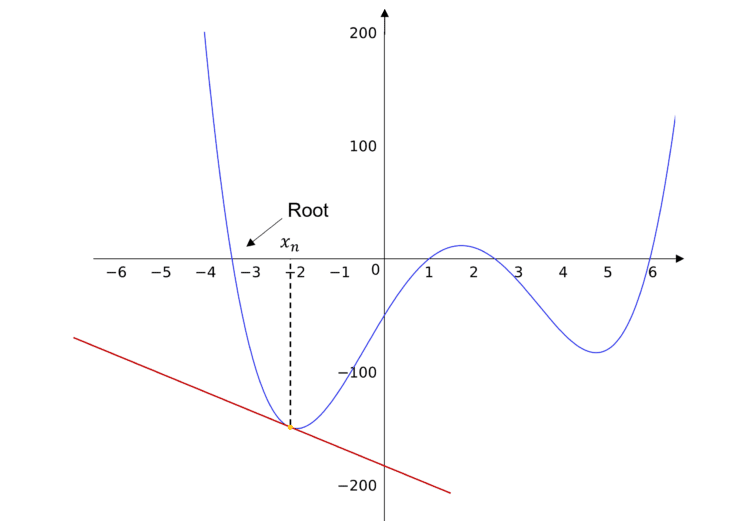
- The Newton-Raphson method can also fail if the gradient of the tangent at x_n is close or equal to \textcolor{red}{0}. This is shown in the diagram below, where the tangent has a gradient very close to 0, so the point where it meets the x-axis will be very far away from the root, so the sequence of iterations may diverge.
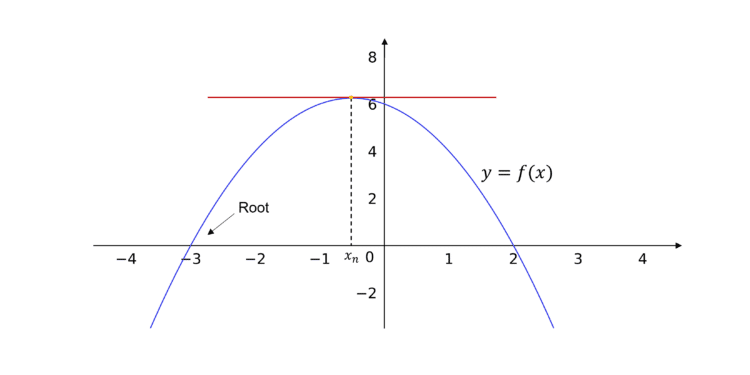
- Furthermore, if the tangent at a point on f(x) is horizontal, i.e. x_n is a stationary point, then the Newton-Raphson method will fail. This is because the tangent will never meet the x-axis, so there will be no further iterations. In addition to this, the tangent is horizontal when f'(x)=0, so the formula would not work as you cannot divide by 0.
A Level Maths Predicted Papers 2024
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A Level Maths Revision Cards
The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. MME is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
Example: The Newton Raphson Method
Find a root of the equation x^2-8x+11=0 to 5 decimal places using x_0=6
First we need to differentiate f(x)=x^2-8x+11:
f'(x)=2x-8Substituting this into the Newton-Raphson formula:
x_{n+1}=x_n-\dfrac{x^2-8x+11}{2x-8}Starting with x_0=6:
x_1=6-\dfrac{6^2-8(6)+11}{2(6)-8}=6.25Using the formula again to find the following iterations:
x_2=6.25-\dfrac{6.25^2-8(6.25)+11}{2(6.25)-8}=6.236111111x_3=6.236111111-\dfrac{6.236111111^2-8(6.236111111)+11}{2(6.236111111)-8}=6.236067978
x_4=6.236067978-\dfrac{6.236067978^2-8(6.236067978)+11}{2(6.236067978)-8}=6.236067977
Thus a root of x^2-8x+11=0 is 6.23607 to 5 decimal places.
Newton-Raphson Method Example Questions
Question 1: Use the Newton-Raphson method with x_0=1, to find a root of the equation x^3-2x^2-5x+8=0 to 5 decimal places.
[4 marks]
Firstly we need to differentiate f(x)=x^3-2x^2-5x+8
f'(x)=3x^2-4x-5
Now we need to apply the Newton-Raphson formula, starting with x_0=1:
x_1=1-\dfrac{1^3-2(1)^2-5(1)+8}{3(1)^2-4(1)-5}=\dfrac{4}{3}
x_2=\dfrac{4}{3}-\dfrac{(\dfrac{4}{3})^3-2(\dfrac{4}{3})^2-5(\dfrac{4}{3})+8}{3(\dfrac{4}{3})^2-4(\dfrac{4}{3})-5}=1.362962963
x_3=1.362962963-\dfrac{(1.362962963)^3-2(1.362962963)^2-5(1.362962963)+8}{3(1.362962963)^2-4(1.362962963)-5}=1.36332811
x_4=1.36332811-\dfrac{(1.36332811)^3-2(1.36332811)^2-5(1.36332811)+8}{3(1.36332811)^2-4(1.36332811)-5}=1.363328238
So a root of x^3-2x^2-5x+8=0 is 1.36333 to 5 decimal places.
Question 2: Use the Newton-Raphson method with x_0=2, to find a root of the equation 3x\ln{x}=7 to 4 significant figures.
[5 marks]
Firstly, we need to rearrange the equation so it is in the form f(x)=0:
3x\ln{x}-7=0
Then we need to differentiate f(x)=3x\ln{x}-7, to do this we will need to use the product rule:
\begin{aligned} f'(x) &=3\ln{x}+3x\times \dfrac{1}{x} \\ &=3\ln{x}+3 \\ &=3(\ln{x}+1) \end{aligned}
Now we need to apply the Newton-Raphson formula starting with x_0=2:
x_1=2-\dfrac{3(2)\ln{2}-7}{3(\ln{2}+1)}=2.559336473
x_2=2.559336473-\dfrac{3(2.559336473)\ln{2.559336473}-7}{3(\ln{2.559336473}+1)}=2.522322342
x_3=2.522322342-\dfrac{3(2.522322342)\ln{2.522322342}-7}{3(\ln{2.522322342}+1)}=2.522182638
x_4=2.522182638-\dfrac{3(2.522182638)\ln{2.522182638}-7}{3(\ln{2.522182638}+1)}=2.522182636
So the root of 3x\ln{x}=7 is 2.522 to 4 significant figures.
Question 3: Explain why starting with x_0=0.5 for the equation -x^2+x+12=0 will fail when using the Newton-Raphson method.
[2 marks]
Differentiating f(x)=-x^2+x+12:
f'(x)=-2x+1
Substituting in x=0.5:
f'(0)=-2(0.5)+1=0
Thus, the Newton-Raphson method will fail because you cannot divide by 0
Newton-Raphson Method Worksheet and Example Questions
Newton-Raphson Method and Other Recurrence Relations
A LevelYou May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
