Iterative Methods
Iterative Methods Revision
Iterative Methods
Using iteration allows you to find approximate roots to a given level of accuracy. When using iterative methods, you substitute an approximate value of the root into an iteration formula, and then you substitute this new approximate root back in until you get a root that is to the desired accuracy.
Forming Iteration Formulas by Rearranging Equations
Iteration formulas are formed by rearranging equations and isolating a single variable.
There are many ways to rearrange equations, and not all will give you an iteration formula that converges to give a root. So an exam question will most likely ask you to show that an equation can be rearranged into a specific form.
Example:
Show that 2x^3-3x-5=0 can be rearranged to: x=\sqrt[3]{\dfrac{3x+5}{2}}
First add 3x+5 to both sides to give:
2x^3=3x+5
Next divide both sides by 2:
x^3=\dfrac{3x+5}{2}
Finally take the cube root of both sides:
x=\sqrt[3]{\dfrac{3x+5}{2}}
Therefore, the iteration formula is: x_{n+1}=\sqrt[3]{\dfrac{3x_{n}+5}{2}} to find approximate roots.
Using Iterations to Draw Diagrams
After you have used an iteration method, you can form a sequence of iterations using x_{n+1}=f(x_n) and then plot these points on a diagram to show whether the sequence converges or diverges.
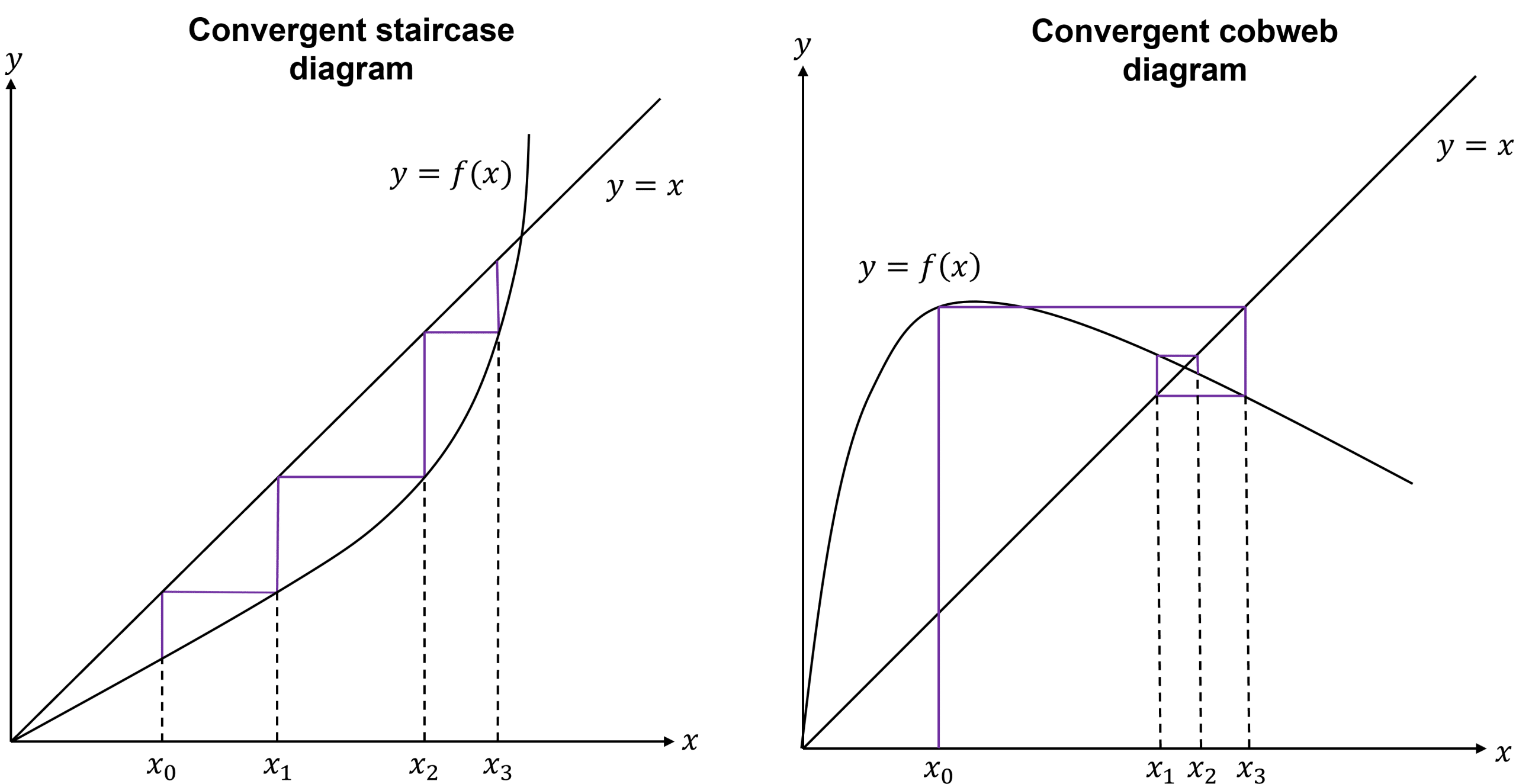
Forming iteration diagrams
1) Sketch the graphs of y=x and y=f(x), where f(x) is the iterative formula. The root of the original equation is the point of intersection of the two graphs.
2) From your starting point x_0 draw a vertical line until it meets y=x
3) Next draw a horizontal line from this point to the line y=f(x). This point is the first iteration, x_1.
4) After this, draw a vertical line from this point to the line y=x and then a horizontal line to y=f(x). Repeat this step for the remaining iterations.
5) If after each step points are getting closer to the roots, the sequence is converging. If after each step the points are getting further away from the root, the sequence is diverging.
There are two types of diagrams – staircase diagrams and cobweb diagrams.
In convergent staircase diagrams, the iterations increasingly get closer to the root.
In convergent cobweb diagrams, the iterations alternate between going above and below the root, progressively getting closer.
Example 1: Iteration Formula
Starting with x_0=1, use the iteration formula x_{n+1}=\sqrt{\dfrac{9}{x_{n}+1}} to solve x^3+x^2-9=0 to 1 decimal place.
x_n denotes the approximation of the solution at the nth iteration
Starting with x_0=1, x_1=\sqrt{\dfrac{9}{1+1}}=2.121320344
Substitute this value back into the iteration formula, x_2=\sqrt{\dfrac{9}{2.121320344+1}}=1.698056292
Repeat the previous step until you get consecutive answers that are the same when rounded to 1 decimal place.
So,
x_3=\sqrt{\dfrac{9}{1.698056292+1}}=1.826399382
Then,
x_4=\sqrt{\dfrac{9}{1.826399382+1}}=1.784450437
As we can see, x_3 and x_4 both round to the same value to 1 decimal place, so the root is x=1.8
Example 2: Drawing Iteration Diagrams
7x-x^2+12=0 can be rearranged to give the iteration formula: x_n=\sqrt{7x+12}
Starting with x_0=8, use the iteration formula to find x_1, x_2 and x_3 and hence sketch a diagram to show that the sequence x_n converges.
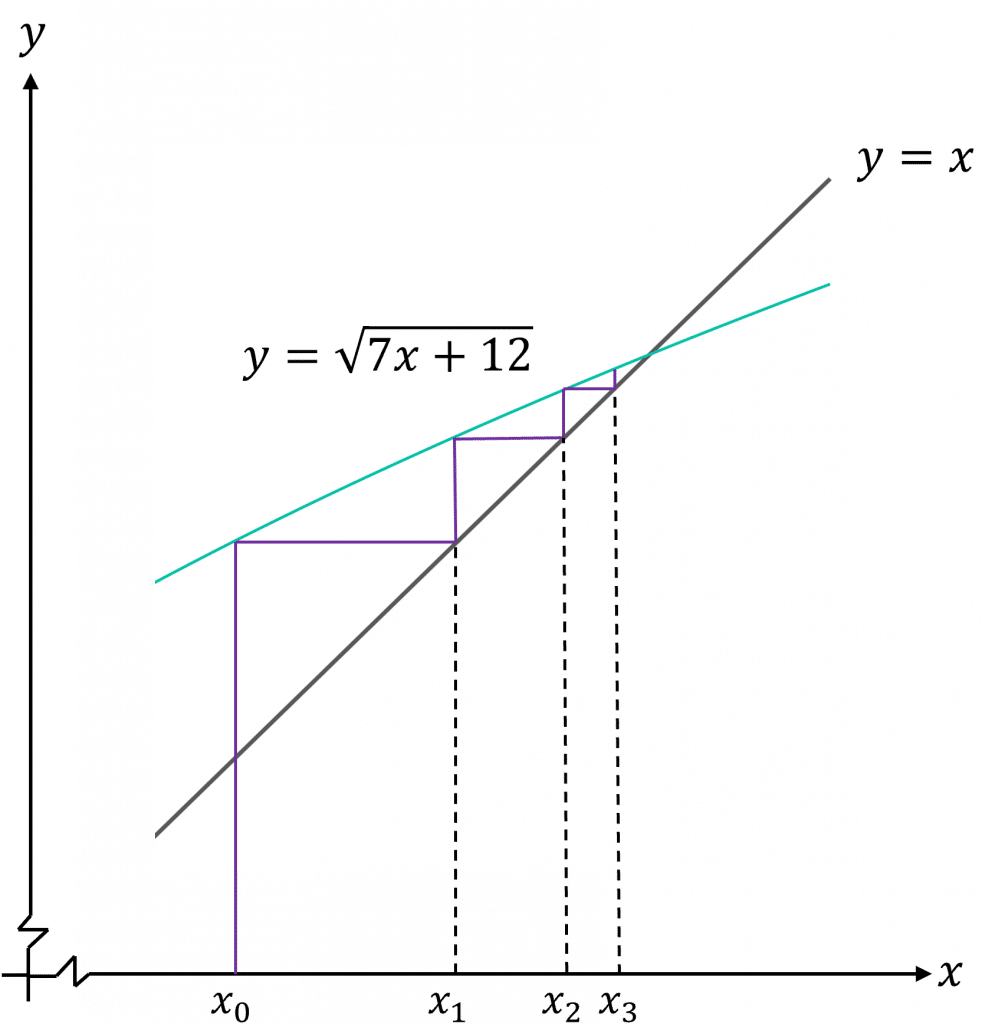
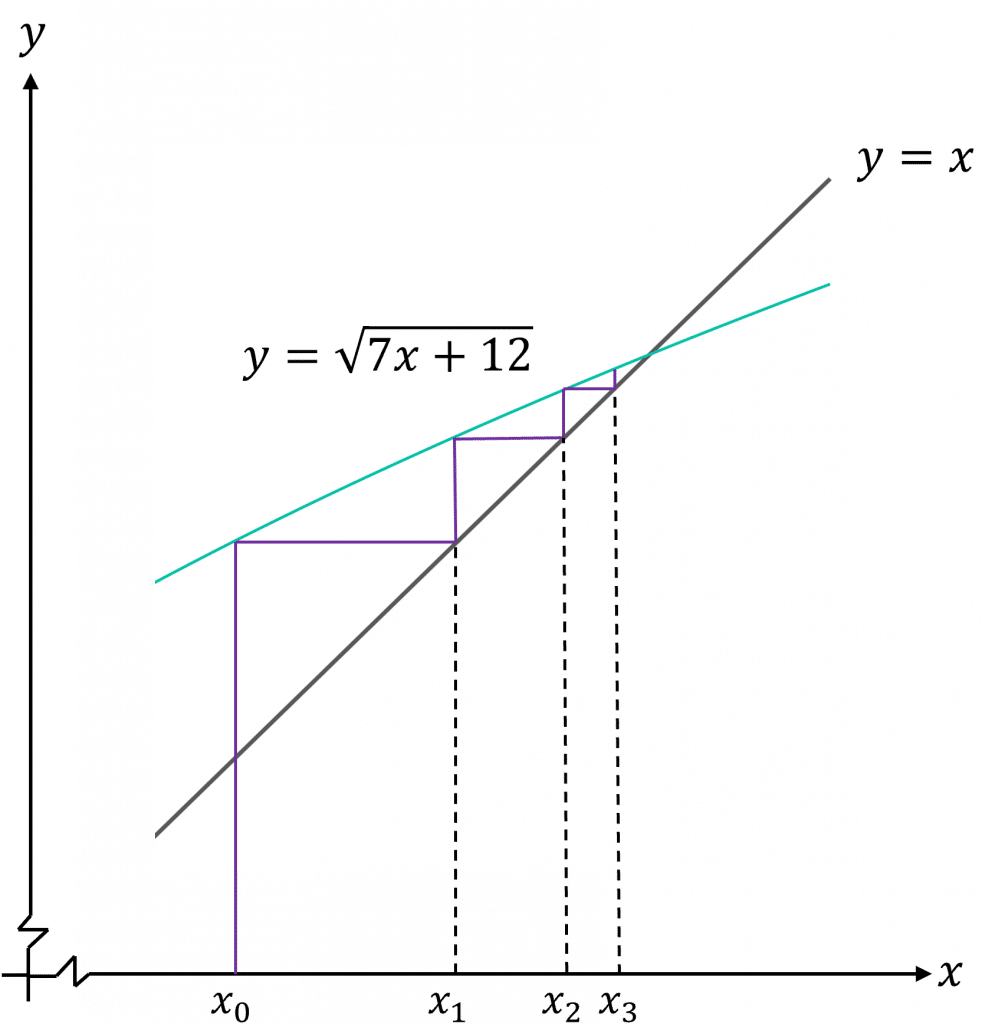
Starting with x_0=8:
x_1=\sqrt{7(8)+12}=8.246211251
x_2=\sqrt{7(8.246211251)+12}=8.350058608
x_3=\sqrt{7(8.350058608)+12}=8.393474266
We can now create the diagram for this iteration formula:
Draw the lines y=x and y=\sqrt{7x+12} on the same set of axis.
Then draw on the lines corresponding with the iterations.
We can see that the sequence is a convergent staircase.
Iterative Methods Example Questions
Example 1: Show that 6x+8-x^2=0 can be rearranged to x=\sqrt{6x+8} and hence start with x_0=7 to find a root to 1 decimal place.
[3 marks]
Add x^2 to both sides of 6x+8-x^2=0:
x^2=6x+8
Then take the square root of each side:
x=\sqrt{6x+8}
Using the iteration formula x_{n+1}=\sqrt{6x_n+8} and x_0=7:
x_1=\sqrt{6(7)+8}=7.071067812
x_2=\sqrt{6(7.071067812)+8}=7.101155319
x_3=\sqrt{6(7.101155319)+8}=7.113854927
Thus, the one approximate root of 6x+8-x^2=0 is 7.1 to 1 decimal place.
Question 2: Use the formula x_{n+1}=\sqrt[3]{7x+11} with x_0=3 to find a root to the equation 11+7x-x^3=0 to 3 decimal places.
[2 marks]
Using x_0=3:
x_1=\sqrt[3]{7(3)+11}=3.174802104
x_2=\sqrt[3]{7(3.174802104)+11}=3.214762996
x_3=\sqrt[3]{7(3.214762996)+11}=3.223760026
x_4=\sqrt[3]{7(3.223760026)+11}=3.225778757
x_5=\sqrt[3]{7(3.225778757)+11}=3.226231368
x_4 and x_5 both round to the same value to 3 decimal places.
So the approximate root is 3.226 to 3 decimal places.
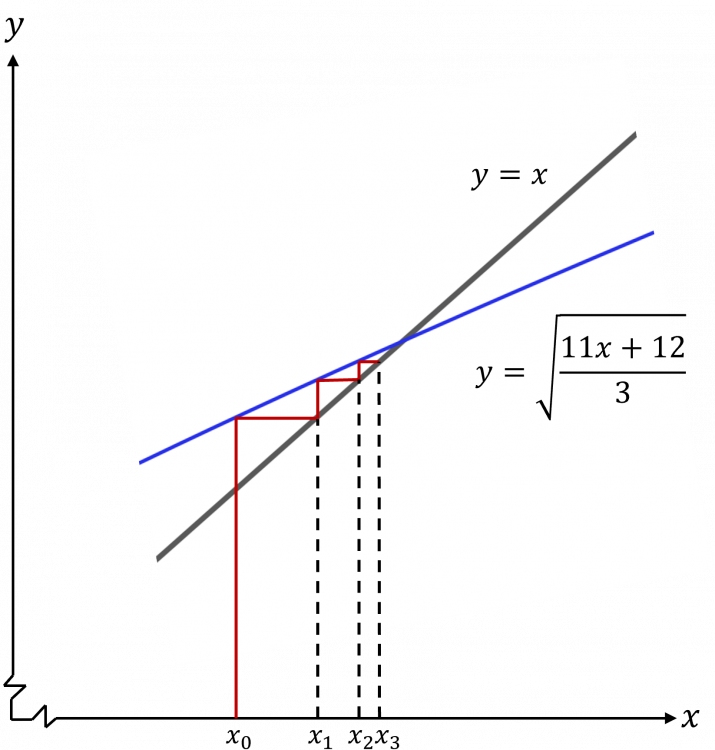
Question 3: The equation 11x-3x^2+12=0 can be rearranged to give the iteration formula:
x_{n+1}=\sqrt{\dfrac{11x+12}{3}}a) Use the iteration formula and x_0=4 to find the root of the equation to 1 decimal place.
b) Sketch a diagram to show the convergence of the sequence for x_1, x_2 and x_3.
[4 marks]
a) Starting with x_0=4:
x_1=\sqrt{\dfrac{11(4)+12}{3}}=4.320493799
x_2=\sqrt{\dfrac{11(4.320493799)+6}{3}}=4.454414731
x_3=\sqrt{\dfrac{11(4.454414731)+6}{3}}=4.509196604
x_2 and x_3 both round to 4.5 to 1 decimal places, so this is our approximate root.
b)
Iterative Methods Worksheet and Example Questions
Newton-Raphson Method and Other Recurrence Relations
A LevelYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






