Locating Roots
Locating Roots Revision
Locating Roots
Sometimes you won’t be able to algebraically solve f(x)=0, so numerical methods will need to be used to give you solutions which are close to the exact solution.
Significance of a Change of Sign Between f(a) and f(b)
If f(a)>0 and f(b)<0 then there is a solution to the equation f(x)=0 between the values a and b. However, this is only true if the function is continuous between a and b, otherwise if it is not, the change in sign might be caused by something other than a root.
Furthermore, if there isn’t a change in sign between two different values of x, this doesn’t necessarily mean there isn’t a root between these values, as the graph of f(x) could just touch the x-axis between these values.
Example:
f(x)=x^3-3x^2-2x+3, show that f(x)=0 has a solution in the interval -1.2 \leq x \leq -1.1
Substitute x=-1.2 and x=-1.1 into f(x):
f(-1.2)=(-1.2)^3-3(-1.2)^2-2(-1.2)+3=-0.648
f(-1.1)=(-1.1)^3-3(-1.1)^2-2(-1.1)+3=0.239
f(-1.2) and f(-1.1) have different signs and f(x) is a continuous function, so there is a solution in the interval [-1.2,-1.1].
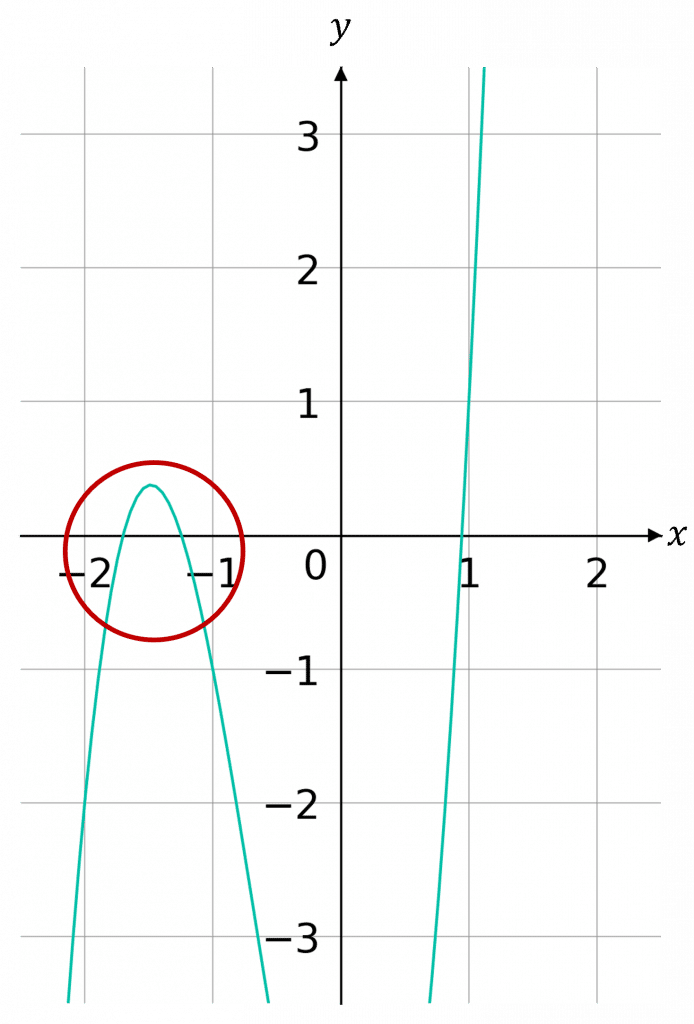

Problems With Large Intervals
When choosing an interval to find roots to an equation, you need to be careful that it is not too large. Large intervals can hide roots if there is an even number of roots in the interval, this is because the sign would change twice within the interval so it would appear to have not changed at all.
If we were trying to find a root for the graph on the right and chose the interval [-2,-1] it would appear that there isn’t a root between these values. However, as we can see by the graph there is definitely a root between -2 and -1, but this wouldn’t be detected by observing the signs of f(-2) and f(-1), as they would both be negative.
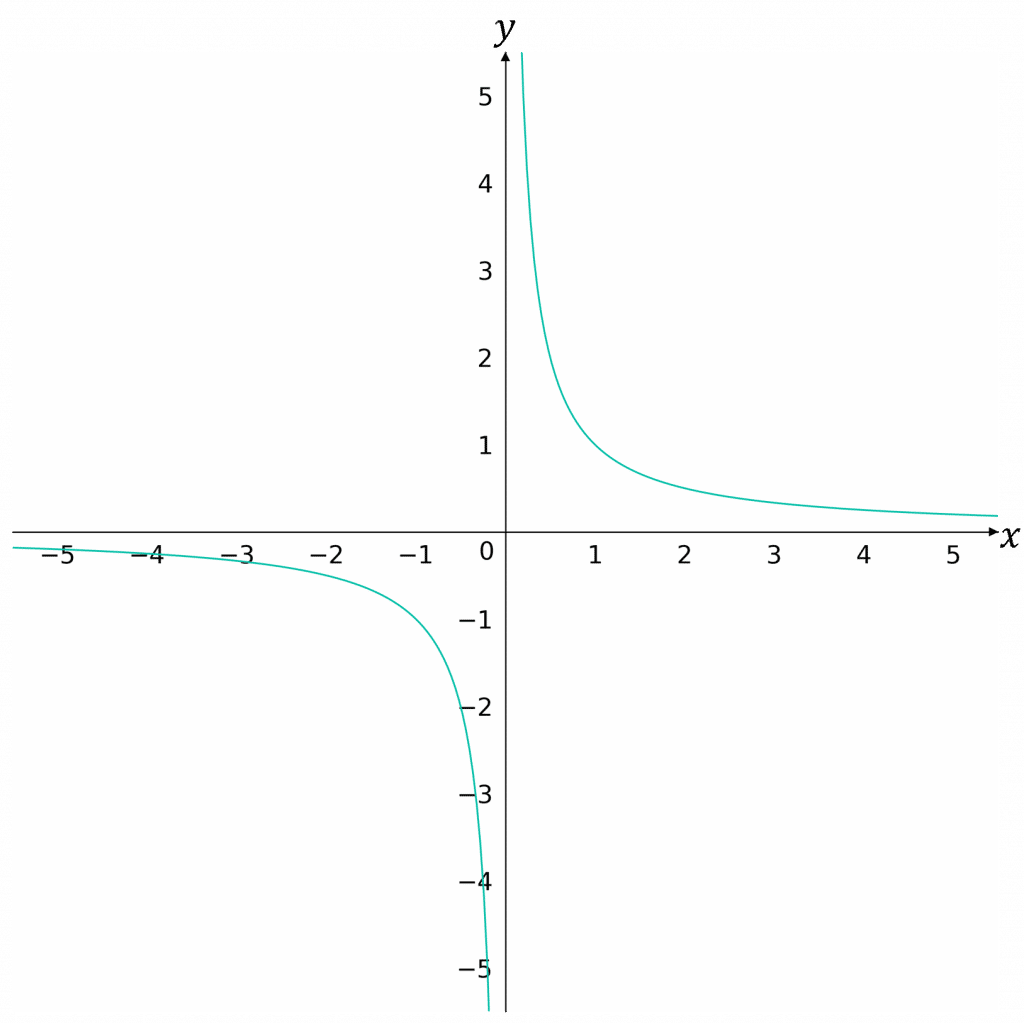

Functions that Aren’t Continuous
If a function isn’t continuous, like the graph of y=\dfrac{1}{x}, there may be sign changes that are not caused by a root.
For example, the graph of y=\dfrac{1}{x} changes sign before and after x=0, however this doesn’t mean x=0 is a root. This sign change is caused by y=\dfrac{1}{x} not being continuous at this point. For this graph, x=0 is an asymptote.
Using Upper and Lower Bounds
Sometimes you will be given an approximation to a root and you’ll be asked to show that this root is correct to a certain accuracy.
To do this you need to show that the root lies in a certain interval, choosing the correct interval is key to this.
Example:
Show that x=0.641 is a root of the equation x^3-5x^2-5x+5=0 to 3 decimal places.
- If x=0.641 is a root of the equation x^3-5x^2-5x+5=0 to 3 decimal places, then the exact root, r, must lie in the upper and lower bounds of this value. So 0.6405 \leq r < 0.6415, as all values in this interval round to our approximate root 0.641 to 3 decimal places.
- A root lies in the interval [0.6405,0.6415) if f(0.6405) and f(0.6415) have different signs. We know this must be true because x^3-5x^2-5x+5=0 is a continuous function.
- f(0.6405)=0.0090576... and f(0.6415)=-0.0011197...
- f(0.6405) and f(0.6415) have different signs so there must be a root between them, and any value between these values round to 0.641 to 3 decimal places, so this root is correct.
Locating Roots Example Questions
Question 1: Show that x=1.594 is a root of x^3-2x^2-5x+9=0 to 3 decimal places.
[3 marks]
The exact root must lie in the interval [1.5935,1.5945), because all values in this interval rounds to 1.594
f(1.5935)=0.000298025375
f(1.5945)=-0.003455466375
f(1.5935) and f(1.5945) have different signs and f(x)=x^3-2x^2-5x+9 is continuous so there must be a root in the interval [1.5935,1.5945), and all values in this interval round to 1.594
Question 2: For the following functions show that there is a root in the interval:
a) (1.6,1.7) for 5-e^x=0
b) (3.25,3.26) for x^3-2x^2-5x+3=0
c) (3.71,3.72) for \ln(x-1)-1=0
[3 marks]
a) 5-e^{1.6}=0.0469675756
5-e^{1.7}=-0.4739473917
So there is a root in the interval (1.6,1.7) due to the sign change and the function being continuous on this interval.
b) (3.25)^3-2(3.25)^2-5(3.25)+3=-0.046875
(3.26)^3-2(3.26)^2-5(3.26)+3=0.090776
So there is a root in the interval (3.25,3.26) due to the sign change and the function being continuous on this interval.
c) \ln(3.71-1)-1=-0.003051365108
\ln(3.72-1)-1=0.0006318803079
So there is a root in the interval (3.71,3.72) due to the sign change and the function being continuous on this interval.
Question 3: The function f(x)=x^4-5x+1
Show that x=1.64 is a solution to f(x)=0 to 2 decimal places.
[3 marks]
The exact root must lie in the interval [1.635,1.645), because all values in this interval round to 1.64
f(1.635)=-0.02886809937
f(1.645)=0.09757130062
f(1.635) and f(1.645) have different signs and f(x)=x^4-5x+1 is continuous so there must be a root in the interval [1.635,1.645), and all values in this interval round to 1.64










