Specific Latent Heat
Specific Latent Heat Revision
Specific Heat Capacity and Specific Latent Heat
If a system is heated and increases in temperature, the amount it increases by depends on the mass, material and energy input of the system. This section will look at the definitions and equations you need to know for specific heat capacity and specific latent heat.
Specific Heat Capacity
The temperature increase of a heated system depends on the mass, the specific heat capacity of the material and the thermal energy input into the system. This is given by the following equation:
\textcolor{aa57ff}{\Delta E = m c \Delta \theta}
- \textcolor{aa57ff}{\Delta E} is the change in thermal energy in joules \left(\text{J}\right).
- \textcolor{aa57ff}{m} is the mass in kilograms \left(\text{kg}\right).
- \textcolor{aa57ff}{c} is the specific heat capacity in Joules per kilogram per degree Celsius \left( \text{J/kg°C} \right).
The specific heat capacity \textcolor{aa57ff}{c} , is the amount of energy needed to increase the temperature of \text{1 kg} of the substance by \text{1°C} .
Different substances have different values of \textcolor{aa57ff}{c} . For example, water has a specific heat capacity of \text{4200 J/kg°C} and aluminium has a specific heat capacity of \text{900 J/kg°C} . Therefore more energy is required to increase the temperature of water (as long as the masses are the same).
Latent Heat
When a change of state happens, energy is required. This energy required to change the state of a substance is called the latent heat.
When a change of state involving heating occurs, such as boiling or melting, this energy supplied to the system increases the internal energy. The substance changes state only and does not change in temperature. This is because the energy is being used to break apart the bonds between particles in the substance, and is not increasing the temperature.
When a change of state involving cooling occurs, such as condensation or freezing, the system decreases in internal energy. This is because energy is being released to make bonds between the particles. Again, the latent heat does not change the temperature, it only changes the state.
Specific Latent Heat
Specific Latent Heat is the energy required to change the state of \text{1 kg }of of a substance. The formula is:
\textcolor{00bfa8}{E = m L}
- \textcolor{00bfa8}{E} is the energy needed or released in Joules \left(\text{J}\right).
- \textcolor{00bfa8}{m} is the mass of the substance in kilograms \left(\text{kg}\right).
- \textcolor{00bfa8}{L} is the specific latent heat of a substance in Joules per kilogram \left(\text{J/kg}\right).
Specific latent heat has different names for different changes of state.
Specific latent heat of fusion – the specific latent heat for a change from a solid to a liquid.
Specific latent heat of vaporisation – the specific latent heat for a change from a liquid to a vapour (gas).
Heating and Cooling graphs
The process of a substance changing state or increasing in temperature can be shown in a heating or cooling graph.
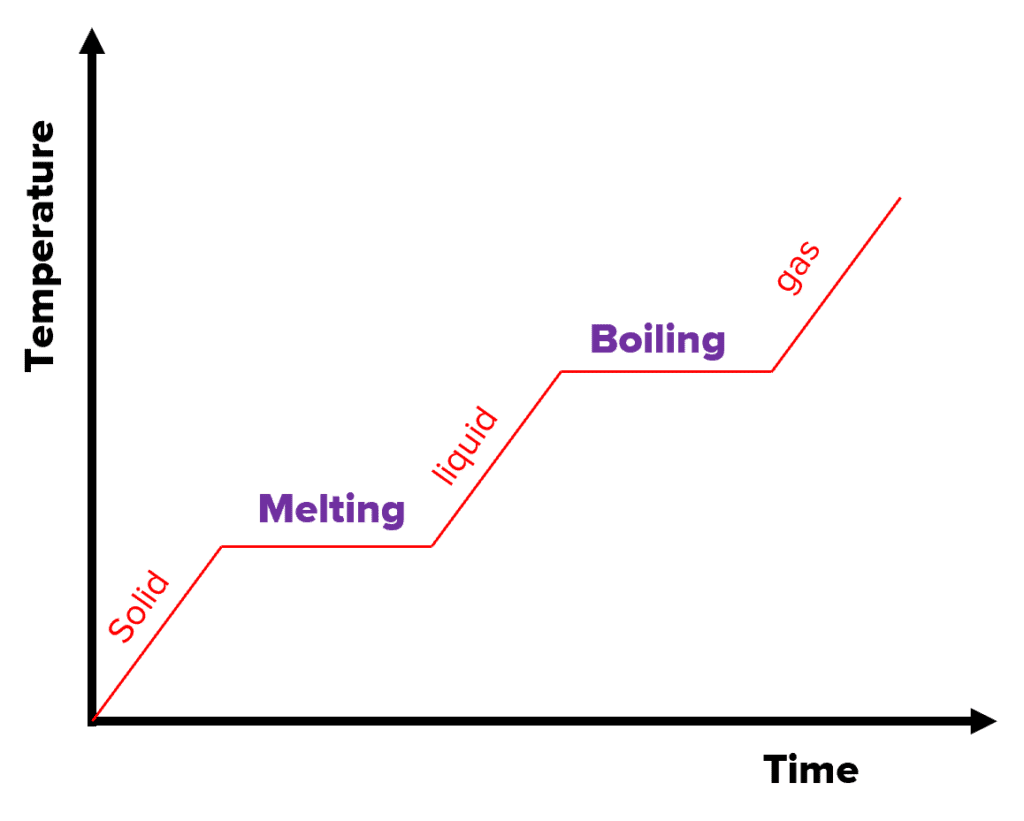
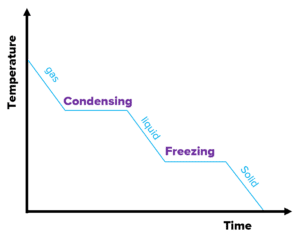
The graph on the right is a heating graph. As the substance is heated over time, the temperature increases. However, notice the flat sections of the graph. This is where the substance is changing state.
As mentioned, when changing state, latent heat is involved and hence the temperature stays constant. The internal energy increases because there is an energy input into the system, but no energy is used to raise the temperature.
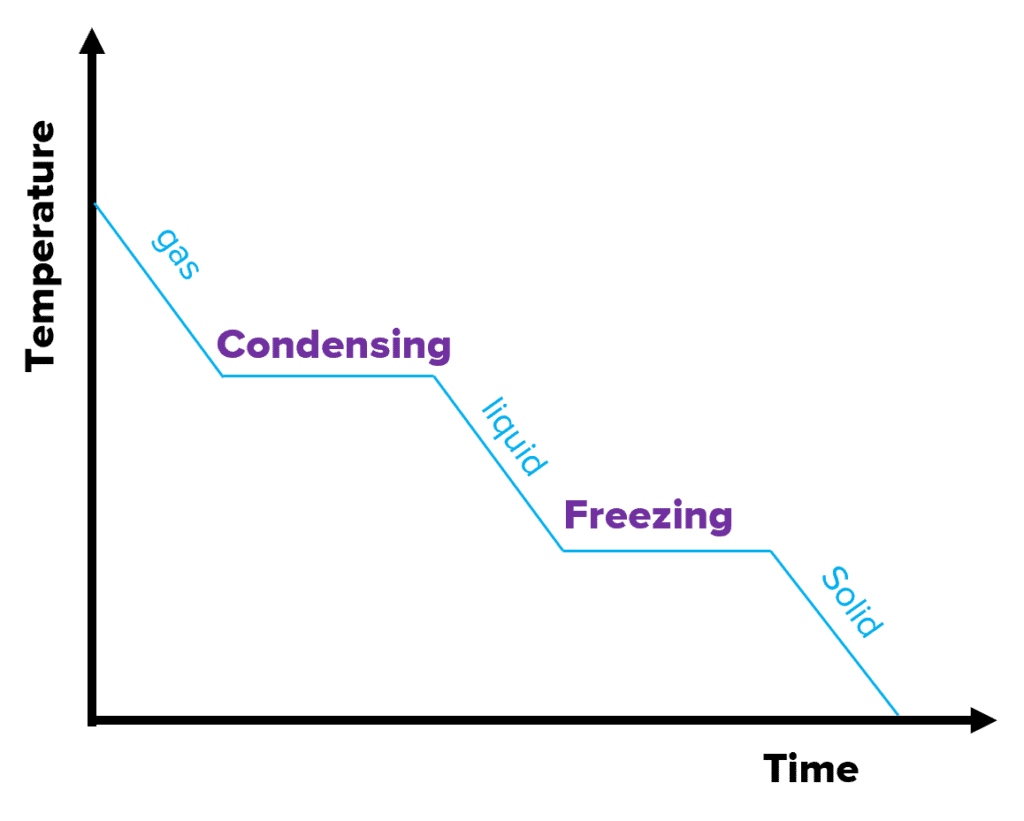
The graph on the right is a cooling graph. As the substance is cooled over time, the temperature decreases. The flat sections again show where the substance is changing state at a constant temperature. The internal energy decreases because energy is being released during cooling.
Specific Latent Heat Example Questions
Question 1: State the definition of latent heat.
[2 marks]
Latent heat is the energy required (or released) during a change of state of a substance.
Question 2: A student heats up a beaker of \text{0.7 kg} of water using a bunsen burner. The water increases temperature from \text{25°C} to \text{100°C}. What is the change in thermal energy of the water?
Specific heat capacity of water =\text{4200 J/kg°C}
[3 marks]
Change in temperature = \bold{100°C - 25°C = 75°C}
\Delta E = m c \Delta \theta
\bold{\Delta E = 0.7 \times 4200 \times (75)}
\bold{\Delta E = 220500} \: \textbf{J}
Question 3: A pot of \text{7 kg} of water is heated to \text{100°C} and starts to boil. What is the energy required for the water to evaporate? Give your answer in kilojoules \left(\text{kJ}\right).
Specific latent heat of fusion for water is \text{3340 kJ/kg}
[2 marks]
E = m L
\bold{E = 7 \times 3340}
\bold{E = 23380 \: \textbf{kJ}}
Question 4: What type of process is this graph representing?
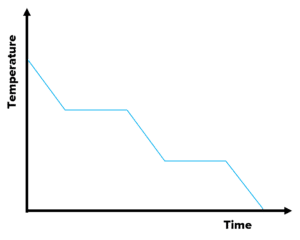
Label the graph with each state and change of state.
[3 marks]