Density
Density Revision
Density
Density measures how compact a substance is. It relates how much mass a substance has to the volume that it takes up. Different materials have different densities.
Density
Density is defined as an object or substances mass per unit volume. This can be seen in the density equation:
\textcolor{aa57ff}{\text{Density} = \dfrac{\text{Mass}}{\text{Volume}}}
This can also be written as:
\textcolor{aa57ff}{\rho = \dfrac{m}{V}}
- \textcolor{aa57ff}{\rho} is the Density in kilograms per metre cubed \left(\textcolor{aa57ff}{\textbf{kg/m}^{3}}\right) .
- \textcolor{aa57ff}{m} is the Mass in kilograms \left(\textcolor{aa57ff}{\textbf{kg}}\right).
- \textcolor{aa57ff}{V} is the Volume in metres cubed \left(\textcolor{aa57ff}{\textbf{m}^3 }\right).
An object with particles in a closer arrangement will have a higher density. So a solid will be more dense than a liquid and a gas.
Required Practical
Measuring the density of regular and irregular objects
Calculating the density of some objects is easier than others, depending on how easy it is to calculate the shape’s volume. For example, calculating the volume of an object with a regular shape, like a box, is a lot easier than calculating the volume of an irregular shaped object like a rock.
Doing the experiment
For regular objects, like a box, finding the density is very simple:
- Measure the length, width and height of the box and multiply them together to get the volume.
- Place the box on a balance to find the mass of the box.
- Use the mass and volume in the density equation \left( \rho = \dfrac{m}{V} \right) to calculate the density of the rock.
For irregular objects, a displacement technique can be used to measure the volume and calculate the density:
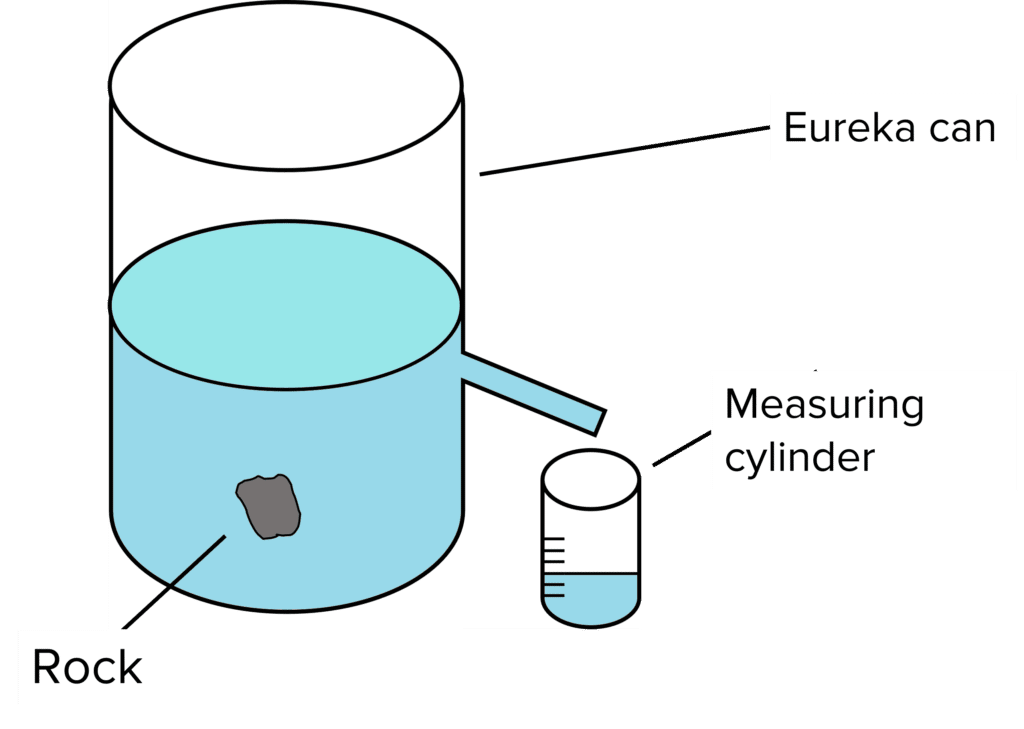
- Use a balance to measure the mass of the object (in this case it is a rock).
- To find the volume of the rock, set up a eureka can filled with water just up until the spout.
- Place a measuring cylinder underneath the spout, and place the rock in the eureka can. The rock will displace water into the measuring cylinder.
- Record the volume of water in the measuring cylinder because this is the volume of the rock.
- Use the mass and volume in the density equation \left( \rho = \dfrac{m}{V} \right) to calculate the density of the rock.
Example: Calculating Density
A solid metal cube has a mass of \text{\textcolor{10a6f3}{5 kg}} and sides of length \text{\textcolor{00bfa8}{0.5 \: m}} . Calculate the density of the metal cube.
[2 marks]
Find the volume of the cube by multiplying the length of each side:
\textcolor{00bfa8}{0.5} \times \textcolor{00bfa8}{0.5} \times \textcolor{00bfa8}{0.5} =0.125 \: \text{m}^3
Using \rho = \dfrac{m}{V} = \dfrac{\textcolor{10a6f3}{5}}{0.125}
\rho = 40 \: \text{kg/m}^3
Density Example Questions
Question 1: A rock has a mass of \text{0.6 kg} and a volume of \text{0.15 m}^3 . Calculate it’s density.
[2 marks]
Using \bold{\rho = \dfrac{m}{V} = \dfrac{0.6}{0.15}}
\bold{\rho = 4} \: \textbf{kg/m}^3Question 2: A cube box has a density of \text{25 kg/m}^3 and a mass of 8 \: \text{ kg} .
Calculate the length of each side of the box.
[3 marks]
We know that the box is a cube so:
length of sides = \bold{\sqrt[3]{V} = \sqrt[3]{0.32} = 0.68} \: \textbf{m} \text{ (2 sf)}
Question 3: A student wants to find out the density of a rock. Describe an experiment they could perform to determine the density of this rock.
[6 marks]
Because it is an irregularly shaped object, we cannot just measure the dimensions to find the volume.
- First, fill up a eureka can just up to the spout.
- Set up a measuring cylinder to catch any water that comes out of the spout.
- Use a balance to record the mass of the rock, and the place the rock into the water.
- The volume of the water in the measuring cylinder is the same as the volume of the rock. Record this volume.
- Use \rho = \dfrac{m}{V} to find the density of the piece of rock.







