Potential Difference and Resistance
Potential Difference and Resistance Revision
Potential Difference and Resistance
As well as current, we can also measure the potential difference (pd) of a circuit and the resistance of a circuit.
Definitions
Potential difference is the driving force that causes electric charges to flow around a circuit. The units of potential difference are Volts (\text{V})and it can be measured using a voltmeter. A voltmeter must be connected in parallel with the component for which you want to know the potential difference.
Resistance slows down the flow of electrical charges in a circuit. The units of resistance are Ohms (\Omega).
Current, potential difference and resistance are related by the following equation:
\color{aa57ff}{V=IR}
- V= the potential difference in volts \text{(V)}
- I = the current in amps \text{(A)}
- R = the resistance in Ohms (\Omega).
Required Practical
Investigating Factors Affecting Resistance of Electrical Circuits
There are many different ways of altering the current and potential difference of a circuit. In this experiment, you can investigate the effects of changing the length of a wire.
Doing the experiment
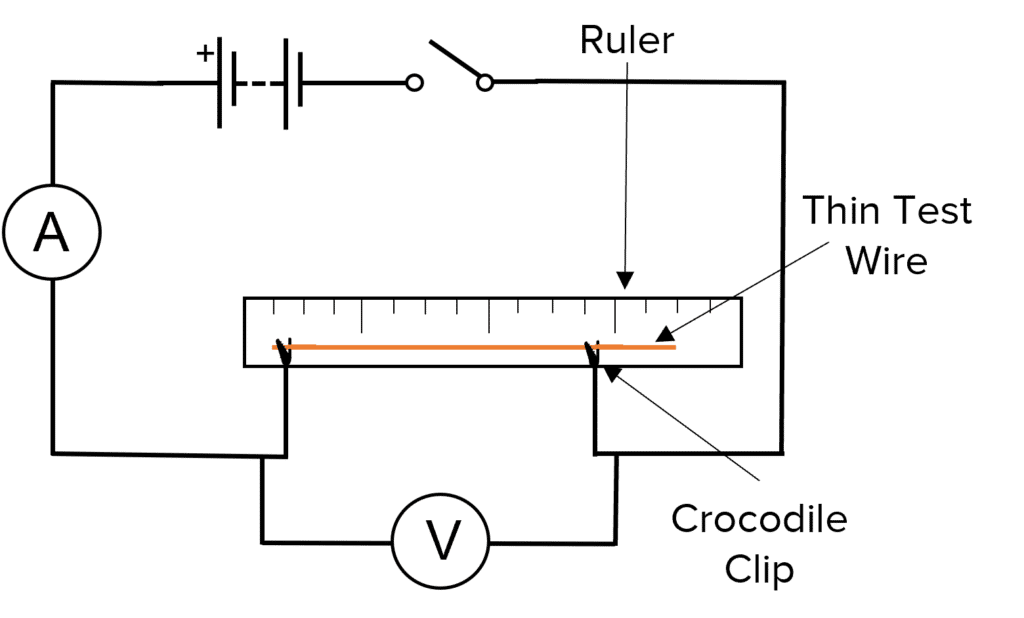
- Set up a circuit as shown in the circuit diagram.
- Using the ruler, measure the distance between the two crocodile clips. This is the “wire length”.
- Close the switch and record the current on the ammeter and the potential difference on the voltmeter.
- Move the claw clips so that the wire length is bigger or smaller. Repeat the measurements of length, current and potential difference.
- Repeat the experiment for a number of different wire lengths.
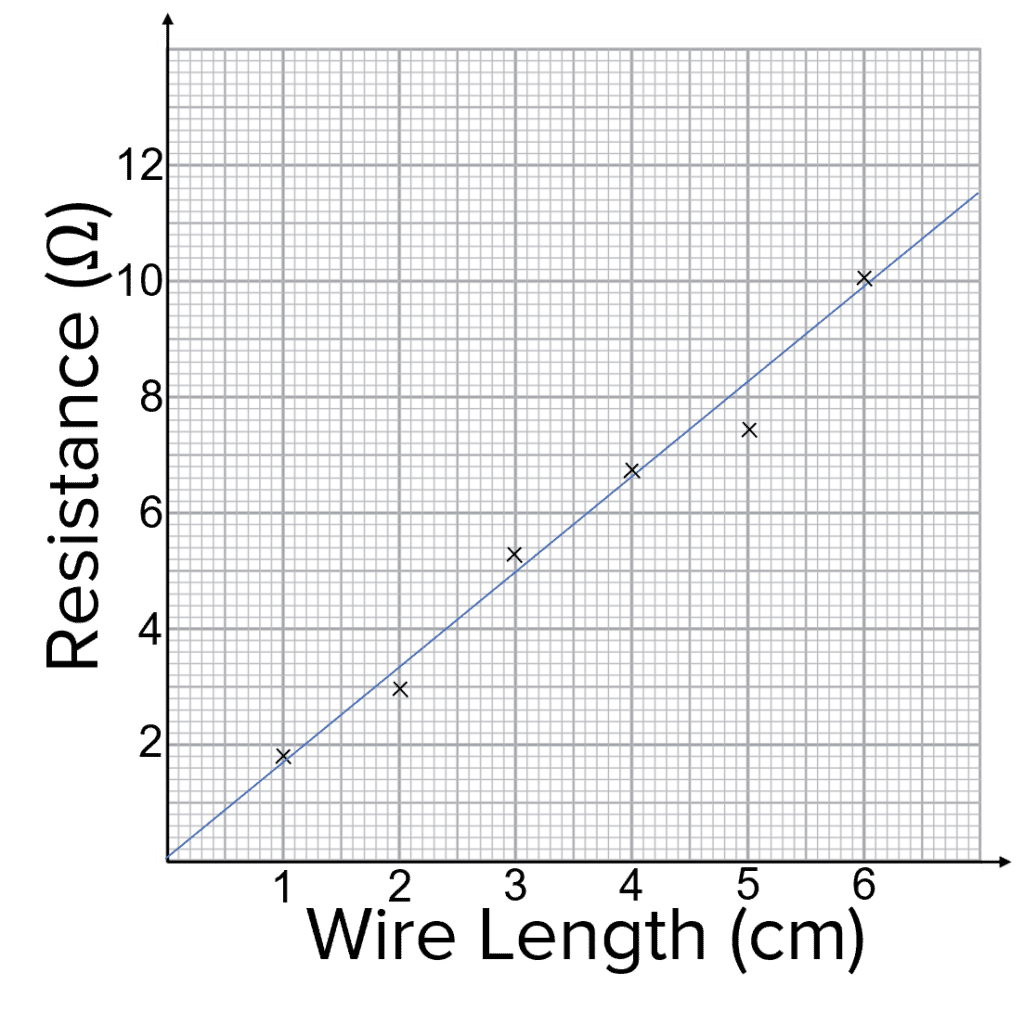
You can now use your results to test the relationship between resistance and the wire length.
- Rearrange \text{V}=\text{IR} to get \text{R}=\dfrac{\text{V}}{\text{I}} and use this equation to calculate the resistance of the wire for each wire length.
- Plot the resistance versus the wire length.
- Draw a line of best fit. This should be a straight line that passes through the origin of the graph.
- The line of best fit shows that the resistance is directly proportional to the wire length.
You can also alter this experiment to investigate the effect of adding resistors in series and parallel.
Example: Calculating Current from Potential Difference and Resistance
The potential difference across a 20 \Omega resistor is 8\text{ V}. What is the current across the resistor?
[2 marks]
\bold{\text{V}=\text{IR}}so
\begin{aligned}I&=\dfrac{\text{V}}{\text{R}}\\&=\dfrac{\textcolor{2730e9}{8}}{\textcolor{7cb447}{20}}=\bold{0.4\text{ A}}\end{aligned}
Potential Difference and Resistance Example Questions
Question 1: Define resistance.
[1 mark]
A property that slows down the flow of electrical charge (or current).
Question 2: Describe how you might measure the potential difference across a lamp.
[2 marks]
Connect a voltmeter to the lamp in parallel.
Question 3: The current across a 4\Omega resistor is 3\text{ A}. What is the potential difference across the resistor?
[2 marks]
Question 4: Describe an experiment you could do to investigate the effect of the length of a wire on resistance. Use a circuit diagram to help your description.
[6 marks]
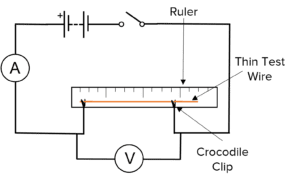
Set up a circuit as shown in the circuit diagram. Using the ruler, measure the distance between the two crocodile clips. This is the “wire length”. Close the switch and record the current on the ammeter and the potential difference on the voltmeter. Move the crocodile clips so that the wire length is bigger or smaller. Repeat the measurements of length, current and potential difference and then repeat the experiment for a number of different wire lengths.