Volume of 3D Shapes
Volume of 3D Shapes Revision
Volume of 3D Shapes
The volume of a 3D shape is how much space it takes up. You are expected to know how to work out the volumes of different shapes, some of these will come with a formula attached to the question and some won’t:
- You will have to remember how to find the volumes of: prisms and pyramids.
- You will be given the formulae for finding the volumes of: cones and spheres.
Make sure you are happy with the following topics before continuing:
Volume of Cubes and Cuboids
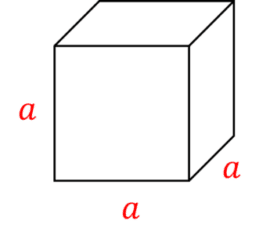

The volume of a cube is the length of one side of the cube multiplied by itself three times:
\text{Volume of cube}=\textcolor{red}{a}\times \textcolor{red}{a}\times \textcolor{red}{a}=\textcolor{red}{a}^{3}
where \textcolor{red}{a} is the length of one side.
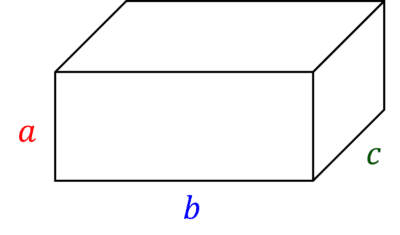

The volume of a cuboid is the product of the three different side lengths:
\text{Volume of cuboid}=\textcolor{red}{a}\times \textcolor{blue}{b}\times \textcolor{green}{c}
where \textcolor{red}{a}, \textcolor{blue}{b} and \textcolor{green}{c} are the three different side lengths of the cuboid.
Volume of Prisms
The formula for the volume of a prism is:
\text{Volume of prism }=\textcolor{red}{\text{ area of cross section }}\times\textcolor{blue}{\text{ length}}
This is for any prism, including cuboids & cylinders, and you do have to remember this formula.
So, for Cylinders it would be:
V = \textcolor{red}{\pi r^2 } \times \textcolor{blue}{\text{ length}}
Example: Below is a triangular prism. The triangular face has base 6 cm and perpendicular height 5 cm.
The prism has length 3.5 cm.
Work out the volume of the shape.
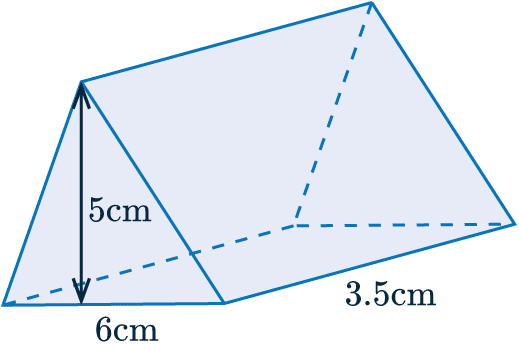
In this case, the cross section is a triangle, so we need to multiply the area of the triangle by the length. We get:
\text{Area of cross section }=\textcolor{red}{\dfrac{1}{2}\times5\times 6}=\textcolor{red}{15}\text{ cm}^2
Therefore,
\text{Volume of the prism }=\textcolor{red}{15}\times \textcolor{blue}{3.5}=52.5\text{ cm}^3.
Volume of Pyramids and Cones
The formulas for the volume of pyramids and cones are:
\text{Volume of pyramid }=\dfrac{1}{3}\times\textcolor{red}{\text{ area of base }}\times\textcolor{blue}{\text{ perpendicular height}}
\text{Volume of cone }=\dfrac{1}{3} \times \textcolor{red}{\pi r^2} \times \textcolor{blue}{\text{ perpendicular height}}
Example: Below is a square-based pyramid.
The base has side-length 14 mm and the pyramid has perpendicular height 25 mm.
Work out the volume of the pyramid.
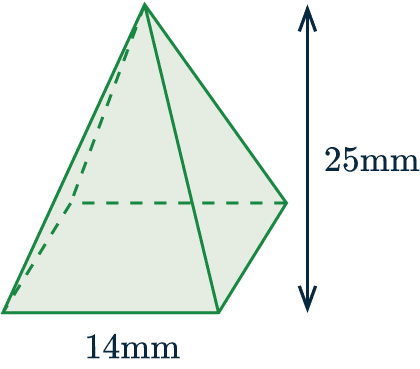
For this question we have a square base, so we have to find one third of the area of the square times by the height.
We get:
\text{Area of base }= \textcolor{red}{14^2}= \textcolor{red}{196}\text{ mm}^2
Therefore,
\text{Volume of the pyramid }=\dfrac{1}{3} \times \textcolor{red}{196}\times\textcolor{blue}{25}=1633.3 \text{ mm}^3
Volume of a Sphere
The formula for the volume of a sphere is:
\text{Volume of a sphere} = \dfrac{4}{3}\textcolor{red}{\pi} \textcolor{blue}{r}^3
Example: Below is a sphere with radius \textcolor{blue}{4} cm
Calculate the volume of the sphere.
Give your answer to 3 significant figures.
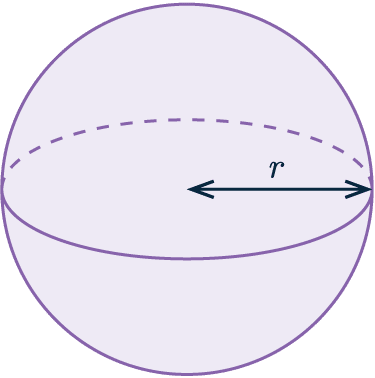
We know the radius of the sphere is 4 cm, so we need to input this into the formula.
Volume of a sphere = \dfrac{4}{3} \textcolor{red}{\pi} (\textcolor{blue}{4})^3 = 268 \text{ cm} ^3 (3 sf)
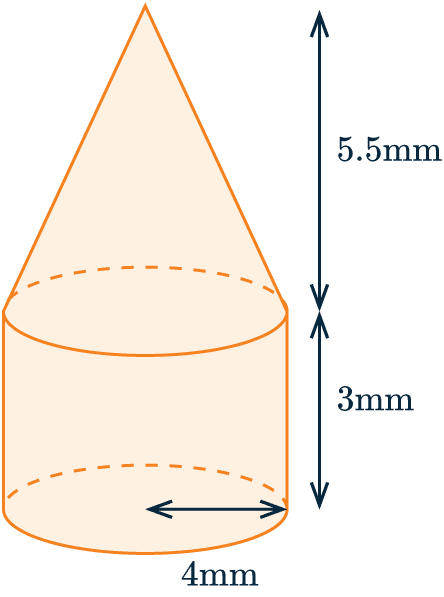
Example: Composite Shape
The shape below was made by attaching a cone to the top of a cylinder.
The base of the cylinder has radius 4 mm, the height of the cylinder portion is 3 mm, and the height of the cone portion is 5.5 mm.
Calculate the volume of the whole shape.
[4 marks]

So, to work out the volume of the shape, we need to work out the two volumes separately.
Firstly, the cylinder is a type of prism, so we calculate the following:
\text{volume of cylinder}=\pi\times4^2\times3=48\pi
Next, we have to work out the volume of the cone:
The vertical height = 5.5 mm and the radius = 4 mm.
Therefore, we get
\text{volume of cone }=\dfrac{1}{3}\pi\times4^2\times5.5=\dfrac{88}{3}\pi
Then, the volume of the shape is the sum of these two answers:
\text{volume of whole shape }=48\pi+\dfrac{88}{3}\pi
= 242.9498...=242.9\text{ mm}^3\text{ (1 dp)}
Volume of 3D Shapes Example Questions
Question 1: The diagram shows the outline of a cuboid, ABCDEFGH. Given that: AB=3 cm, BC=12 cm, and CF=16 cm. Find the volume of the cuboid.
[3 marks]
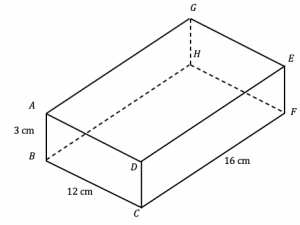
To find the volume we simply have to multiply all three lengths together:
\text{volume}= 3\times12 \times16=576\text{cm}^3
Question 2: The diagram shows the outline of a square based pyramid, ABCDE. The vertical height of the pyramid is 12 m and the base length, CD, is 5 m. Find the volume of the square based pyramid.
[3 marks]
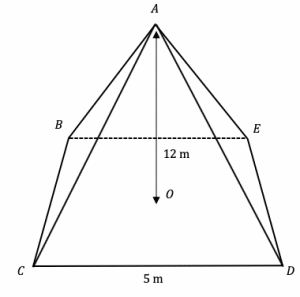
The volume of a square base pyramid is given by the following formula:
\text{volume}= \dfrac{1}{3} \times \text{base area} \times \text{height}
Substituting the values given in the question into the equation above, we find that,
\text{volume}= \dfrac{1}{3} \times 5^{2} \times 12 =100 \text{m}^3
Question 3: Below is a trapezoidal prism. The trapezium’s parallel sides have lengths 45 cm and 60 cm and its perpendicular height is 20 cm. The length of the prism is 80 cm. Work out the volume of the prism.
[3 marks]
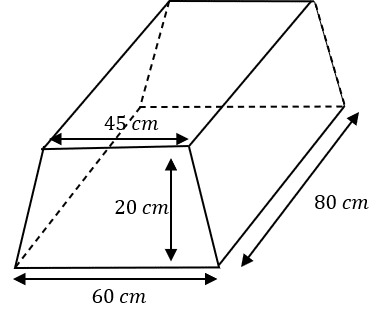
So, to work out the volume of a prism we must multiply the area of the cross section by the length. In this case, the cross section is a trapezium, and the area of the trapezium is:
\text{area of cross section }=\dfrac{1}{2}\times(45+60)\times20= 1,050\text{ cm}^2
The length of the prism is 80 cm, so we get:
\text{volume of prism }=1,050\times80=84,000\text{ cm}^3
Question 4: Below is a triangle-based pyramid. The base of the pyramid has area 18 cm^2 and the height of the pyramid is x+5 cm^2. The volume of the pyramid is 54 cm^2. Work out the value of x.
[4 marks]
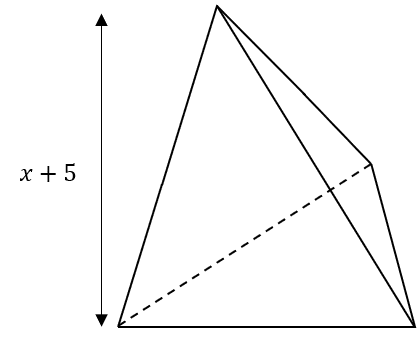
This may seem a little different, but it actually comes up a lot.
First, we must write the volume in terms of x. The volume of a pyramid is one third of the area of the base times by the perpendicular height. We know the area of the base is 18\text{cm}^2, and the expression we’re given for the height is x+5, so the volume is
\dfrac{1}{3}\times18\times(x+5)=6(x+5)
Now, the question also gave us the volume: 54\text{cm}^3, so we can equate this value to the expression we found above and voila, we have an equation:
6(x+5)=54
Now, we solve this equation to find x. First, divide both sides by 6 to get:
x+5=54\div6=9
Then, subtracting 5 from both sides we get the answer to be:
x=9-5=4\text{cm}
Question 5: The composite shape below was made by attaching a hemisphere (half of a sphere) to the top of a cylinder. The base of the cylinder is 2.3 m and the height of the cylinder is 5.6 m. The formula for the volume of a sphere is \dfrac{4}{3}\pi r^3 . Work out the volume of the whole shape to 3 significant figures.
[4 marks]
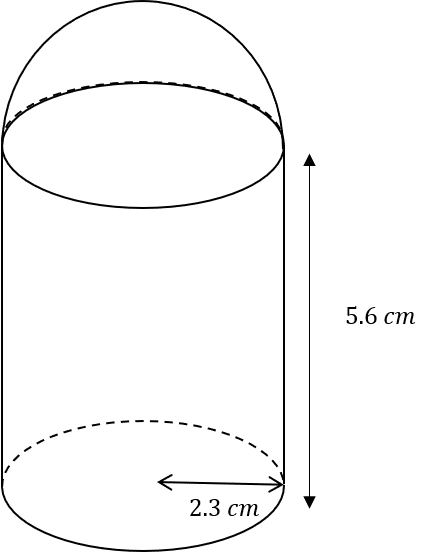
We will work out the volume of the cylinder first, then the hemisphere, and add together the values.
A cylinder is a prism which means that to find the volume, we must multiply the area of the circular cross section by its length. The radius of the circle is 2.3m and the length is 5.6m, so we get:
\text{volume of cylinder }=\pi \times (2.3)^2\times5.6 \approx 93.07 \text{m}^3
Note: Keep the full answer stored in the calculator for adding it to the other value at the end.
Next, we are given the formula for the volume of a sphere, so to find the volume of the hemisphere we will use this formula and then half the result. The radius of the hemisphere is the same as that of the cylinder, 2.3, so we get:
\text{volume of hemisphere }=\dfrac{1}{2}\times\left(\dfrac{4}{3}\pi\times(2.3)^3\right)\approx 25.48\text{m}^3
Therefore, the total volume of the shape is:
93.0665...+25.4825...=119\text{ m}^3 \text{ (3s.f.)}
Volume of 3D Shapes Worksheet and Example Questions
(NEW) Volume of 3D Shapes Exam Style Questions - MME
Level 4-5GCSENewOfficial MMEVolume of 3D Shapes Drill Questions
Perimeter Area Volume - Drill Questions
Level 1-3GCSEArea and Volume - Drill Questions
Level 4-5GCSEVolume And Surface Area Of Cylinder - Drill Questions
Level 4-5GCSEVolume Of Prism - Drill Questions
Level 4-5GCSEVolume of Shapes - Drill Questions
Level 1-3GCSE
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now



