Surface Area of 3D Shapes
Surface Area of 3D Shapes Revision
Surface Area
The surface area of a 3D shape is a measure of how much area the surfaces of that shape have in total.
Shapes that you have to work out the surface area of can fall into one of two categories.
– All the faces are flat – e.g. square or rectangle.
– Some/all of the faces are curved – e.g. cone or sphere.
Make sure you are happy with the following before continuing:
Surface Area of Cubes and Cuboids
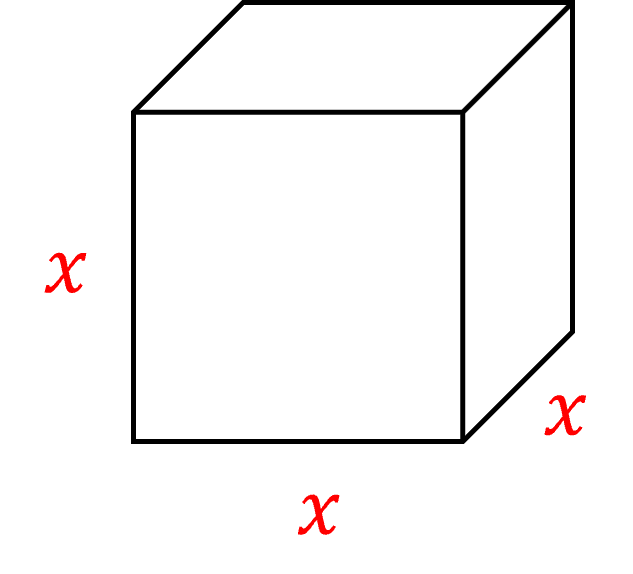

A cube is made of \textcolor{blue}{6} identical square faces.
If a cube has a side length of \textcolor{red}{x}, then each of these faces are squares with side lengths \textcolor{red}{x}.
So the area of one face is \textcolor{red}{x}\times\textcolor{red}{x}=\textcolor{red}{x}^{2}
Hence, the surface area of the whole cube is \textcolor{blue}{6} times this, or \textcolor{blue}{6}\textcolor{red}{x}^{2}
\text{Surface Area of a Cube}=\textcolor{blue}{6}\textcolor{red}{x}^{2}
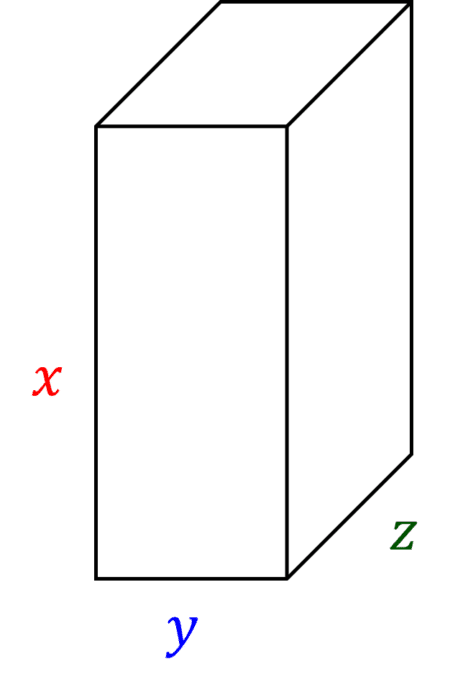

A cuboid is made of 6 rectangular faces.
Opposite rectangular faces are equal, meaning that we have 3 pairs of differently sized rectangles.
If the cuboid has sides \textcolor{red}{x}, \textcolor{blue}{y} and \textcolor{green}{z}, then…
Two of the rectangles have sides \textcolor{red}{x} and \textcolor{blue}{y}\\
Two of the rectangles have sides \textcolor{red}{x} and \textcolor{green}{z}\\
Two of the rectangles have sides \textcolor{blue}{y} and \textcolor{green}{z}
This gives rectangle areas of \textcolor{red}{x}\textcolor{blue}{y}, \textcolor{red}{x}\textcolor{green}{z} and \textcolor{blue}{y}\textcolor{green}{z}
Since there are 2 of each of these rectangles, the total surface area is 2(\textcolor{red}{x}\textcolor{blue}{y}+\textcolor{red}{x}\textcolor{green}{z}+\textcolor{blue}{y}\textcolor{green}{z})
\text{Surface Area of a Cuboid}=2(\textcolor{red}{x}\textcolor{blue}{y}+\textcolor{red}{x}\textcolor{green}{z}+\textcolor{blue}{y}\textcolor{green}{z})
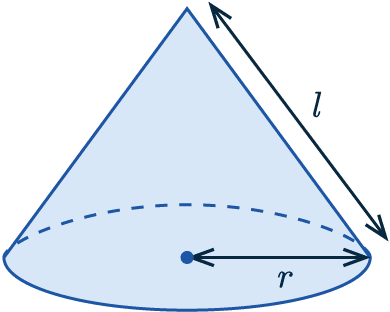
Surface Area of a Cone

Surface area = \pi \textcolor{blue}{r}\textcolor{red}{l} + \pi \textcolor{blue}{r}^2
Where \textcolor{blue}{r} is the radius of the cone.
\textcolor{red}{l} is the slanted height of the cone.
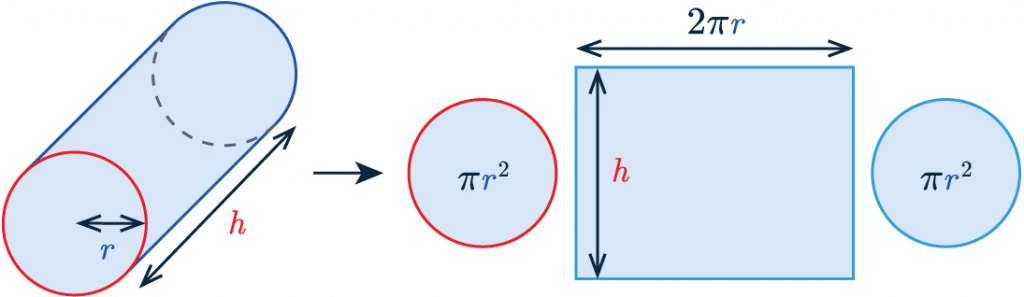
Surface Area of a Cylinder

Surface area = 2\pi \textcolor{blue}{r} \textcolor{red}{h} + 2 \pi \textcolor{blue}{r}^2
Where \textcolor{blue}{r} is the radius of the cylinder.
\textcolor{red}{h} is the height of the cylinder.
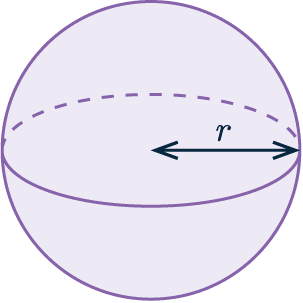
Surface Area of a Sphere

Surface area = 4\pi \textcolor{blue}{r}^2
Where \textcolor{blue}{r} is the radius of the sphere.
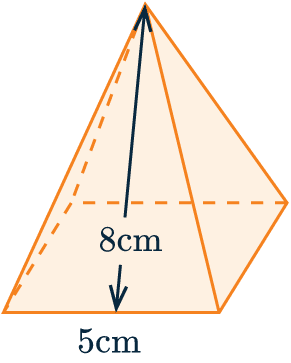
Example 1: Surface Area of a Square Based Pyramid
Find the surface area of the square based pyramid shown:
[3 marks]

All 4 of its triangular faces are identical.
We only need to work out the area of one and then multiply it by 4 to get the area of them all.
Area of a triangle is \frac{1}{2}bh, and here the base is 5 cm and the height is 8cm.
\dfrac{1}{2}\times5\times8=20\text{ cm}^2
Therefore, the area of all 4 triangles is
4\times20=80\text{ cm}^2.
Next we need to add the area of the square base to the total area.
Area of base = 5^2=25\text{ cm}^2
Therefore,
Total surface area =25+80=105\text{ cm}^2
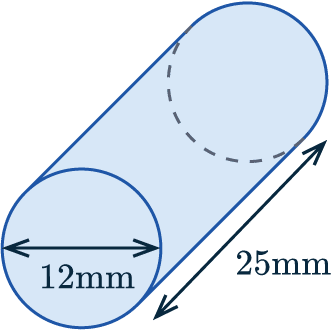
Example 2: Surface Area of a Cylinder
Find the surface area of the cylinder, giving your answer to 4 significant figures.
[3 marks]

We know the formula for the surface area of a cylinder is
Surface area = 2\pi r h + 2\pi r^2
From the diagram we can see:
– the radius, r, = 12\div 2 = 6 mm
– the height of the cylinder is 25 mm
We can then apply these to the equation:
(2 \times \pi \times 6 \times 25 ) + ( 2 \times \pi \times 6^2)
Surface area = 300\pi + 72\pi = 1169 \text{ mm}^2
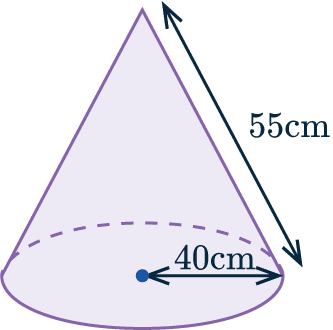
Example 3 : Surface Area of a Cone
Calculate the surface area of the cone shown:
[3 marks]

The formula for the surface area of a cone is
Surface area of a cone = \pi r^2+\pi rl
Where r is the radius of the base and l is the slant height.
Therefore, the surface area of this cone is
\pi\times 40^2+\pi\times40\times55=11938.1\text{ cm}^2\text{ (1 dp)}
Example 4: Surface Area of a Sphere
A sphere with surface area 1,025\text{ m}^2 is shown.
Work out the length of the radius.
Give your answer to 2 significant figures.
[3 marks]
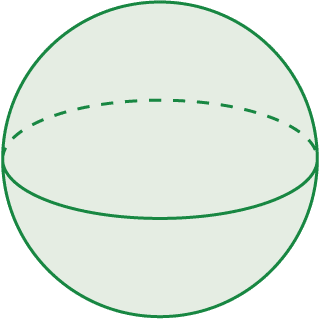
The formula for the surface area of a sphere is
Surface area of a sphere \, = 4\pi r^2
We know that the surface area is 1025 m^2, so we can set the formula above equal to 1025 to get
4\pi r^2=1025
Then, if we divide both sides by 4\pi, we get
r^2=1025\div4\pi=81.5669...
Finally, square rooting this we get
r=\sqrt{81.5669...}=9.0\text{ m} \text{ (2 sf)}
Surface Area of 3D Shapes Example Questions
Question 1: Below is a cuboid with length 6 mm, width 2.5 mm, and height 4 mm. Work out the total surface area.
[2 marks]
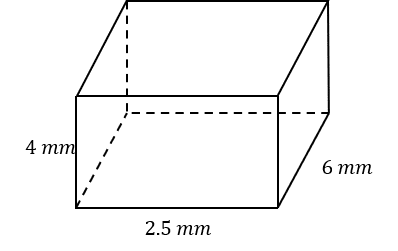
A cuboid has 6 flat, rectangular faces, and we will need the areas of all of them. Specifically, there are 3 pairs of faces since the front and back faces are the same, the top and bottom faces are the same, and the left and right faces are the same.
Firstly, the front face is a rectangle with height 4mm and width 2.5mm, so it has area
4\times2.5=10\text{ mm}^2
Therefore, the back face also has area 10\text{ mm}^2.
The face on the right has length 6mm and height 4mm, so it has area
6\times4=24\text{ mm}^2
Therefore, the left face also has area 24\text{ mm}^2
The face on the top has length 6mm and width 2.5mm, so it has area
6\times2.5=15\text{ mm}^2
Therefore, the bottom face also has area 15\text{ mm}^2.
Thus, adding all these values together, we get the total surface area to be
10+10+24+24+15+15=98\text{ mm}^2
Question 2: Below is a cone with surface area 120\text{ cm}^2. Its base has radius 3 cm. Work out the slant height of the cone to 1 dp.
The formula for the curved surface area of a cone is \pi rl, where r is the radius of the base and l is the slant height. Give your answer to 1 decimal place.
[2 marks]
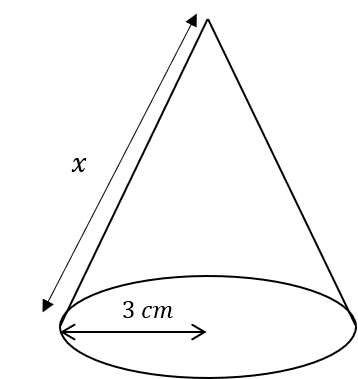
We know the whole surface area is 120\text{cm}^2 and we also know the radius. To work out the slant height, we need to first work out what the curved surface area is. In other words, we need to subtract the surface area of the base of the cone (since that’s the only other face) from 120 to get the curved surface area. The base is a circle, so its area is:
\pi \times 3^2=9\pi\text{ cm}^2
Subtracting this from the total we have
120-9\pi=91.725...
This is written as a decimal to give an idea of how big it is, but when you put it into your calculator you should either use the ANS key to store the value, or you should directly type in 120-9\pi. If you don’t, it could affect your final answer.
Now, this must the area of the curved face, and the formula for the area of the curved face is given to us: \pi rl = 3\pi l (since we know r=3). So, setting this formula equal to the value we worked out, we get
3\pi l=120-9\pi
Then, to find the slant height, we will divide both sides by 3\pi to get
\dfrac{120-9\pi}{3\pi}=9.7\text{ cm (1dp)}.
Question 3: Josh is painting a very large spherical sculpture. The sculpture has radius 8.5 m. He is using a special type of paint that costs £9.60 per pot, and each pot covers exactly 10 m^2. How much will he have to spend in order to paint the whole sphere?
The formula for the surface area of a sphere is 4\pi r^2 where r is the radius.
[3 marks]
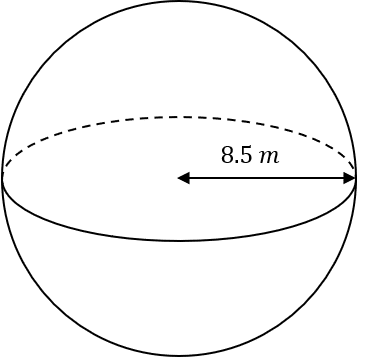
We need to firstly work out the surface area of the sphere. So, with r=8.5, we get
\text{surface area }=4\times\pi\times(8.5)^2=907.920...\text{ m}^2
Now, since each pot covers ten square metres, we must divide this value by 10 to see how many pots he will require:
907.920... \div 10=90.720...
Since he can’t buy exactly 90.720… pots, he will have to buy 91 to cover the whole sphere. Therefore, the cost of all his paint will be
91\times 9.60=\pounds873.60
That’s a lot of paint.
Question 4: The diagram below shows a triangular prism ABCDEF. CB=6 cm and BE=11 cm.
The vertical height of the prism = 8 cm. Calculate the surface area of the triangular prism. Give your answer to 2 decimal places.
[3 marks]
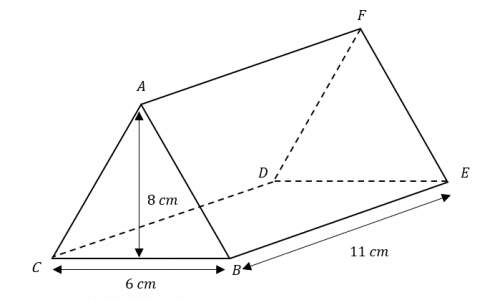
The area of the two triangular faces is,
\text{area}=2\times \dfrac{1}{2}\times 6\times 8 = 48\text{ cm}^2
The area of the rectangular base is,
\text{area}=6\times 11 = 66 \text{ cm}^2
To find the area of the two sides we have to first find the slanted height of the prism:
\text{AB}=\sqrt{8^2+3^2} =\sqrt{73}
Hence, the area of the two sides are:
\text{area}=2\times 11\times \sqrt{73}
Total surface area:
\text{surface area }=48+66+\sqrt{73}= 301.97\text{ cm}^2
Question 5: The diagram shows a square-based pyramid that has a vertical height of 10 cm. Given also that length DC = 12 cm, find the surface area of the square-based pyramid.
[3 marks]
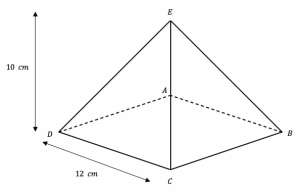
The area of the square base is,
\text{area}=12\times12=144\text{cm}^2
Finding the length of the midpoint of DC to E:
\sqrt{10^2+6^2} = \sqrt{136}
Hence the area of the 4 triangular faces is,
4\times\dfrac{1}{2}\times12\times\sqrt{136}= 279.89\text{cm}^2
Total surface area:
\text{surface area}=279.89+144= 423.89\text{ cm}^2





