Similar Shapes and Enlargements

GCSEKS3Level 4-5Level 6-7AQACambridge iGCSEEdexcelEdexcel iGCSEOCRWJEC

Similar Shapes and Enlargements Revision

Similar Shapes

Two shapes are said to be mathematically similar if all of the angles in the shapes are equal, but the shapes are not necessarily the same size.

We relate two similar shapes of different sizes with a scale factor.

Make sure you are happy with the following topics before continuing.

– 2D Shapes and Quadrilaterals

– Basic ratio questions

Finding the Scale Factor

The first step for any similar shape question will often be to find the scale factor.

To do this we need to find two corresponding dimensions. For the example below we will use lengths.

(Surface area and volume can also be used, these are HIGHER ONLY)

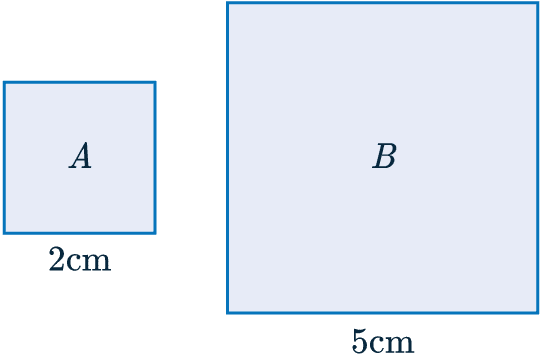
Example: $A$ and $B$ are mathematically similar shapes.

Find the scale factor from $A$ to $B$ .

First we need to find two corresponding lengths.

We can see that the base of $A=2$ cm and $B=5$ cm.

To calculate the scale factor we divide the larger by the smaller:

$5 \div 2 = 2.5$

Scale factor = $2.5$

Note: Once the scale factor has been found it can be used to find missing lengths.

Similar Shapes: Area and Volume

We can extend the idea of similarity further to include areas and volumes.

You can use the following table to find the corresponding measure of a mathematically similar shape.

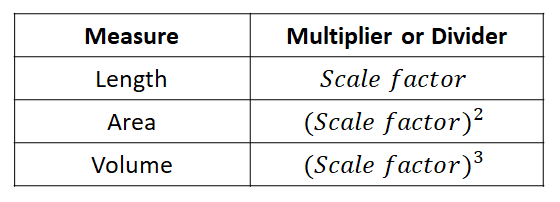
similar shapes area and volume

You multiply when finding the measure of a larger shape and divide for a smaller shape. See the examples below.

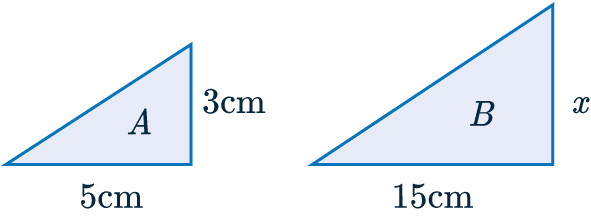
Example 1: Similar Shapes

Shapes $A$ and $B$ are mathematically similar. Find the missing side-length marked $x$ .

similar shapes triangles

[2 marks]

Firstly, we must calculate the scale factor.

To do this we divide the base of shape B by the equivalent side length on shape A

$\textcolor{blue}{\text{Scale factor }}=15\div5=\textcolor{blue}{3}$

Now we have that the scale factor is $\textcolor{blue}{3}$ , all we need to do to find $x$ is multiply $\textcolor{blue}{3}$ by the length of the corresponding side on the smaller shape. So we get

$x=\textcolor{blue}{3}\times3=9$

$x=9$ cm

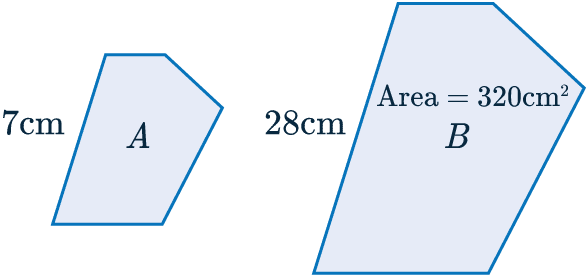
Example 2: Similar Shapes Area

$A$ and $B$ are mathematically similar shapes.

Work out the area of shape $A$ .

similar shapes area

[3 marks]

Firstly, we will determine the scale factor that relates the side-lengths, dividing the larger by the smaller

$SF=28\div7=\textcolor{red}{4}$ .

Now, if the scale factor for the side-lengths is $\textcolor{red}{4}$ , then that means that the scale factor for the areas is:

$SF_A=\textcolor{red}{4}^2=\textcolor{blue}{16}$

Therefore, to find the area of the smaller shape, we need to divide the area of the bigger shape by the area scale factor: $16$ . Doing so, we get

$\text{Area of A }=320\div\textcolor{blue}{16}=20 \text{ cm}^2$

Example 3: Similar Shapes Volume

$A$ and $B$ are mathematically similar shapes.

The volume of shape $A = 600\text{ cm}^3$

Work out the volume of shape $B$ .

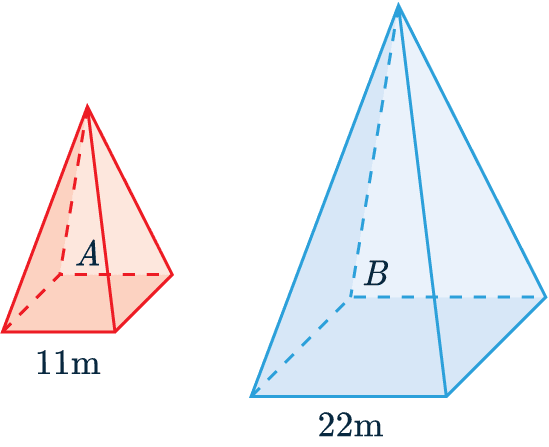
similar shapes volume pyramid

[3 marks]

Firstly, we will determine the scale factor that relates the side-lengths, dividing the larger by the smaller

$SF=22\div11=\textcolor{red}{2}$ .

Now, if the scale factor for the side-lengths is $\textcolor{red}{4}$ , then that means the scale factor for the volumes is:

$SF_V=\textcolor{red}{2}^3=\textcolor{blue}{8}$

We know the volume of shape $A$ and the Volume scale factor $= \textcolor{blue}{8}$ .

So we need to multiply the volume of $A$ by $SF_V$ ,

Volume of $B = 600 \times \textcolor{blue}{8} = 4800\text{ cm}^3$

Similar Shapes and Enlargements Example Questions

Question 1: Shapes $P$ and $Q$ are mathematically similar. The area of shape $P$ is $6\text{cm}^2$ .

a) Calculate the size of missing side-length $x$ .

b) (HIGHER ONLY) Calculate the area of shape $Q$ .

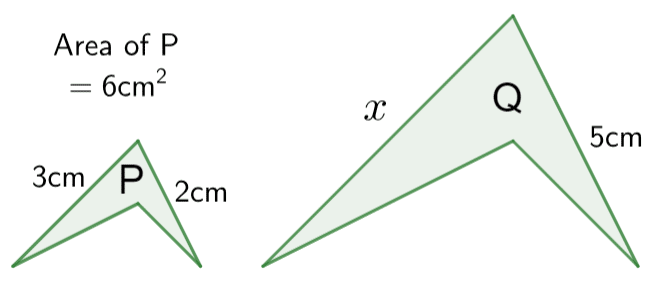
similar shapes example 1

[3 marks]

a) To work out the scale factor, $SF$ , we need to divide the given side-length on the bigger shape by the corresponding side of the smaller shape. Doing so, we get

$SF=5\div2=2.5$

Then, to find $x$ , we must multiply this value by the corresponding side-length of the smaller shape. So, we get

$x=2.5\times3=7.5\text{ cm}$

b) To find the scale factor for the areas, $SF_A$ , we must square the known scale factor:

$SF_A=2.5^2=6.25$

Now, to get the area of the bigger shape, we must multiply the area of the smaller one by this scale factor. Doing so, we get

$\text{Area of Q}=6\times6.25=37.5\text{ cm}^2$

Save your answers with

Gold Standard Education

Question 2: The two triangles, $ABC$ and $DEF$ shown below are mathematically similar.

a) What is the scale factor that transforms $ABC$ to $DEF$ ?

b) Calculate the length $AC$ .

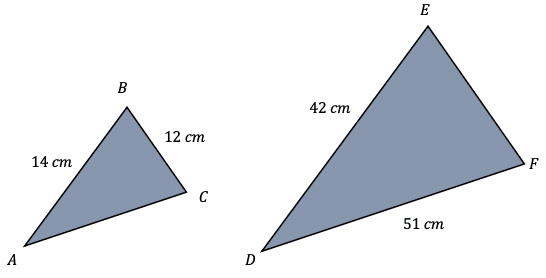
similar shapes example 2 triangles

[3 marks]

a) To work out the scale factor, $SF$ , we need to divide the given side-length on the bigger shape by the corresponding side of the smaller shape. Doing so, we get

$SF=42\div14=3$

b) Now we have the scale factor, we can apply it to the corresponding length to AC which is DF. Hence, we find that,

$\text{AC} =51\div3=17 \text{cm}$

Save your answers with

Gold Standard Education

Question 3: Triangles $BCA$ and $BED$ are mathematically similar. Given that $BC=4.4$ cm, $BA=3$ cm, $AD=3$ cm, and $AC=5$ cm.

a) Find the scale factor that transforms $ABC$ to $BDE$ .

b) Calculate the length of $BE$ .

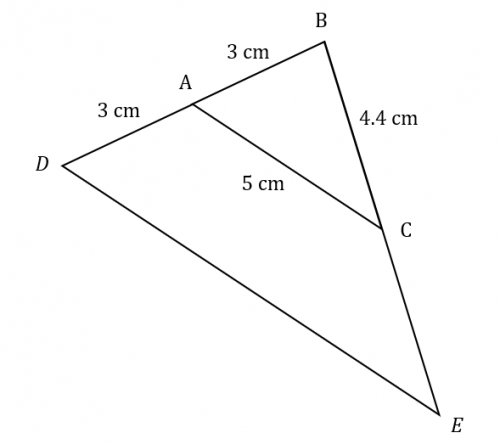
similar shapes example 3 triangles

[3 marks]

a) To work out the scale factor, $SF$ , we need to divide the given side-length on the bigger shape by the corresponding side of the smaller shape. Doing so, we get,

$SF=6\div3=2$

b) Now we have the scale factor, we can apply it to the corresponding length to BE which is BC. Hence, we find that,

$\text{AC} =4.4\times2=8.8 \text{cm}$

Save your answers with

Gold Standard Education

Question 4: Work out the ratio of the surface area of the two mathematically similar spheres shown below. Give your answer in its simplest form.

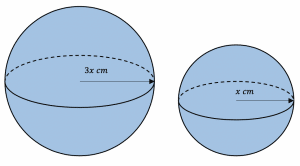
[3 marks]

If the scale factor is 3 then the surface area is,

$3^2=9$

9 times bigger as shown by the calculation above. So we get

$\text{SA of larger sphere : SA of smaller sphere} = 9 : 1$

Save your answers with

Gold Standard Education

Question 5: The diagram shows two mathematically similar rectangles, $ABEF$ and $ACDF$ . Find the scale factor, giving your answer in surd form.

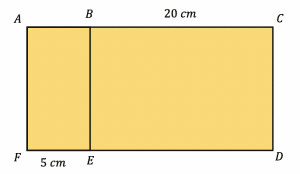
similar shapes example 5 rectangles

[4 marks]

To work out the scale factor, $SF$ , we need to divide the given side-length on the bigger shape by the corresponding side of the smaller shape. However, in this case we are not given two corresponding sides. Instead we can set an unknown length BE, as $x$ and form the equation,

$\dfrac{x}{5}=\dfrac{25}{x}$

Rearranging to find,

$x^2=125$

$x= \sqrt{125}$

Now we have two corresponding sides that we can use to find the scale factor,

$SF=\dfrac{25}{\sqrt{125}}$

Save your answers with

Gold Standard Education