Ratios
Ratios Revision
Ratios
Ratios are a way of expressing one thing compared to another, if x:y is in the ratio of 1:2 this means y is twice the size of x. There are 8 skills involving ratios you need to learn.
Make sure you are happy with the following before continuing:
Skill 1: Writing Ratios as Fractions
Ratios can be written as a fraction in a couple of ways.
Example: Red to blue counters are in a bag in the ratio (\textcolor{red}{3} :\textcolor{blue}{2} ).
There are \dfrac{\textcolor{red}{3}}{\textcolor{blue}{2}} as many red counters as blue counters.
There are \dfrac{\textcolor{blue}{2}}{\textcolor{red}{3}} as many blue counters as red counters.
Alternatively, we can write either part as a fraction of the total i.e. \dfrac{\textcolor{blue}{2}}{\textcolor{black}{5}} of the counters in the bag are blue.
Skill 2: Simplifying
To simplify a ratio we divide all parts of the ratio by a common factor.
Example: Write the following ratio in its simplest form, \textcolor{red}{15}:\textcolor{blue}{30}:\textcolor{limegreen}{24}
All we do is divide each number by the highest common factor of all three numbers, which is 3.
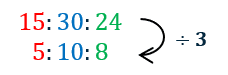
We can not simplify this any more, therefore the ratio is in its simplest form.
Skill 3: Scaling Ratios
To scale a ratio we multiply by a common factor.
Example: Meringue is made by mixing cups of egg whites and cups of sugar in the ratio \textcolor{limegreen}{3}:\textcolor{blue}{7}. How many cups of sugar are needed if \textcolor{limegreen}{12} cups of egg whites are used in the mixture? We know that \textcolor{limegreen}{12} = \textcolor{limegreen}{3} \times \textcolor{black}{4}, so we need to multiply the ratio by \textcolor{black}{4}
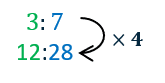
So when \textcolor{limegreen}{12} egg whites are used, \textcolor{blue}{28} cups of sugar are needed.
Skill 4: Part to Whole Ratios
Sometimes you may see ratios x:y where y includes x. These are part : whole ratios.
Example: Adam has some apples and oranges in his bag. The ratio of oranges to fruit in his bag is \textcolor{orange}{2}:\textcolor{blue}{7}.
a) Finding the fraction of a whole – What fraction of Adam’s fruit are oranges?
For every \textcolor{blue}{7} pieces of fruit, \textcolor{orange}2 of these are oranges.
\large{\frac{\text{part}}{\text{whole}} = \frac{2}{7}}
b) Finding the ratio of a part – What is the ratio of oranges to apples?
\textcolor{orange}{2} out of every \textcolor{blue}{7} pieces of fruit are oranges, so \textcolor{blue}{7} - \textcolor{orange}{2} = \textcolor{limegreen}{5} out of every \textcolor{blue}{7} pieces of fruit are apples. For every \textcolor{orange}{2} oranges there are \textcolor{limegreen}{5} apples
\text{\textcolor{Orange}{oranges} : \textcolor{limegreen}{apples}} = \textcolor{orange}{2} : \textcolor{limegreen}{5}
c) Finding the missing amount – Adam has \textcolor{orange}{4} oranges, how many apples does he have?
We need to scale up the ratio \textcolor{orange}{2}:\textcolor{limegreen}{5}, so that the left is equal to \textcolor{orange}{4}. So we multiply the ratio by \textcolor{black}{2}.
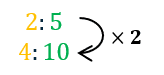
So, Adam has \textcolor{limegreen}{10} apples.
Skill 5: Dividing Amounts into Ratio
Being able to split a total amount into a ratio is a key skill needed.
Example: Aaron, Kim and Paul split \textcolor{purple}{£6000} in the ratio of \textcolor{red}{3}:\textcolor{limegreen}{4}:\textcolor{blue}{5}. How much money does Aaron receive?
Step 1: Find the total number of parts in the ratio:
\textcolor{red}{3}+\textcolor{limegreen}{4}+\textcolor{blue}{5} = \textcolor{black}{12} parts.
Step 2: Divide the total amount by the total number of parts in ratio, this finds the value of 1 part.
\textcolor{purple}{£6000} \div \textcolor{black}{12} = \textcolor{orange}{£500} = \, 1 part
Step 3: Multiply the value of one part by the number of parts Aaron has:
\textcolor{orange}{£500} \times \textcolor{red}{3} = £1500
So Aaron gets £1500.
Skill 6: Difference Between Parts of a Ratio
You may sometimes be given the difference between two parts of the ratio, instead of the total amount.
Example: Josh, James and John share sweets in the ratio \textcolor{orange}{1}:\textcolor{blue}{2}:\textcolor{red}{4}. Josh has \textcolor{limegreen}{9} sweets less than John. How many sweets does James have?
Step 1: Firstly, work out how many parts of the ratio \textcolor{limegreen}{9} sweets makes up:
\textcolor{limegreen}{9} \, \text{sweets} = \text{John's sweets} - \text{Josh's sweets} = \textcolor{red}{4} \, \text{parts} - \textcolor{orange}{1} \, \text{part} = 3 \, \text{parts}.
Step 2: Then divide to find 1 part:
\textcolor{limegreen}{9} \, \text{sweets} \div 3 = \textcolor{purple}{3} \, \text{sweets}
\textcolor{purple}{3} \text{ sweets } = 1 \text{ part }
Step 3: Multiply by the number of parts James has to find how many sweets he has:
\text{James' sweets} = \textcolor{blue}{2} \, \text{parts} = \textcolor{blue}{2} \times \textcolor{purple}{3} \, \text{sweets} = \bf{6 \, \text{sweets}}
Skill 7: Changing Ratios
You need to be prepared for questions where the ratio changes.
Example: Billy and Claire share marbles in the ratio \textcolor{blue}{5}:\textcolor{limegreen}{3}. Billy gives \textcolor{orange}{4} marbles to Claire and the ratio is now 1:1. How many sweets did each have initially?
Step 1: At first, Billy had \textcolor{blue}{5}x marbles and Claire had \textcolor{limegreen}{3}x marbles.
Step 2: Billy gives \textcolor{orange}{4} marbles to Claire. Now, Billy has \textcolor{blue}{5}x-\textcolor{orange}{4} marbles and Claire has \textcolor{limegreen}{3}x+\textcolor{orange}{4}.
Step 3: The ratio \textcolor{blue}{5}x-\textcolor{orange}{4} : \textcolor{limegreen}{3}x+\textcolor{orange}{4} is 1:1.
\dfrac{\textcolor{blue}{5}x-\textcolor{orange}{4}}{\textcolor{limegreen}{3}x+\textcolor{orange}{4}} = \dfrac{1}{1}
Rearranging and solving for x,
\begin{aligned} (\textcolor{blue}{5}x-\textcolor{orange}{4})& = (\textcolor{limegreen}{3}x+\textcolor{orange}{4}) \\ \textcolor{blue}{5}x &= \textcolor{limegreen}{3}x+\textcolor{orange}{8} \\ 2x &= \textcolor{orange}{8} \\ x &= 4 \end{aligned}
Initially, Billy had \textcolor{blue}{5x = 20} marbles and Claire had \textcolor{limegreen}{3x = 12}.
Skill 8: Reducing Ratios to the form 1 : n
To reduce a ratio to the form 1:n or n:1, all you have to do is divide the whole ratio by the smallest number.
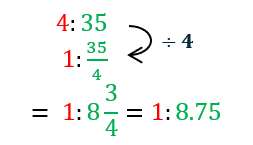
Example 1: Scaling and Simplifying Decimal Ratios
Write the following ratio in its whole number simplest form.
[2 marks]
First, we need to multiply all parts of the ratio until there are only whole numbers left before simplifying.
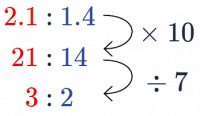
Example 2: Simplifying Ratios that have Different Units
Change the following ratio into the same unit ratio in its simplest form.
[2 marks]
If ratios have different units, we need to convert one of the units to the other, then simplify the ratio to its simplest form.
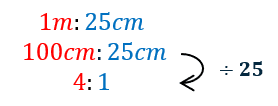
Ratios Example Questions
Question 1: In a school, the ratio of the number of students with blonde hair to the number of students with brown hair is 4:5.
a) What fraction of students have blonde hair?
b) If there are 450 students in the school, how many of them have brown hair?
[3 marks]
a) In order to work out the fraction of students that have blonde hair, we need to add up the ratio parts. The sum of the ratio is 4 + 5 = 9. This means that we are dealing with 9ths. Since the ratio share for blond students is 4, this means that the fraction of blonde students is \dfrac{4}{9}
b) We know from the previous question that \dfrac{4}{9} of the students have blonde hair. Therefore, the fraction of students with brown hair is \dfrac{5}{9}. If there is a total of 450 students in the school, we need to work out what \dfrac{5}{9} of 450 is:
\dfrac{5}{9} \times 450 = 250 students.
Question 2: Divide 35 in the ratio 2 : 5.
[2 marks]
In total, there are 7 parts to this ratio (2 + 5 = 7). If 7 shares have a value of 35, then 1 share has a value of 5 (35 \div 7 = 5).
Since 1 share has a value of 5, then 2 shares will have a value of 10 (2 \times 5 = 10).
Since 1 share has a value of 5, then 5 shares will have a value of 25 (5 \times 5 = 25).
Question 3: Lucy is tiling her bathroom. She buys white and blue tiles in the ratio of 13 : 2. Blue tiles cost £2.80 whilst white tiles cost £2.35. If she buys 16 blue tiles, how much does Lucy spend on tiles in total?
[3 marks]
To work out the total cost of the tiles Lucy buys, we need to work out how many white tiles she buys. In order to work out the number of white tiles, we need to work out the total number of tiles she buys.
The ratio is 2 parts blue to 13 parts white. If Lucy buys 16 blue tiles, this is 8 times more than the figure for blue tiles in the ratio (16\div2=8).
If the number of blue tiles she buys is 8 times more than the blue tiles figure given in the ratio, then the number of white tiles she buys must also be 8 times more than the white tiles figure in the ratio. Therefore, the number of white tiles she buys is:
13\times8 = 104 white tiles
Now that we know how many tiles of each colour she has bought, we can calculate the total cost of the tiles.
The cost of 16 blue tiles is:
16\times2.80 = \pounds44.80
The cost of 104 white tiles is:
104\times2.35 =\pounds244.40
Therefore, Lucy’s total spend on tiles is:
44.80+244.40=\pounds289.20
Question 4: Steve receives £200 each month from his parents as an allowance. 20 \% of this amount is spent on his football magazine subscription, and the rest he spends on football stickers, sweets and fizzy drinks in the ratio of 5 : 2 : 1. How much does Steve spend on football stickers?
[2 marks]
The first thing we need to do is to deduct the 20 \% spent on the magazine subscription so that we can work out how much of his allowance Steve has left over. 20 \% of £200 can be calculated as follows:
0.2 \times \pounds 200 = \pounds 40
You may prefer to calculate the 20% in your head:
10 \% of £200 is £20, so 20 \% is
2 \times \pounds 20 = \pounds 40
Then deduct this from £200:
\pounds200 - \pounds40 = \pounds160
Steve therefore has £160 pounds remaining which he spends on sweets, football stickers and fizzy drinks in the ratio of 5 : 2 : 1.
By adding up the ratio, we know that we are dealing with eighths. (We know we are dealing in eighths because 5 + 2 + 1 = 8). We know from the ratio that the share he spends on football stickers is 5, meaning that Steve spends \frac{5}{8} of the remaining allowance on football stickers.
The actual amount that Steve spends on football stickers can be calculated as follows:
\dfrac{5}{8} \times \pounds160 = \pounds100
Question 5: Alieke, Jon, and Kate tracked the number of books they read last year. Jon read twice as many books as Kate, but Alieke read 4 times as many books as Jon.
a) Write down a ratio of the number of books read by Alieke to the number of books read by Jon to the number of books read by Kate.
b) Alieke read 63 more books than Kate last year. Work out how many books Alieke, Jon, and Kate read in total last year.
[4 marks]
a) We are told that Jon reads twice as many books as Kate. As a ratio, this can be written as 2 : 1.
We are also told that Alieke reads 4 times as many books as Jon. As a ratio, this can be written as 4 : 1.
The issue we have now is that in the Jon : Kate ratio, Jon’s share is 2, while in the Alieke : Jon ratio, Jon’s share is 1. By doubling the 4 : 1 ratio for Aleike : Jon to 8 : 2, Jon’s share is now the same in both ratios.
This means that we can express this is a 3-way ratio as follows:
\text{Alieke : Jon : Kate }= 8 : 2 : 1
b) We are told that Alieke read 63 more books than Kate last year, and we know from the previous part of the question that the Alieke : Kate reading ratio is 8 : 1. In this ratio, the share is 8 parts to 1 part, so we can conclude that the difference between the ratio share is 7 parts (8 - 1 = 7).
If the difference in the ratio share is 7 parts, and the difference in the number of books read is 63, then we can work out the number of books read that 1 share of the ratio represents:
63 \div 7 = 9\text{ books}
If one share of the ratio represents 7 books read, we can now work out how many books were read in total by the three people. By adding up the ratio, we know that the total number of shares is 11 (8 + 2 + 1 = 11), so the total number of books read can be calculated as follows:
11 \times 9\text{ books} = 99\text{ books}
Ratios Worksheet and Example Questions
(NEW) Ratios (Foundation) Exam Style Questions - MME
Level 4-5GCSENewOfficial MME(NEW) Ratios (Higher) Exam Style Questions - MME
Level 6-7GCSENewOfficial MMERatios Drill Questions
Ratio Foundation
Level 4-5GCSERatio and Percentages
Level 4-5GCSE
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now




