Revise
Gradients of Straight Line Graphs
Gradients of Straight Line Graphs Revision
Gradients of Straight Line Graphs
Equations featuring x and y (and no x^3 or y^2 etc.) are straight lines.
The gradient of a line is a measure of how steep it is. If the gradient is small, the slope of the line will be very gradual, but if the gradient is big, the line will be quite steep. You are required to know how to calculate the gradient from two possible circumstances:
- You are given the line drawn on a graph.
- You are given two coordinates and told that a line passes through both of them.
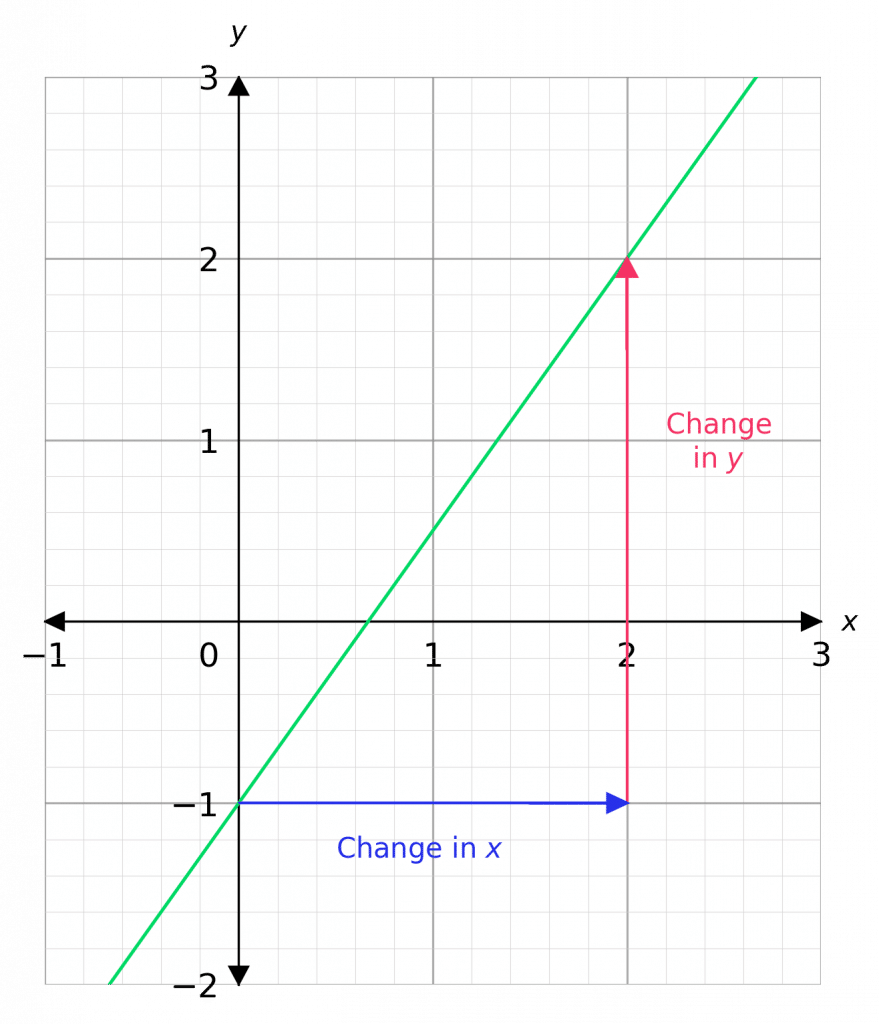
Finding the Gradient of a Straight Line
Example: Find the gradient of the line shown:
In general, if we have two coordinates (\textcolor{blue}{x_1}, \textcolor{red} {y_1}) and (\textcolor{blue}{x_2}, \textcolor{red}{y_2}) then the gradient of the line that passes through them is,
\begin{aligned} \text{Gradient } &= \dfrac{\text{change in }\textcolor{red}{y}}{\text{change in }\textcolor{blue}{x}} = \dfrac{\textcolor{red}{y_2 - y_1}}{\textcolor{blue}{x_2 - x_1}} \\ \\ & = \dfrac{2 - (-1)}{2 - 0} = \dfrac{3}{2} \end{aligned}
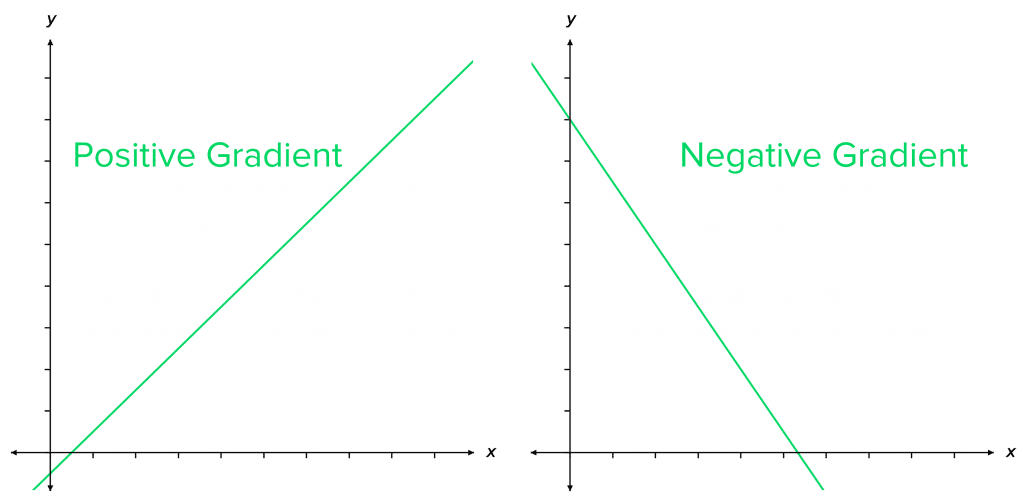
Positive vs Negative Gradients
- Positive gradient: \textcolor{red}{y} value increases as the \textcolor{blue}{x} value increases.
- Negative gradient: \textcolor{red}{y} value decreases as the \textcolor{blue}{x} value increases.
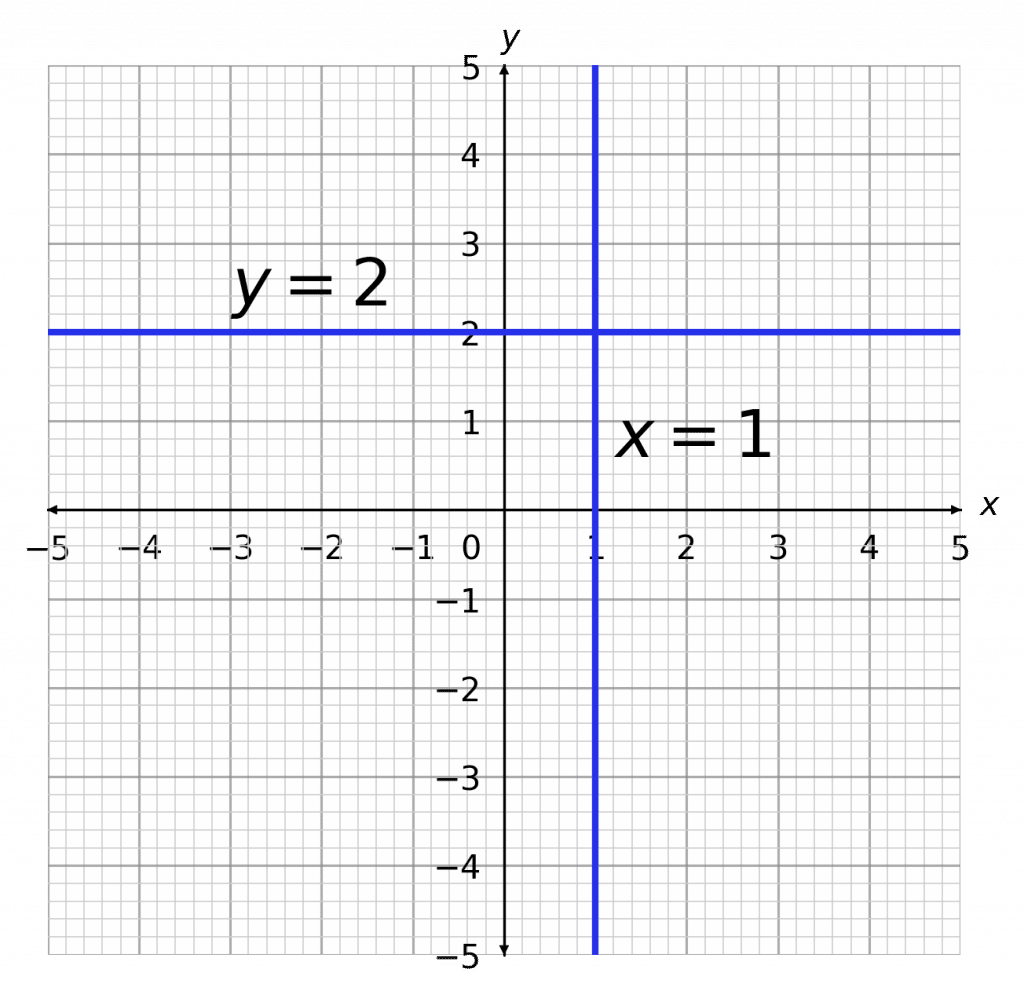
Horizontal and Vertical Lines
Horizontal lines: y = a (constant y value)
Vertical lines: x=a (constant x value)
Example: Draw the graphs of x=1 and y=2.
When drawing such lines, find the coordinate on the correct axis, i.e. for x=1, find (1,0) and draw a straight line perpendicular to that axis which results in a vertical line.
Similarly for y=2, find (0,2) and draw a straight line perpendicular to that axis, which in this case is a horizontal line.
Example: Find the Gradient of a Line Through Two Points
Work out the gradient of the straight line that passes through the points (2, 3) and (-10, 6).
Step 1: pick one of the points and subtract its x and y coordinates from the other point’s x and y coordinates respectively.
\text{change in } y = (y_1 - y_2) = (6-3) = 3
\text{change in } x = (x_1 - x_2) = (-10-2) = -12
Step 2: Substitute in to the formula,
\text{gradient } = \dfrac{\text{change in } y}{\text{change in } x} = \dfrac{3}{-12} = -\dfrac{1}{4}
Gradients of Straight Line Graphs Example Questions
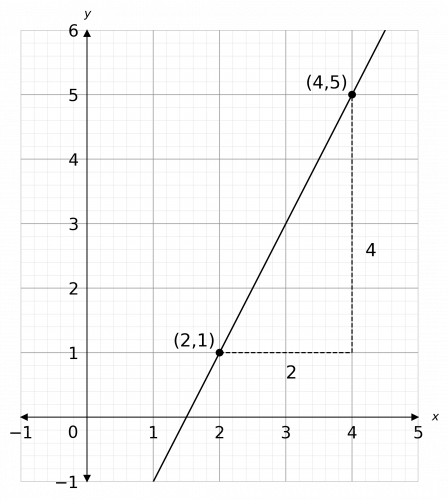
Question 1: Calculate the gradient of the line drawn below.
[2 marks]
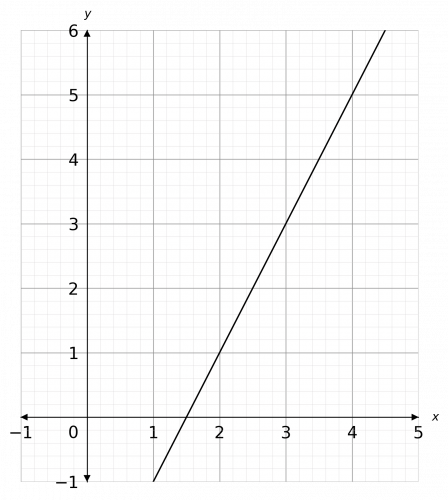
To do this, you want to pick 2 points on the graph that the line passes through. It’s best, if you can, to pick two points where the coordinates are easy to read off. Here, we picked (2, 1) and (4, 5), as seen on the graph.
Once you’ve done this, draw the right-angled triangle as pictured with dotted lines. Then, the change in x is the width of the base of that triangle, whilst the change in y is the height.
Therefore, we get
\text{gradient } = \dfrac{\text{change in }y}{\text{change in }x}= \dfrac{4}{2} = 2
Question 2: Calculate the gradient of the line drawn below.
[2 marks]
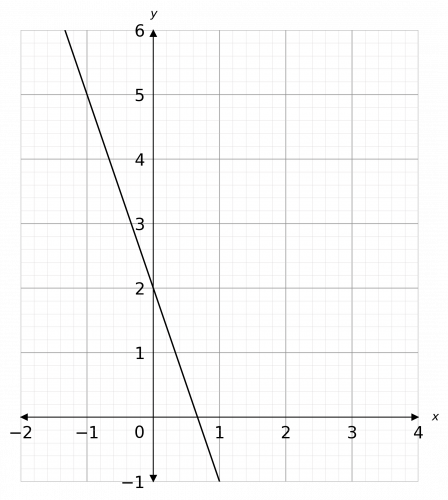
We must find two points that the line passes through and draw a right-angled triangle underneath, so we can identify the change in x to be the base and the change in y to be the height. This looks like
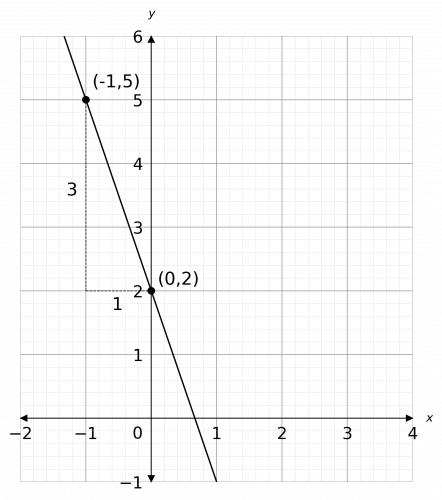
Now, given that this is a downwards slope, it must have a negative gradient. So, we get
\text{gradient } = -\dfrac{3}{1} = -3
Note: you could’ve used a different triangle at different points on the line – this is fine, as long as you got the correct answer of - 3.
Question 3: Find the gradient of the line that passes through (-8, -1) and (2, -6).
[2 marks]
To find the gradient, we’ll subtract the values of second coordinate from those of the first, and divide the difference in the y values by the difference in the x values:
\text{gradient } = \dfrac{-1 - (-6)}{-8 - 2} = \dfrac{5}{-10} = -\dfrac{1}{2}
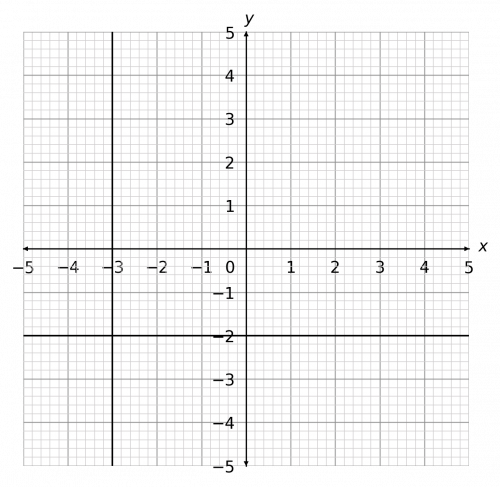
Question 4: Draw the lines y=-2 and x=-3 on a single graph.
[2 marks]
When drawing lines of the form x=a or y=b, find the coordinate on the correct axis and draw a straight line perpendicular to that axis.
For y=-2, find (0,-2) and draw a straight line perpendicular to that axis which is a horizontal line.
For x=-3, find (-3,0) and draw a straight line perpendicular to that axis which is a vertical line.
Gradients of Straight Line Graphs Worksheet and Example Questions
(NEW) Gradients of Straight Line Graphs Exam Style Questions - MME
Level 1-3NewOfficial MMEGradients of Straight Line Graphs Drill Questions
Straight Line and Gradients - Drill Questions
Level 4-5GCSE
Gradients of Straight Line Graphs - Drill Questions
Level 1-3GCSE
Straight Line Graphs - Drill Questions
Level 1-3GCSE
Straight Line Graphs 2 - Drill Questions
Level 1-3GCSE
Graph Exam Questions (harder)
Level 6-7GCSE
