GCSE Maths Equations

GCSELevel 1-3Level 6-7AQAEdexcelOCRWJEC

GCSE Maths Equations Revision

GCSE Maths Formula Sheet

The GCSE maths formula sheet Z-card includes the formulae you will need to learn for your GCSE maths exam. Whether you are doing AQA, Edexcel or OCR, the following list of maths equations are relevant to you.

Click here to see our Equations To Memorise Z-Card

Download free B&W free PDF Version

Algebra

Higher Only

The quadratic equation:	$\textcolor{blue}{a}x^2+\textcolor{red}{b}x+\textcolor{Orange}{c}=0$
Its solutions are found using the quadratic formula:	$x=\dfrac{-\textcolor{red}{b}\pm\sqrt{\textcolor{red}{b}^2-4\textcolor{blue}{a}\textcolor{Orange}{c}}}{2\textcolor{blue}{a}}$

Direct proportionality: ( $y$ is proportional to $x$ , $x^2$ )	$y \propto x \rightarrow y = \textcolor{limegreen}{k}x$ $y \propto x^2 \rightarrow y = \textcolor{limegreen}{k}x^2$
Inverse proportionality: ( $y$ is inversely proportional to $x$ , $x^2$ )	$y \propto \dfrac{1}{x} \rightarrow y = \dfrac{\textcolor{limegreen}{k}}{x}$ $y \propto \dfrac{1}{x^2} \rightarrow y = \dfrac{\textcolor{limegreen}{k}}{x^2}$

Compound measures

$\text{Speed (s)} = \dfrac{\text{distance (d)}}{\text{time (t)}}$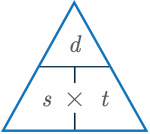
$\text{Density (d)} = \dfrac{\text{mass (m)}}{\text{volume (V)}}$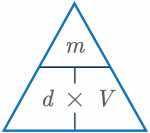
$\text{Pressure (p)} = \dfrac{\text{force (F)}}{\text{area (A)}}$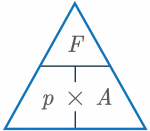

Geometry

Area of a rectangle $=l \times w$
Area of a triangle $=\dfrac{1}{2} b \times h$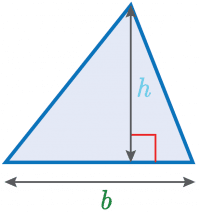
Area of a Parallelogram $= b \times h$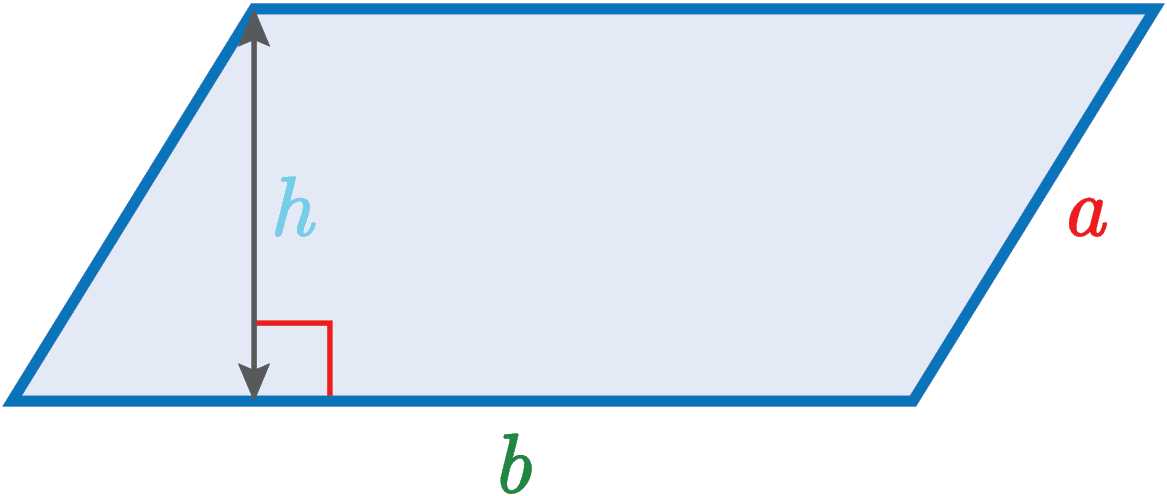
Area of a Trapezium $= \dfrac{1}{2}(a + b) \times h$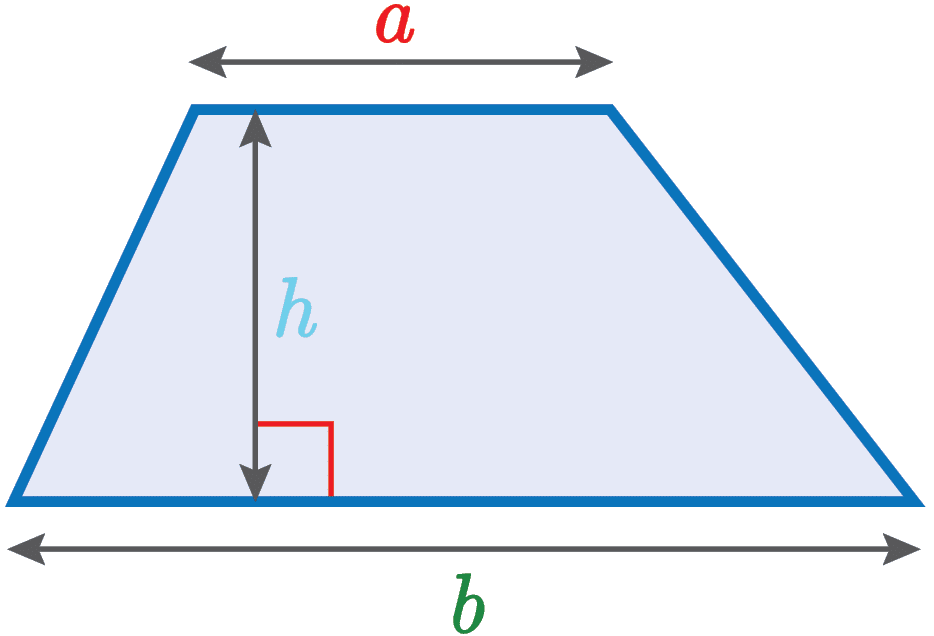
Sum of interior angles for a regular polygon $= (\text{number of sides } – \, 2) × 180$
Interior angle of a regular polygon $=\dfrac{(\text{number of sides } – \, 2) \times 180}{\text{number of sides}}$
Exterior angle of a regular polygon $=\dfrac{360}{\text{number of sides}}$

Circles

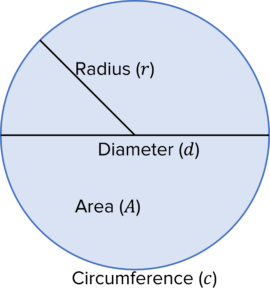
Circumference $=c=2\pi r=\pi d$

Area $=A=\pi r^{2}$

GCSE Maths Equations to memorise

Click here to see our Equations To Memorise Z-Card

Volumes

Higher Only

Volume of a cuboid $=\text{ length }\times\text{ width }\times\text{ height}$
Volume of a prism $=\text{ area of cross section }\times{ \text{length}}$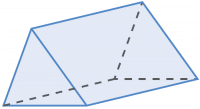
Volume of a cylinder $=\pi r^2 h$
Volume of a pyramid $=\dfrac{1}{3}\times\text{ area of base }\times\text{ vertical height }$
Volume of sphere $=\dfrac{4}{3}\pi r^{3}$ Surface area of sphere $=4\pi r^{2}$
Volume of cone $=\dfrac{1}{3}\pi r^{2}h$ Curved surface area of cone $=\pi rl$ where $l$ is the slant height

Pythagoras and Trigonometry

Higher Only

Pythagoras’ theorem: $a^2 +b^2 = c^2$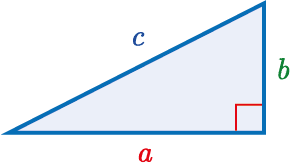
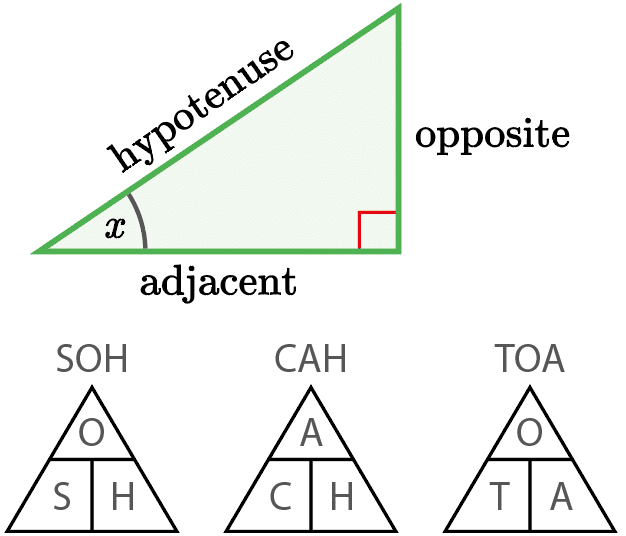
$\sin(x) = \dfrac{\text{opp}}{\text{hyp}}\,\,\,\,$ $\cos(x) = \dfrac{\text{adj}}{\text{hyp}}\,\,\,\,$ $\tan(x) = \dfrac{\text{opp}}{\text{adj}}$
Sine Rule: $\dfrac{\textcolor{red}{a}}{\sin \textcolor{red}{A}}=\dfrac{\textcolor{limegreen}{b}}{\sin \textcolor{limegreen}{B}}=\dfrac{\textcolor{blue}{c}}{\sin \textcolor{blue}{C}}$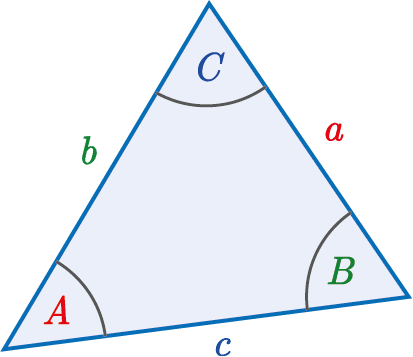
Cosine Rule: $\textcolor{red}{a}^2=\textcolor{limegreen}{b}^2+\textcolor{blue}{c}^2-2\textcolor{limegreen}{b}\textcolor{blue}{c}\cos \textcolor{red}{A}$ or $\cos(\textcolor{red}{A}) = \dfrac{\textcolor{limegreen}{b}^2+\textcolor{blue}{c}^2 - \textcolor{red}{a}^2}{2\textcolor{limegreen}{b}\textcolor{blue}{c}}$
Area of a triangle: $\dfrac{1}{2}ab\sin(C)$

Trigonometry common values: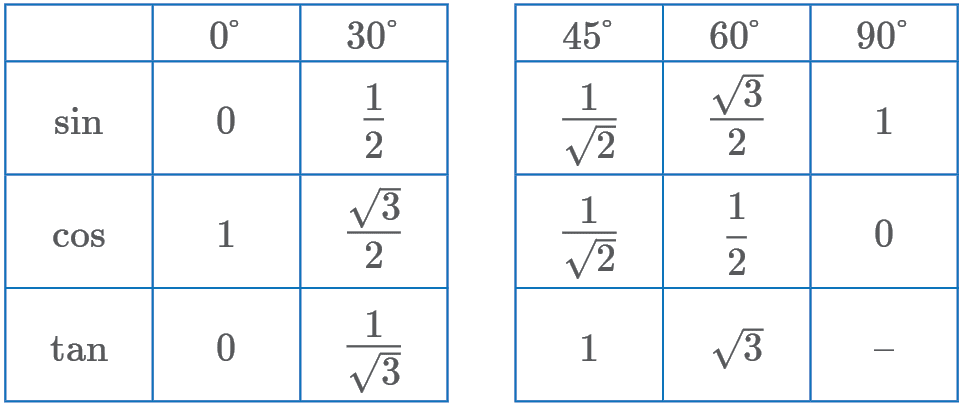

Probability and more

Higher Only

Compound interest:	$\text{New value} = \text{original}\times \bigg(1 +\dfrac{\text{percentage}}{100} \bigg)^{\text{time}}$
Depreciation:	$\text{New value} = \text{original}\times \bigg(1 -\dfrac{\text{percentage}}{100} \bigg)^{\text{time}}$
Percentage of amount:	$\dfrac{\text{percentage}}{100} \times \text{amount}$
Percentage change:	$\text{Percentage Change }= \dfrac{\text{new} - \text{original}}{\text{original}} \times 100$
Histograms:	$\text{Frequency Density }= \dfrac{\text{frequency}}{\text{class width}}$
Probability:	$\begin{aligned}P(A\text{ or }B)&=P(A)+P(B)-P(A\text{ and }B)\\P(A\text{ and }B)&=P(A\text{ given }B)P(B)\end{aligned}$