Relative Formula Mass
Relative Formula Mass Revision
Relative Formula Mass
Relative formula mass, (also called relative molecular mass or RMM and given the symbol Mr) is a way of measuring the mass of a molecule in terms of the relative atomic masses of its constituent atoms. Relative formula mass is defined as the mass of a compound relative to \frac{1}{12}^\text{th} the mass of an atom of Carbon-12 (which is equal to one). In a balanced reaction, the formula masses of the products and reactants will be equal. However, the actual weights of products may be lower that those of the reactants in cases where one or more products is a gas.
Calculating Relative Formula Mass
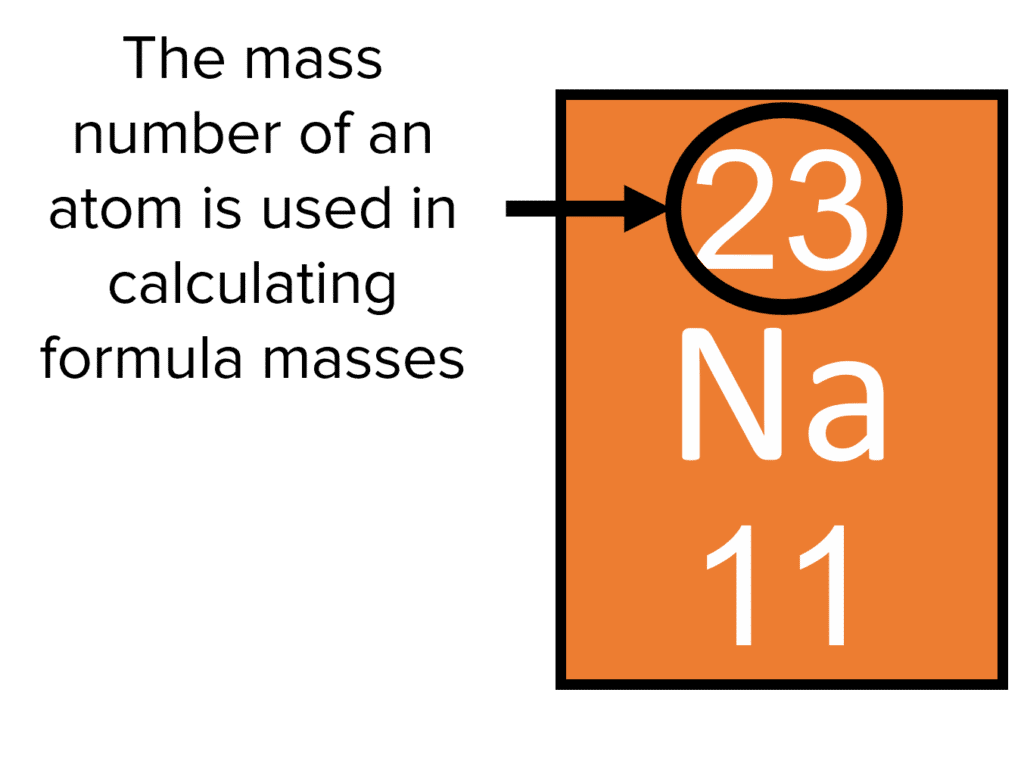
Calculating Relative Formula masses is relatively straightforward. First we look at the formula of a molecule to see which atoms it contains. We then look to the periodic table to find their relative atomic masses (circled in black in the diagram to the right).
Remember, the relative atomic mass is (usually) the larger of the two numbers next to an elements atomic symbol. It is (usually) found in the top of the square an element occupies in the periodic table. Once we have all the atomic masses, we add these up to get the formula mass of the molecule.
Percentage by Mass
By using formula mass and atomic mass, we can work out what percentage of a molecule’s mass a given element makes up. All we have to do is take the formula and atomic masses, and substitute them into the formula below:
\% \text{ Mass of Element } =\frac{\text{Relative Atomic Mass of Element}}{\text{Relative Formula of Compound}} \times 100
Example
The relative formula mass of the molybdenum compound MoOCl4 is 254. Calculate the percent by mass of Molybdenum , (\text{Mo, A}_r 96) in this compound.
\% \text{ Mo } = \text{Atomic Mass Mo} \div \text{Formula Mass}\text{ Molybdenum}\text{ Compound}\\ =\frac{96}{254} \times 100\\ = 0.38 \times 100 = 38 \%
Conservation of Mass
Conservation of mass is an important principle in chemistry, as well as in science more broadly. The principle of the conservation of mass states that:
Mass is neither created nor destroyed in a chemical reaction. The mass of reactant used and the mass of products formed are equal.
In simple terms, what goes in must come out. Atoms can’t simply disappear, as such neither can the mass they account for. Take for example the reaction of 3\text{ g} of sodium with 3\text{ g} of chlorine to form sodium chloride. The mass of the NaCl produced must be 6\text{ g} as no other products are formed, and 6\text{ g} of reactant was used.
Though the total mass of products should always be roughly equal to the mass of reactant used, the masses measured in experiments are not always exactly equal. In some cases, product may be lost in some way (loss of gaseous products is discussed below). In these cases the mass of the products will seem to be as less than the mass of the reactants used.
In other cases, unaccounted for impurities in reactants or reaction vessels may take place in the reaction, creating unexpected products. In these cases the mass of the products will seem to be more than that of the reactant used. It is important to remember that in both cases, the actual mass of reactants (be they intended or accidental) and of the products (gaseous, liquid, or solid) will always be equal once everything has been accounted for.
Balancing Equations
One important consequence of the conservation of mass is that it allows us to write balanced chemical equations for reactions. As mass is conserved in a chemical reaction, so are atoms. The number of reactant atoms used will always be equal to atoms of product produced. If 6 atoms worth of reactant are used, then 6 atoms worth of product must be formed.
Some chemical equations do not require any work to be balanced as they already are. For example, sodium hydroxide reacting with hydrochloric acid:
\text{NaOH + HCl } \rarr \text{ NaCl + H}_2\text{O}
On the left hand side of the equation there is 1 sodium atom, 1 oxygen atom, 1 chlorine atom, and 2 hydrogen atoms. On the left hand side there is 1 sodium atom, 1 oxygen atom, 1 chlorine atom, and 2 hydrogen atoms. As such, we do not need to do anything to balance this equation, the numbers of atoms are equal.
In many cases however, we need to work to make an equation balanced. Take for example the reaction of magnesium hydroxide and hydrochloric acid:
\text{Mg(OH)}_2 \text{ + HCl} \rarr \text{MgCl}_2 \text{ + H}_2 \text{O}
Here, the number of atoms on each side are not equal. On the right hand side we have 1 atom of magnesium, 2 atoms of oxygen, 3 atoms of hydrogen, and 1 atom of chlorine. On the right we have 1 atom of magnesium, 1 atoms of oxygen, 2 atoms of hydrogen, and 2 atom of chlorine.
To get to equal number of atoms on both sides we need to multiply one or more of the molecules in the reaction. We start by multiplying HCl by 2. This means that there are two molecules of HCl reacting with every one of magnesium hydroxide. This gives us 2 chlorine atoms on the right, equaling 2 on the left. Chlorine is now balanced
\text{Mg(OH)}_2 \text{ + } 2 \text{HCl} \rarr \text{MgCl}_2 \text{ + H}_2 \text{O}
However, we now have 4 hydrogen atoms on the left and only 2 on the right. To balance the hydrogen, we need to double the number on the right. To do this, we double the molecules of water formed:
\text{Mg(OH)}_2 \text{ + } 2 \text{HCl} \rarr \text{MgCl}_2 \text{ + } 2 \text{H}_2 \text{O}
This also gives us another oxygen, meaning there are now 2 atoms both left and right. The equation is fully balanced.
Reactions forming gasses
In many reactions, the principle of the conservation of mass seems to be violated. It is not uncommon to find that, after a reaction has taken place, the measured mass of the product formed is not equal to the mass of the reactant used. Though it may seem that this mass has been destroyed, in reality it has simply not been measured. This tends to happen when one or more of the products formed in a reaction is a gas. Take the reaction of bicarbonate of soda and hydrochloric acid.
\text{NaHCO}_{3 (s)}+\text{HCl}_{ (aq)}\rarr\text{NaCl}_{ (s)}+\text{H}_2\text{O}_{ (l)}+\text{CO}_{2 (g)}
This reaction has three products; sodium chloride, water, and carbon dioxide. If this experiment were to be carried out in an open container, the mass of the products would not be equal to that of the reactants. This is not because any mass has been destroyed. Instead, the mass of the products that has been measured is only that of sodium chloride and water.
Because carbon dioxide is a gas, it is able to escape the container, and so is not present when we measure the mass of the products. If we were to calculate the mass of carbon dioxide released, and add this back to the mass of the products, the result should equal the mass of the reactants used.
Example 1: Calculating Relative Formula Mass
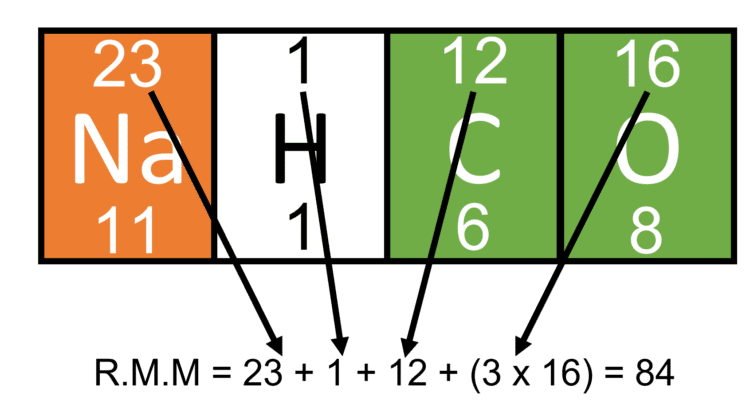
Sodium Hydrogen Carbonate is a common household chemical, otherwise known as bicarbonate of soda. Its molecular formula is NaHCO3. Calculate its relative formula mass (RMM):
[1 mark]
- As we have the molecular formula for this compound, calculating its RMM is straight forward. We have 1 sodium atom, 1 hydrogen atom, 1 carbon atom and 3 oxygen atoms.
- As such, we need to find the atomic mass of a sodium atom, a hydrogen atom, a carbon atom, and an oxygen atom. As there are three oxygen atoms in the formula, we will also need to multiply its atomic mass by 3 when calculating our RMM:
Example 2: Identifying an unknown atom
A student is given a sample of a compound with a relative formula mass (RMM) of 74. The student is told that the compound contains 1 sodium atom, 1 oxygen atom, and 1 other atom. Deduce the identity of the unknown atom:
[2 marks]
- We know that the RMM of the compound is 74
- We also know that there is a sodium atom and an oxygen atom present in the compound
- Using the periodic table, we can work out how much these two atoms together weigh:
\textcolor{#f21cc2}{23} + \textcolor{#10a6f3}{16} = \textcolor{#008d65}{39}
- To find the identity of the unknown atom, we subtract the mass of the sodium and oxygen from the total formula mass to find the relative atomic mass (RAM) of the atom:
74 - 39 = \textcolor{#008d65}{35}
- Now we know the atom has a relative atomic mass of \textcolor{#008d65}{35}. We can use this to find the element on the periodic table who’s RAM is approximately equal to 35. This identifies the unknown atom as chlorine which has an Ar of 35.5.
Relative Formula Mass Example Questions
Question 1: Cis-platin is a common drug used to treat cancers. Its molecular formula is \text{PtCl}_2\left(\text{NH}_3\right)_2. Calculate its relative molecular weight.
[2 marks]
Relative Atomic Masses:
\begin{aligned}\text{Pt} &= 195\\\text{Cl} &= 35\\\text{N} &= 14\\\text{H} &= 1\end{aligned}
\text{RMM} =195 + (2 \times 35) + (2 \times 14) + 6\\= 299
(one mark for the correct calculation, one mark for the correct relative formula mass)
Question 2: Sulfuric acid \left(\text{H}_2\text{SO}_4\right) reacts with sodium hydroxide \left(\text{NaOH}\right) in an acid-base reaction to form sodium sulfate \left(\text{Na}_2\text{SO}_4\right) and water. Give a balanced equation for the reaction.
[2 marks]
\text{H}_2\text{SO}_4 + \underline{2}\text{NaOH } \rarr \text{Na}_2\text{SO}_4 + \underline{2}\text{H}_2\text{O}
One mark per correctly balanced molecule.
Question 3: Barium sulfate is used as contrast medium in radiography. Its molecular formula is \text{BaSO}_4 (\text{RMM}=233). Calculate the percent by mass of oxygen in the compound.
[2 marks]
There are 4 oxygen atoms in the compound so the relative atomic mass accounted for my oxygen is 4 times the relative atomic mass of oxygen.
\%\text{Mass of Oxygen} = \frac{(4 \times 16)}{233} \times 100 = 27\%
Relative Formula Mass Worksheet and Example Questions
Chemical Measurements and Relative Formula Mass Questions
GCSEOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now