Nanoparticles
Nanoparticles Revision
Nanoparticles
Nanoparticles are particles that are (as the name suggests) very small. Nanoparticles are defined as particles that are between 1 and 100 nm in size (0.000000001 to 0.0000001 metres). To put that into context, the smallest particles that the human eye can see are around 0.058 mm in size, around 58 thousand times larger than a nanoparticle. Nanoparticles can also be defined as particles or molecules containing at a few hundred or so atoms. The study of nanoparticles is a new and exciting field, with applications from medicine to computing.
Relative Sizes of Particles
Once particles shrink to a certain size, it becomes more practical for scientists to begin use smaller units of measurement, instead of using metres. The particles studied in nanoscience are typically around 0.00000001 to 0.000001 metres in size. To save themselves from having to write out all these zeros over and over and over again, researches instead define a smaller unit, the nanometre (nm). 1\text{ nm} is equal to 1 \text{ billion}^{\text{th}} of a metre.
There are 3 categories of small particles that scientist usually refer to. These are:
- Coarse particle ranging from 2,500 to 1\text{ million nm} in size. These are often what we think of as dust and can even be big enough to see with the naked eye. These particles are referred to as \text{PM}_{10}, meaning particulate matter that is less than 10 micrometers in size.
- Fine particles ranging from 100 to 2,500\text{ nm} in size. These particles are referred to as \text{PM}_{2.5}, meaning particulate matter that is less than 25 micrometers in size.
- Nanoparticles, ranging from 1 to 100\text{ nm} in size.
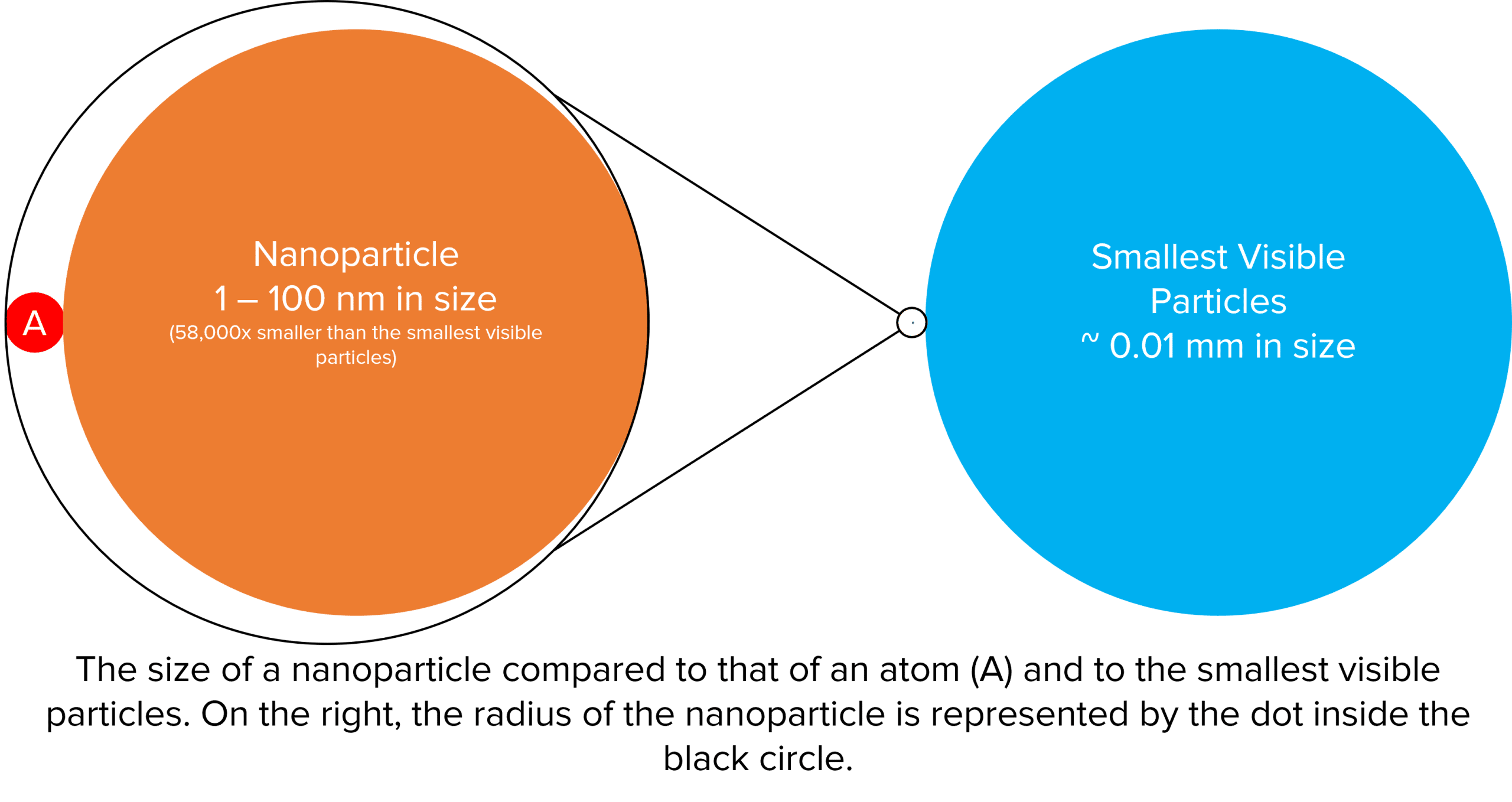
The diagram below demonstrates just how tiny nanoparticles really are. Roughly to scale, it shows a blown up representation of a particle of dust at the very bottom limit of what we can see unaided, next to this (highlighted inside the black circle) is a nanoparticle. To further illustrate its size, the nanoparticle has been blown up and and compared to the size of at atom (the red circle).
Nanoparticle Properties
An interesting feature of particle size is that, as the side of a cube decreases in length by a factor of 10, its surface area to volume ratio increases by a factor of 10. This has important consequences for nanoparticles. The most important result of this is that nanoparticles have a very high surface to volume ratio; the majority of the atoms in a nanoparticle are contained at the surface.
This is a property unique to nanoparticles, as in most other particles, the majority of the atoms are found on the inside of the particle.
One result of this is that nanoparticles of a substance have different chemical and physical properties to that of the substances in bulk. For example, nanoparticles will react much more efficiently than bulk reactants, as there is a far greater proportion of surface layer atoms available for reaction.
Uses of Nanoparticles
The high surface area to volume ratio of nanoparticles means that they tend to make good catalysts. Because substances made up of nanoparticles have a higher surface area than equal masses of substances made up of larger particles, they are able to be used in much smaller quantities when catalyzing reactions.
Nanoparticles may also have medical applications. Nanoparticles of silver have antibacterial properties. Added to the polymer fibers of face masks or bandages, they can be used to reduce the spread of diseases. Nano particles are also absorbed more easily in the body, making them good drug delivery vehicles. However, the effects of nanoparticles on human health are not yet fully understood. Before they can be used more widely they must be thoroughly tested.
Some nanoparticles are able to conduct electricity. This means they can be used in the development of tiny circuits for use in miniaturized computing.
Note:
Converting between Units
Chemistry is all about what happens at the small scale. Atoms are, to say the least, very very small, as are many particles. In general, most chemistry tends to happen on the nano- through to the mili-scale. As such, it is important that anyone who wants to understand chemistry be able to convert between the more common day to day units (think centimetre, litre, gram) and those used frequently in chemistry. Firstly, it is important to understand what the unit prefixes (the letters before a unit, e.g. the \text{k} in \text{kg} or \text{n} in \text{nm}) mean. This prefix tells us by what to multiply or divide the quantity to get in its standard unit.
| Prefix: |
Mega (\text{M}) |
Kilo (\text{k}) |
Unit
|
Deci (\text{d}) |
Centi (\text{c}) |
Milli (\text{m}) |
Micro (\mu) |
Nano (\text{n}) |
| Multiplied/divided by: | \times 1,000,000 (10^6) | \times 1,000 (10^3) | 0 | \div 10\text{ } | \div 100 (10^{-2}) | \div 1000 (10^{-3}) | \div 1,000,000 (10^{-6}) | \div 1,000,000,000 (10^{-9}) |
This table can be used to help convert between two unit scales.
Example 1: Converting to base units
Convert 54.5\text{ kg} to grams.
- The unit prefix here is \text{k}, that means we are working with kilograms.
- Kilograms means means we are multiplying the number of grams by \textcolor{#00bfa8}{1000} (e.g. 1\text{ kg = }1000\text{ g})
- To get 54.5\text{ kg} into \text{g} we need to multiply by 1000:
54.5\text{ kg}\times \textcolor{#00bfa8}{1000}\text{ = } \textcolor{#008d65}{54,500\text{ g}}
Example 2: Converting between units
Convert 13\text{ cm} to \text{nm}.
- This is trickier to do all in one as the table above does not tell us what to divide a centimetre by to get a nanometre.
- Firstly, we can convert the centimetre back into metres. We know from the prefix that we are working in centimetres, this means that to get to metres, we need to divide by \textcolor{#00bfa8}{100}.
13\text{ cm}\div \textcolor{#00bfa8}{100} = \textcolor{#008d65}{0.13\text{ m}}
- From metres, we need to get to nanometres, using the method from Example 1 we know that to get to metres, we multiply by \textcolor{#f21cc2}{1,000,000,000 (10^9)}:
0.13\text{ m}\times \textcolor{#f21cc2}{1,000,000,000} = \textcolor{#008d65}{1.30 \times 10^8\text{ nm}}
Nanoparticles Example Questions
Question 1: Why are the properties of nanoparticles different to the bulk properties of a material of the same substance?
[3 marks]
- As the size of particle decreases by a factor of 10, its surface area to volume ratio increases by a factor 10.
- This means that for nanoparticles, the majority of atoms are at the surface of the molecule.
- This affects the properties of the particle.
Question 2: Convert 1.5\text{ } \mu\text{g} into grams.
[3 marks]
From the table above, we know that μg means micrograms.
This is 1\text{ g} divided by 1,000,000
\frac{1.5}{1,000,000} = 0.0000015\text{ g}Questions 3: Convert 4.7\text{ km} to \text{cm}.
[3 marks]


