Moving Charges
Moving Charges Revision
Moving Charges
Instead of considering the force acting on a current carrying wire, we may also need to consider the force acting on a single moving charged particle.
Force on a Charged Particle
If a charged particle (such as a proton or electron) is passed through a magnetic field, the charged particle will experience a force. The direction of the force can be calculated using Fleming’s left hand rule. However, for an electron the direction of current would be opposite to the direction of electron flow as current is defined as the rate of flow of positive charge.
The magnitude of the force may be calculated using:
F = BQv
- F is the force on the charged particle in newtons \left(\text{N}\right).
- B is the magnetic flux density in tesla \left(\text{T}\right).
- Q is the charge of the particle in coulombs \left(\text{C}\right).
- v is the speed of the moving charged particle in metres per second \left(\text{ms}^{-1}\right).
As with the previous equation, all three variables must be at right angles (perpendicular) to each other to achieve maximum force. No force will be experienced if current and magnetic flux density are parallel.
Example: An electron passes perpendicular to a magnetic field. Given that the magnetic flux density is 0.5 \: \text{T} and the electron moves at a velocity of 6 \times 10^7 \: \text{ms}^{-1}, calculate the force on the electron.
[3 marks]
F = BQv
F = 0.5 \times 1.6 \times 10^{-19} \times 6 \times 10^7
F = 4.8 \times 10^{-12} \: \text{N}
Cyclotrons
A cyclotron is a type of particle accelerator that makes use of magnetic fields and electric fields to accelerate charged particles.
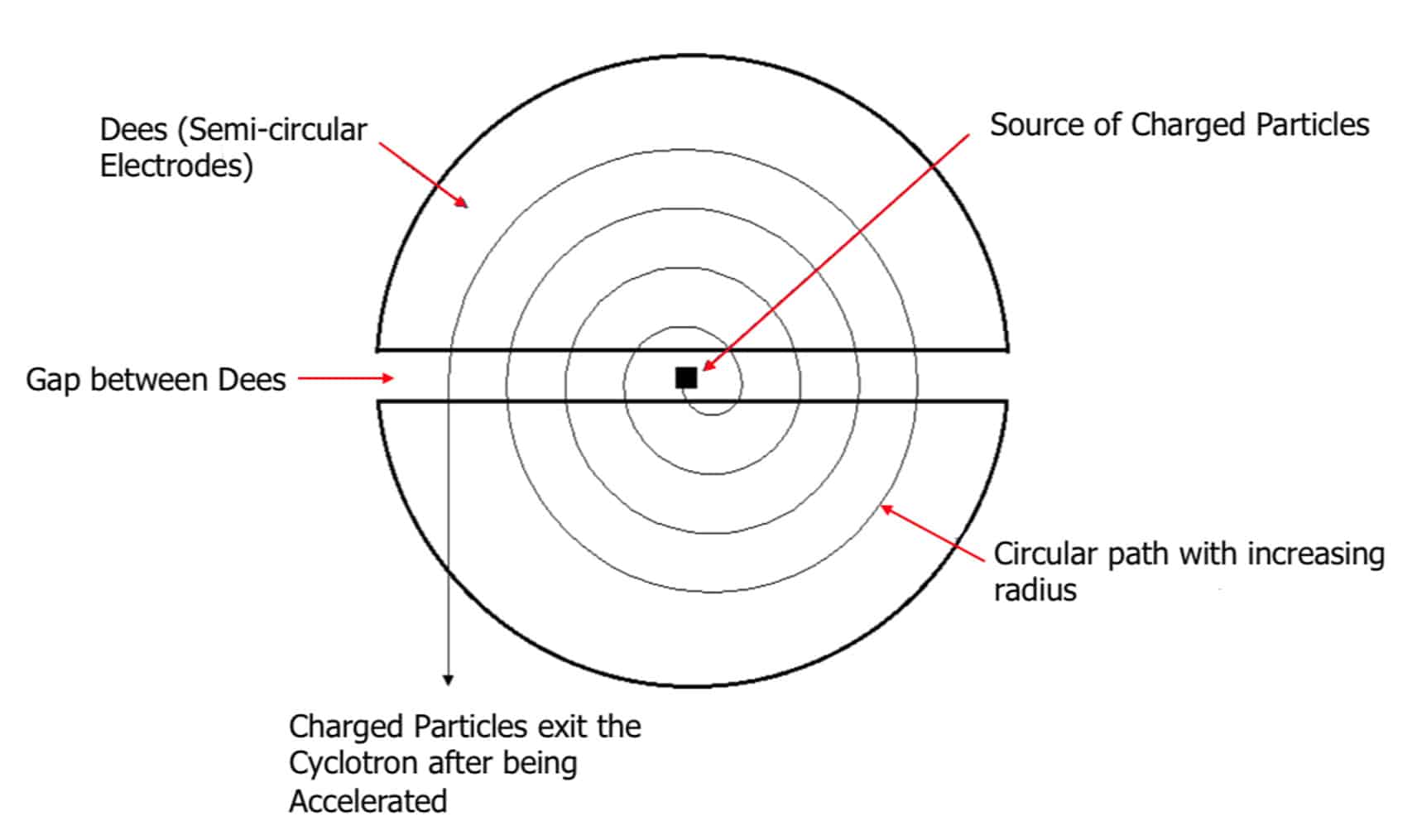
A source of charged particles is released at the centre of the cyclotron into one of the Dees. The magnetic field within the Dees always acts towards the centre and perpendicular to the motion of the charged particle. The magnetic field accelerates the particle but it does not change the speed. Instead, it only changes the direction of the particle.
When the particle leaves the Dee, it is accelerated across the gap by an electric field. As velocity has increased, the particle now takes a path with a greater radius than before and leaves the electrode again. The process repeats, repeatedly accelerating the particle.
The radius of the path of the charged particle is determined by its velocity. The centripetal force is caused by the force of the magnetic field in the charged particle. These forces must be balanced in order for the charged particle’s radius to remain constant.
Therefore we can equate the centripetal force equation with the force of a magnetic field equation to give:
\dfrac{mv^2}{r} = BQv
As there is a v on both sides of the equation we can cancel these out to give:
\dfrac{mv}{r} = BQ
Rearranging to make r the subject gives:
r = \dfrac{mv}{BQ}
This shows that the radius of the charged particle is proportional to the mass of the particle (which would be constant) and the velocity the particle is travelling at. It also shows the radius is inversely proportional to the charge of the charged particle and the magnetic flux density.
Moving Charges Example Questions
Question 1: A proton passes perpendicular to a magnetic field. Given that the magnetic flux density is 0.2 \: \text{T} and the proton moves at a velocity of 1.1 \times 10^7, calculate the force on the electron.
[3 marks]
Question 2: Describe how a cyclotron uses magnetic fields.
[2 marks]
The magnetic fields in a cyclotron are used to keep the charged particle in circular motion. As the magnetic field acts perpendicular to motion, it acts as a centripetal force keeping the radius inside the Dee constant for each time it enters the Dee.
Question 3: A charged particle is accelerated so that its velocity doubles every time it passes the gap between the Dees. After crossing the gap 5 times, how much has the radius of the circular motion increased?
[3 marks]
As r =\dfrac{mv}{BQ}, radius and velocity are proportional. Therefore, the radius also doubles each time it crosses between the Dees. So after 5 times, the radius will increase by 2^5 times = 32 times.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.