Magnetic Flux and Flux Linkage
Magnetic Flux and Flux Linkage Revision
Magnetic Flux and Flux Linkage
To understand electromagnetic induction, we first must understand what magnetic flux and flux linkage are.
Magnetic Flux
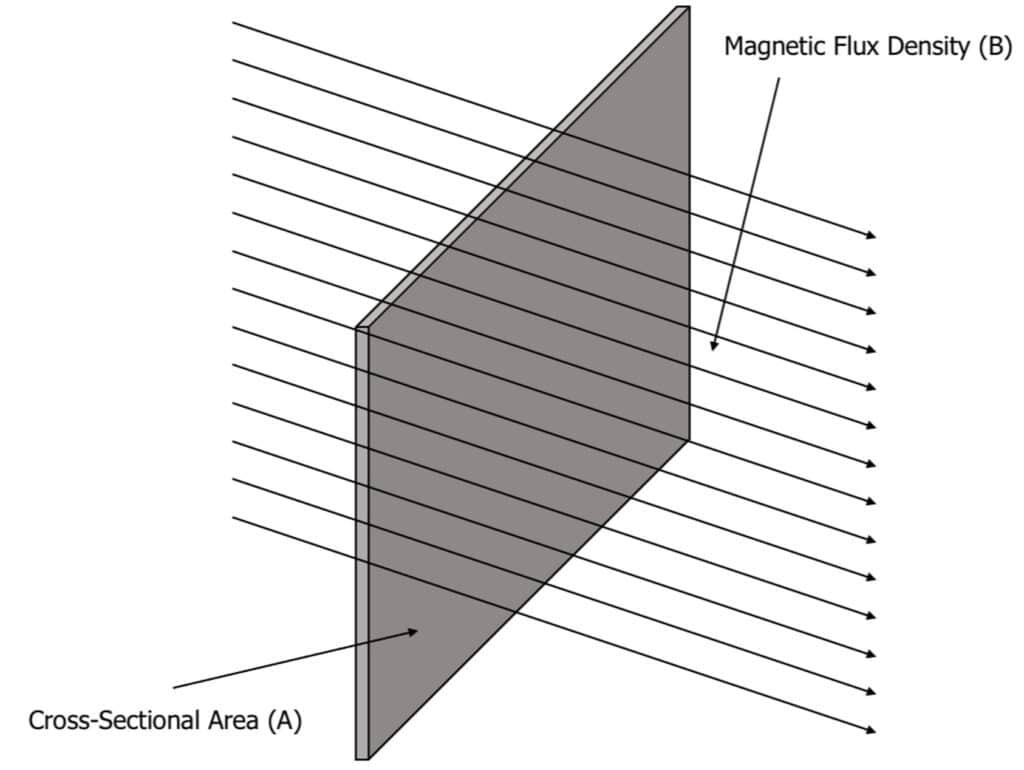
When a wire passes through a magnetic field, the wire cuts through the magnetic field lines. The magnetic flux is the total amount of magnetic field that the wire passes through as it passes through the magnetic field.
As with the force in a magnetic field, if the conducting wire passes through the field at 90 degrees (perpendicular), the maximum amount of magnetic flux is measured. If the wire passes through parallel to the magnetic field, magnetic flux is zero.
The magnetic flux \left(\Phi\right) could also be defined as the number of magnetic field lines being cut through a given area by a conductor. As an equation, this can be written:
\Phi = BA
- \Phi is the magnetic flux measured in Webers \left(\text{Wb}\right).
- B is the magnetic flux density in Tesla \left(\text{T}\right).
- A is the cross-sectional area in metres squared \left(\text{m}^2\right).
This equation can only be used when the magnetic flux is perpendicular to the cross-sectional area of the conductor, as in the diagram above.
Alternatively, if the cross-sectional area and magnetic flux are not perpendicular, the equation below can be used:
\Phi = BA \cos \theta
where \theta is the angle between the cross-sectional area and the magnetic field.
Example: A wire of cross sectional 0.001 \text{m}^2 cuts through a magnetic field with density 2 \times 10^{-3} \: \text{T}. Calculate the magnetic flux density and give the appropriate units.
[2 marks]
\Phi = BA
\Phi = 2 \times 10^{-3} \times 0.001
\Phi = 2 \times 10^{-6} \: \text{Wb}
Magnetic Flux Linkage
The magnetic flux density and the force produced by a single wire is usually very low. Instead, using a coil of wire increases the cross sectional area and increases the magnetic flux density produced.
The magnetic flux linkage refers to the number of turns on a coil and multiples this by the magnetic flux of one wire. This gives the equation:
N\Phi = BAN
where N is the number of turns on a coil.
Again, if the cross-sectional area and magnetic flux are not perpendicular, the equation below can be used:
N \Phi = BAN \cos \theta
where \theta is the angle between the cross-sectional area and the magnetic field.
Example: A solenoid contains 250 turns of wire. Each piece of wire has a cross sectional area of 0.002 \text{m}^2. If the magnetic flux density is 8.0 \: \text{mT}, calculate the magnetic flux linkage.
[2 marks]
N\Phi = BAN
N\Phi = 8.0 \times 10^{-3} \times 0.002 \times 250
N\Phi = 4 \times 10^{-3} \: \text{Wb turns}
Required Practical 11
Investigating Magnetic Flux Linkage.
A search coil and oscilloscope can be used to investigate the effect of varying the angle between the search coil and a magnetic field on magnetic flux linkage. The equipment is shown below:
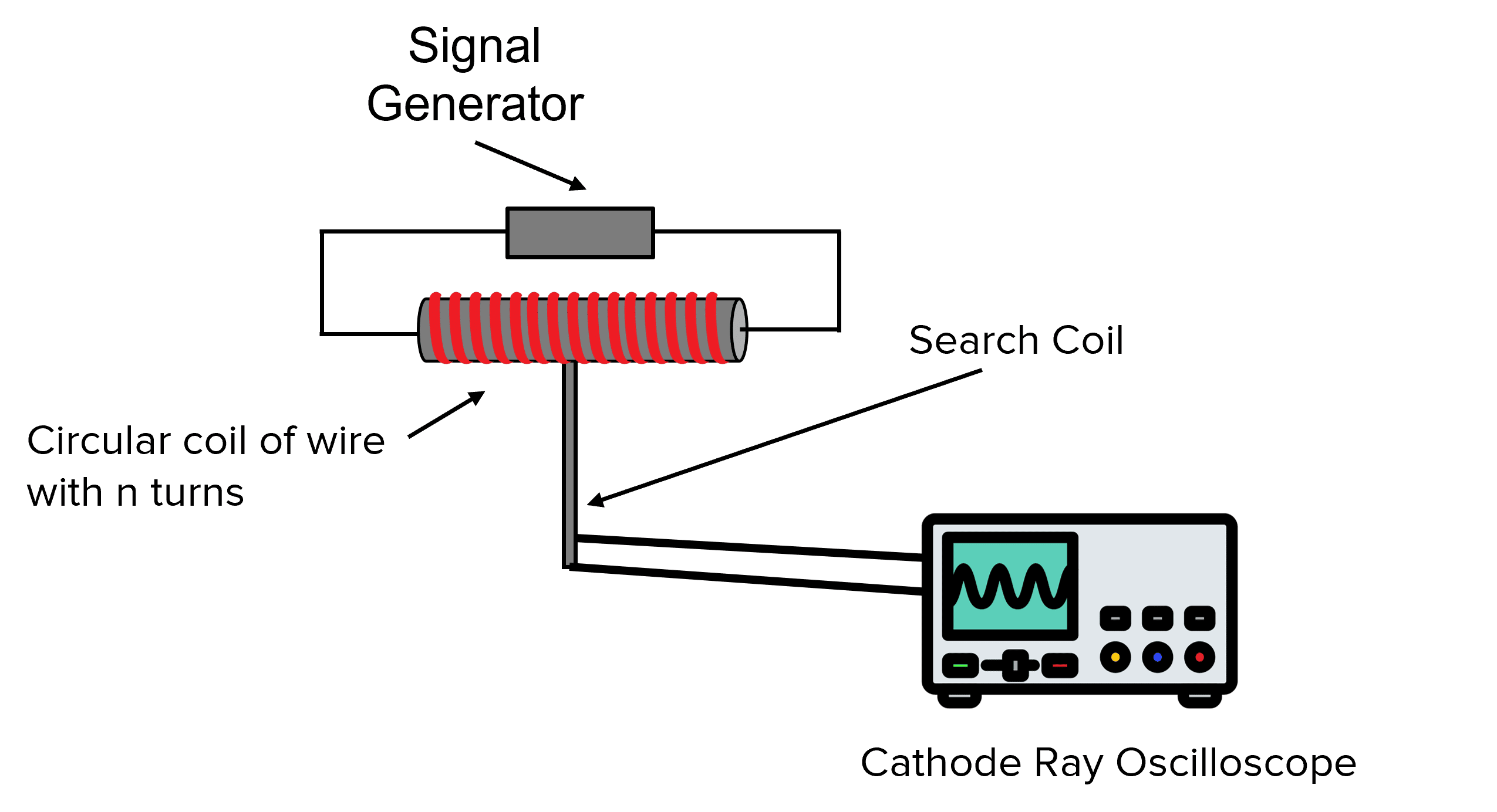
The circular coil of wire creates a uniform magnetic field of which the search coil is rotated within. The oscilloscope will display the varying EMF produced as the search coil rotates within the coil of wire.
When experimenting, the peak EMF will be determined when the search coil is perpendicular to the magnetic field of the coil of wire. A reading can then be taken every 10 \degree of rotation of the search coil.
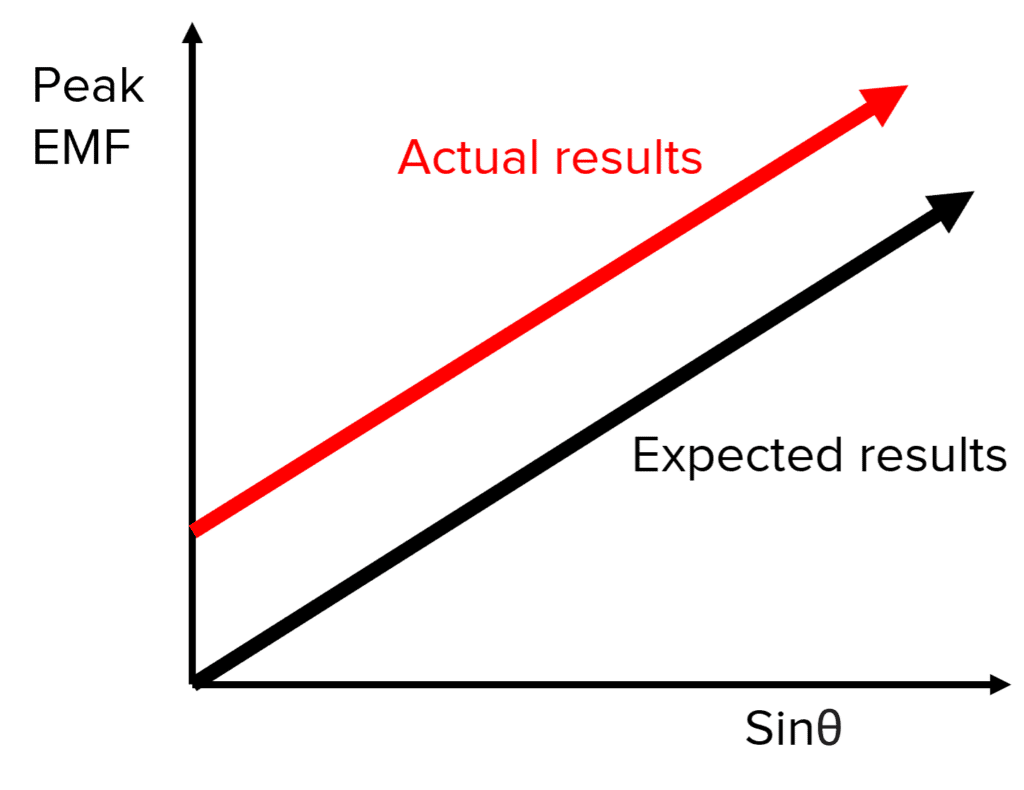
The graph here may be plotted to show the relationship between peak EMF and the rotation of the search coil. \theta is the angle of rotation.
It is likely that the y-intercept of our experimental results will not be zero when the search coil and coil of wire are parallel. This is because of a degree of human error when trying to make sure the wires and search coil are parallel.
Magnetic Flux and Flux Linkage Example Questions
Question 1: A wire of cross sectional area 0.005 \: \text{m}^2 cuts through a magnetic field with density 5 \times 10^{-3} \: \text{T}. Calculate the magnetic flux density and give the appropriate units.
[2 marks]
Question 2: Describe why a solenoid would produce a greater magnetic flux than a single loop of wire.
[2 marks]
A coil of wire (solenoid) would increase the cross-sectional area compared to a single loop of wire. We can see this in the equation \Phi = BA where \Phi and A are proportional.
Question 3: A solenoid contains 500 turns of wire. Each piece of wire has a cross sectional area of 0.010 \: \text{m}^2. If the magnetic flux density is 12.0 \: \text{mT}, calculate the magnetic flux linkage.
[2 marks]
You May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
