Electromagnetic Induction
Electromagnetic Induction Revision
Electromagnetic Induction
When a conductor moves through a magnetic field, an electromotive force (EMF) is induced in the conductor. This is known as electromagnetic induction.
Electromagnetic Induction
As the conductor cuts through the magnetic field lines, it causes a change in magnetic flux which causes work to be done. This energy is transformed to electrical energy, causing a current to be induced. Importantly, this process can be harnessed in transformers and generators.
This phenomenon can be shown experimentally:
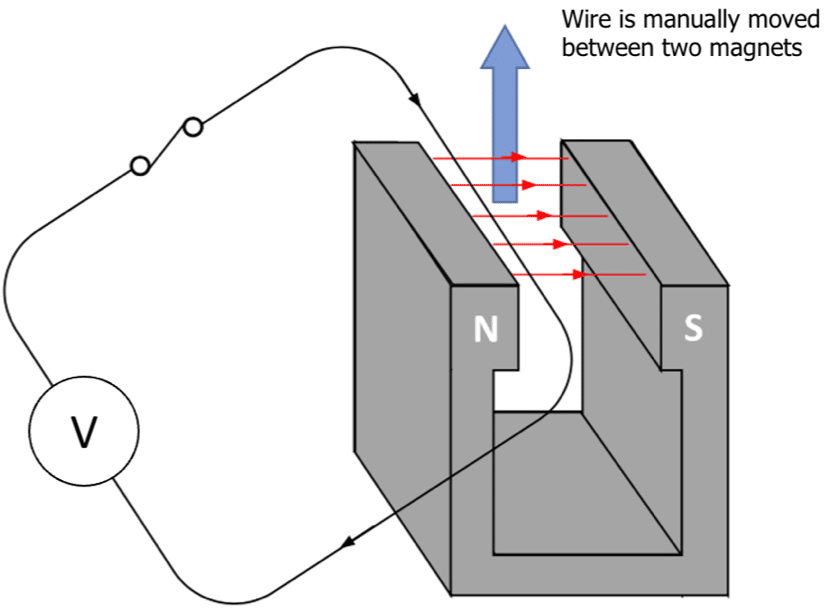

When the wire is stationary (either inside the magnetic field or outside), no voltage is shown on the sensitive voltmeter. This shows no EMF is induced as there is no change in magnetic flux.
When the wire is moved between the magnets, through the magnetic field, a reading can be seen on the voltmeter. This is because the wire cuts the magnetic field lines and causes a change in magnetic flux. Therefore an EMF is induced.
Moving the wire faster, increasing the length of the wire or increasing the strength of the magnets results in an increase in induced EMF as they all cause a greater change in magnetic flux.
Faraday’s Law
Faraday’s law can be observed in the experiment above. Faraday’s law states that magnitude of the induced EMF is proportional to the rate of change of magnetic flux linkage.
As previously shown, the faster the wire moved through the magnetic field, the greater the strength of the magnet or the longer the wire, all increase the magnitude of EMF produced as the all increase the rate of change of magnetic flux linkage.
Lenz’s Law
Lenz’s Law can also be shown experimentally. Lenz’s law states that the induced EMF acts in a direction to oppose the change that causes it.
Lenz’s law can be shown by passing a bar magnet through a coil of wire attached to a sensitive ammeter. The sensitive ammeter will deflect in opposing directions as the bar magnet is passed through the coil in opposite directions.
Induced EMF
By combining Faraday’s law and Lenz’s law, an equation can be formed to calculate the induced EMF:
\epsilon = -N \dfrac{\Delta \Phi}{\Delta t}
- \epsilon is the induced EMF in volts \left(\text{V}\right).
- N is the number of turns on the coil.
- \Delta \Phi is the change in magnetic flux in Webers \left(\text{Wb}\right).
- \Delta t is the change in time in seconds \left(\text{s}\right).
The minus sign represents Lenz’s law as it shows the direction of the induced EMF will oppose the direction of the bar magnet.
Example: Calculate the EMF induced when a coil of wire with 200 turns creates a change in magnetic flux of 8 \times 10^{-6} \: \text{Wb} in 2 \: \text{ms}.
[2 marks]
\epsilon = -N \dfrac{\Delta \Phi}{\Delta t}
\epsilon = -200 \times \dfrac{8 \times 10^{-6}}{2 \times 10^{-3}}
\epsilon = -0.8 \: \text{V}
Rotating Coil
If a coil is rotating uniformly in a magnetic field, an EMF is induced. This is because we have a conductor that is constantly cutting the magnetic field lines, and the angle between the conductor and the field lines is constantly changing.
Using the principles of circular motion, the EMF induced as a result of this rotation can be calculated using the equation:
\epsilon = BAN \omega \sin \omega t
- \epsilon is the induced EMF in volts \left(\text{V}\right).
- B is the magnetic flux density in Tesla \left(\text{T}\right).
- A is the cross-sectional area in metres squared \left(\text{m}^2\right).
- N is the number of turns on the coil.
- \omega is the angular velocity of the rotating coil \left(\text{rad s}^{-1}\right).
- t is the time in seconds \left(\text{s}\right).
Electromagnetic Induction Example Questions
Question 1: Describe a simple experiment that would allow you to demonstrate electromagnetic induction.
[2 marks]
Passing a current carrying wire attached to a sensitive voltmeter through a magnetic field will show electromagnetic induction. When the wire is stationary, no voltage is detected. As the wire moves, a voltage is detected showing that an EMF is induced.
Question 2: State Faraday’s law and Lenz’s law.
[2 marks]
- Faraday’s law – the magnitude of the induced EMF is proportional to the rate of change of magnetic flux linkage.
- Lenz’s law – the direction of the induced EMF is such that it opposes the change that causes it.
Question 3: Calculate the EMF induced when a coil of wire with 400 turns creates a change in magnetic flux of 9 \times 10^{-6} \: \text{Wb} in 6 \: \text{ms}.
[2 marks]
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.