Alternating Currents
Alternating Currents Revision
Alternating Currents
The mains electricity supply is alternating current (A.C). This section looks at the features of A.C including frequency, root-mean-square current and root-mean-square voltage.
Alternating Currents
Alternating current (A.C) periodically varies from positive to negative current. If the alternating current supply is plotted against time, a sinusoidal graph is formed showing that the electrons in the wire move back and forth in simple harmonic motion (SHM). The same concept could be used for plotting voltage against time.
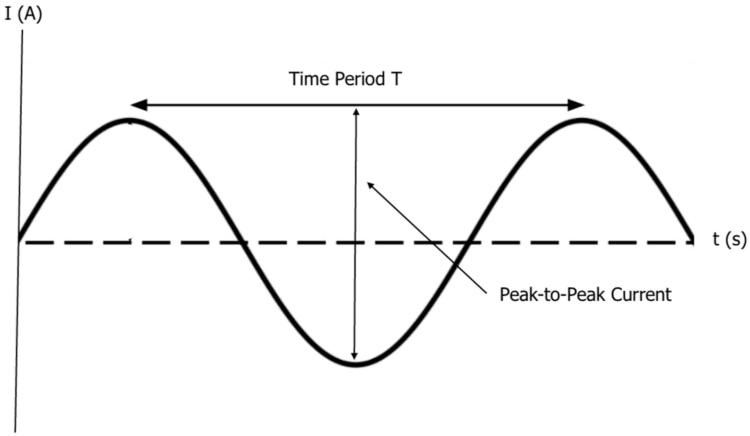
The time period can be seen above on the graph and is the time difference between two peak positive currents or two peak negative currents. Frequency of the AC supply can also be calculated as:
f = \dfrac{1}{T}
- f is the frequency in Hertz \left(\text{Hz}\right).
- T is the time period in seconds \left(\text{s}\right).
Example: The time period of an AC supply is 0.1 \: \text{s}. Calculate the frequency of the supply.
[1 mark]
f = \dfrac{1}{T}
f = \dfrac{1}{0.1}
f = 10 \: \text{Hz}
Root-Mean-Square Current
Root-Mean-Square (rms) is used to compare AC and DC (Direct Current) currents. The rms for direct current or voltage represents the value of direct current or voltage that will produce the same power dissipation as alternating current. The rms value is calculated by the square root of the mean of the squares of all values of voltage in one full cycle.
To calculate the rms current \left(I_{rms}\right), the following equation can be used:
I_{rms} = \dfrac{I_0}{\sqrt{2}}
where I_{rms} is the rms current and I_0 is the peak current. Both are measured in amps \left(\text{A}\right).
To calculate the rms voltage \left(V_{rms}\right), the following equation can be used:
V_{rms} = \dfrac{V_0}{\sqrt{2}}
where V_{rms} is the rms voltage and V_0 is the peak voltage. Both are measured in volts \left(\text{V}\right).
Example: The peak current read from an oscilloscope trace is 2.5 \: \text{A}. What is the rms current?
[1 mark]
I_{rms} = \dfrac{I_0}{\sqrt{2}}
I_{rms} = \dfrac{2.5}{\sqrt{2}}
I_{rms} = 1.8 \: \text{A}
Applications of Alternating Current
The UK power supply is an alternating current/voltage. It has a peak voltage of 230 \: \text{V} and the frequency of the alternating voltage is 50 \: \text{Hz} (switches from positive to negative 50 times per second). However, this is an average and varies depending upon the time of day, demand and type of consumer.
Alternating Currents Example Questions
Question 1: What is meant by rms current?
[2 marks]
The square root of the mean of the squares of all values of voltage in one full cycle.
Question 2: The peak current read from an oscilloscope trace is 5.25 \: \text{A}. What is the rms current?
[1 mark]
Question 3: Give 2 factors that affect the peak voltage of the mains supply.
[2 marks]
Any two from:
- Time of day
- Demand
- Type of consumer
Alternating Currents Worksheet and Example Questions
Alternating Current Questions
A LevelOfficial MMEYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.