Energy Stored by a Capacitor
Energy Stored by a Capacitor Revision
Energy Stored by a Capacitor
Capacitors are very useful when a quick release of energy is needed. This section looks at how we can calculate the amount of energy stored by a capacitor or the amount of energy released by a capacitor when discharging.
Energy Stored by a Capacitor
As the capacitor charges, it stores electrical energy which can later be released. In the process of charging, electrons are moved from the positive plate to the negative plate.
As the negative plate becomes more charged, the electrostatic force of repulsion increases, meaning that the circuit needs to do work on the electrons to overcome the electrostatic force.
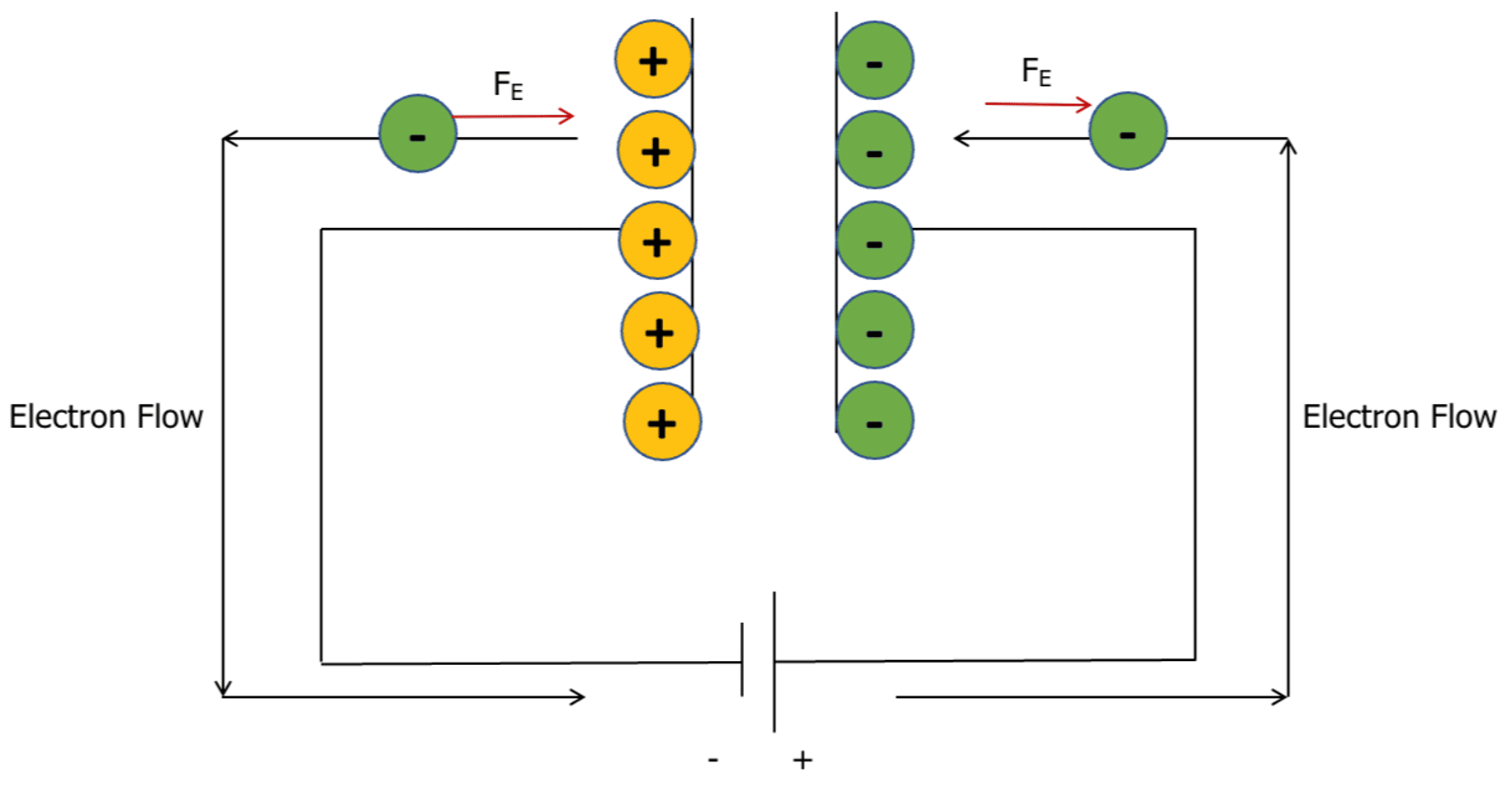
Therefore, the charge on the capacitor is directly proportional to the potential difference of the power supply.
If we were to plot the Potential Difference against the Charge for a parallel plate capacitor, it would look something like this:
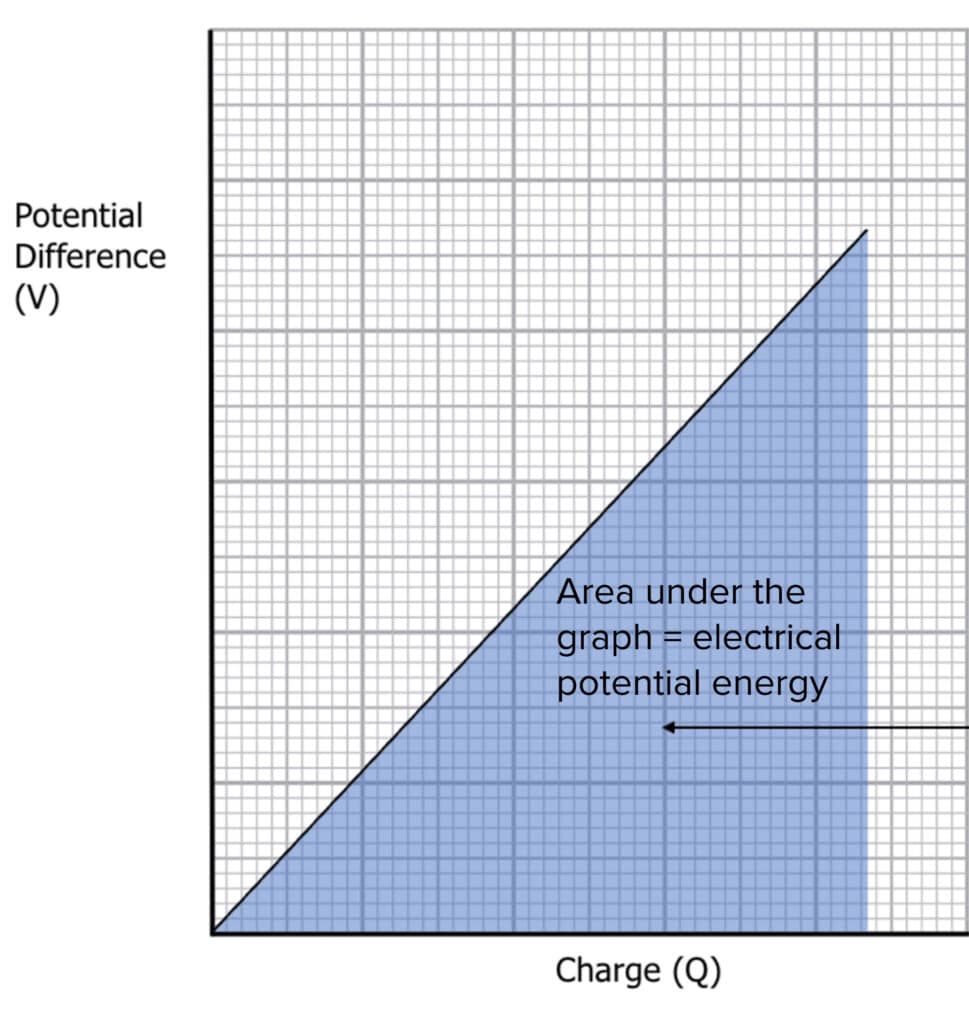

The energy stored by a capacitor (electrical potential energy) is equal to the area under the potential difference-charge graph. The area of a triangle is \dfrac{1}{2} \times \text{base} \times \text{height}, and therefore we can write the energy stored by the capacitor as:
E = 0.5QV
We can substitute in the capcitance equation, \left(Q=CV\right):
E = 0.5 CV^2
Both these equations can be used to calculate the energy stored by a capacitor.
Example: A capacitor of capacitance 2 \: \mu \text{C} requires a potential difference of 75 \: \text{kV} to fully charge. How much electrical potential energy does it store when fully charged?
[2 marks]
E = 0.5 CV^2
E = 0.5 \times 2 \times 10^{-6} \times 75000^2
E = 5625 \: \text{J}
Energy Stored by a Capacitor Example Questions
Question 1: Explain the process of how a capacitor charges.
[2 marks]
In the process of charging, electrons are moved from the positive plate to the negative plate. As the negative plate becomes more charged, the electrostatic force of repulsion increases, meaning that the circuit needs to do work on the electrons to overcome the electrostatic force.
Question 2: A capacitor of capacitance 1.2 \: \mu \text{F} requires a potential difference of 50 \: \text{kV} to fully charge. How much electrical potential energy does it store when fully charged?
[2 marks]
Question 3: The charge on a capacitor is 3 \: \mu \text{C} when the potential difference is 150 \: \text{kV}. Calculate the electric potential energy of the capacitor.
[2 marks]
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.