Vector Calculations
Vector Calculations Revision
Vector Calculations
Being able to use vectors in calculations is a key skill in A-Level, this section will cover the following areas of vector calculations:
- Finding vector magnitudes using Pythagoras’ theorem
- Resolving vectors into component form
- Finding the distance between points using a vector’s magnitude
- Using the cosine rule to find the angle between two vectors
Make sure you are happy with the following topics before continuing.
Finding Vector Magnitudes Using Pythagoras’ Theorem
Notation: The magnitude of vector \boldsymbol{a} is written as |\boldsymbol{a}|, similarly the magnitude of \overrightarrow{AB} is written as |\overrightarrow{AB}|.
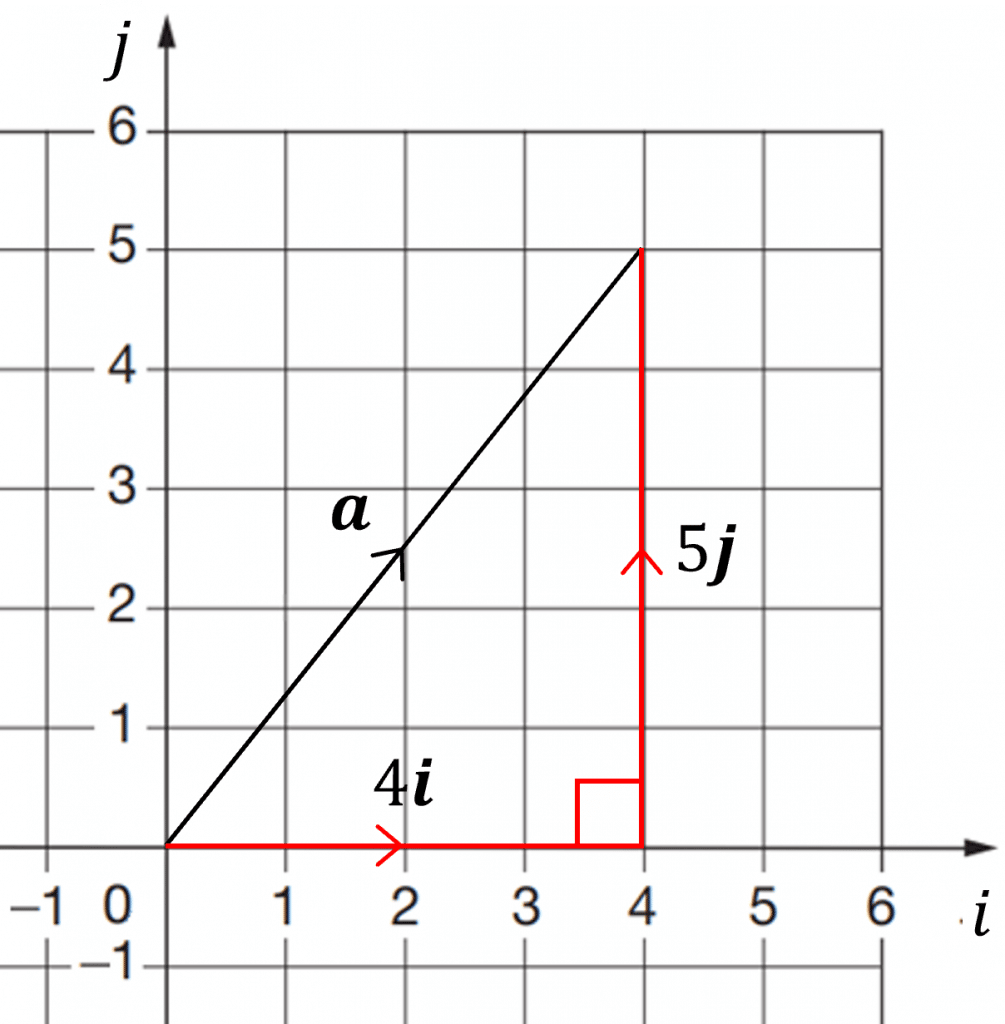

As shown on the image on the right, the \boldsymbol{i} and \boldsymbol{j} components of a vector create a right-angled triangle, this means you can use Pythagoras’ theorem to find the magnitude (length) of the vector.
Using Pythagoras’ theorem we can calculate the magnitude of vector \boldsymbol{a}:
|\boldsymbol{a}|=\sqrt{4^2+5^2}=\sqrt{41}Sometimes you may be required to find a unit vector in the direction of a particular vector, which can be found using:
Unit vector in the direction of a vector \boldsymbol{a}=\dfrac{\boldsymbol{a}}{|\boldsymbol{a}|}
As stated in position vectors, a unit vector has a magnitude of 1
Example: Find the unit vector in the direction of \boldsymbol{m}=-3\boldsymbol{i}+6\boldsymbol{j}
We first need to find the magnitude of \boldsymbol{m}:
|\boldsymbol{m}|=\sqrt{(-3)^2+6^2}=\sqrt{9+36}=3\sqrt{5}Therefore, the unit vector in the direction of \boldsymbol{m} is:
\dfrac{\boldsymbol{m}}{|\boldsymbol{m}|}=\dfrac{\boldsymbol{m}}{3\sqrt{5}}=\dfrac{1}{3\sqrt{5}}(-3\boldsymbol{i}+6\boldsymbol{j})
Resolving Vectors into Component Form
When calculating with vectors it is easier to work with them when they are separated into \boldsymbol{i} and \boldsymbol{j} vectors, allowing you to work with one component at a time.
Splitting a vector into components is called resolving the vector, which can be done using both trigonometry and Pythagoras’ theorem.
Example: An object is travelling at 11\text{ ms}^{-1} at an angle of 38\degree to the horizontal.
Find the horizontal (\boldsymbol{i}) and vertical (\boldsymbol{j}) components of the object’s velocity, \boldsymbol{v}.
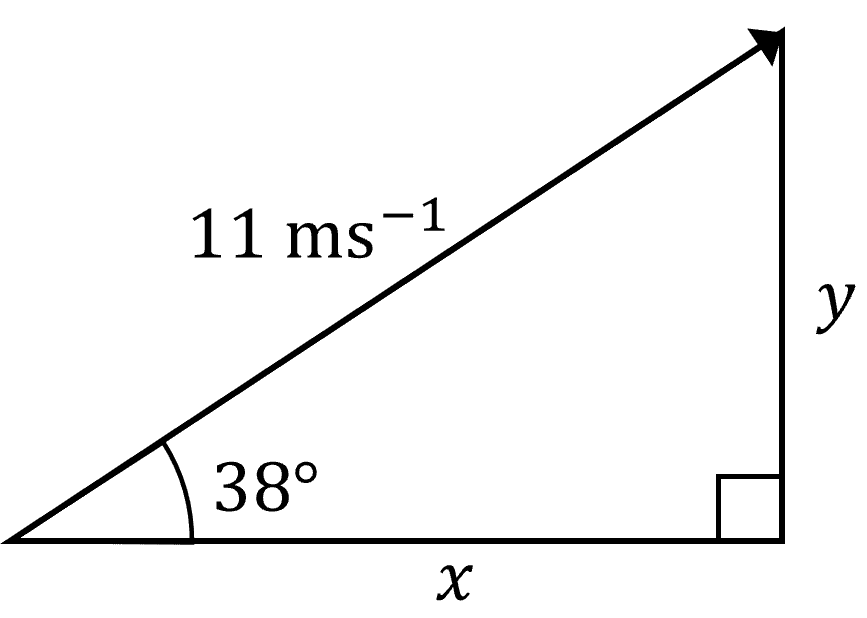

It is often easier to draw a diagram and make a right angled triangle for the problem:
We can then use trigonometry to find x and y:
\cos{38\degree}=\dfrac{x}{11} \rArr x=11\cos{38\degree}
\sin{38\degree}=\dfrac{y}{11} \rArr y=11\sin{38\degree}
Thus,
\begin{aligned} \boldsymbol{v}&=(11\cos{38\degree}\boldsymbol{i}+11\sin{38\degree}\boldsymbol{j})\text{ ms}^{-1} \\&=(8.67\boldsymbol{i}+6.77\boldsymbol{j})\text{ ms}^{-1} (2\text{ dp}) \end{aligned}
Finding the Distance Between Points Using a Vector’s Magnitude
Calculating the distance between two points is fairly straight forward, you need to find the vector between them and then calculate its magnitude using Pythagoras’ theorem.
Example: The position vectors of points K and L are 6\boldsymbol{i}-2\boldsymbol{j} and -3\boldsymbol{i}+5\boldsymbol{j} respectively.
Find the distance between the points K and L, giving your answer to 2 decimal places.
First, we need to find the vector \overrightarrow{KL}
\overrightarrow{KL}=-3\boldsymbol{i}+5\boldsymbol{j}-(6\boldsymbol{i}-2\boldsymbol{j})=-9\boldsymbol{i}+7\boldsymbol{j}Then calculate the magnitude of \overrightarrow{KL}:
|\overrightarrow{KL}|=\sqrt{(-9)^2+7^2}=\sqrt{130}=11.40 \, (2\text{ dp})
Using the Cosine Rule to Find the Angle Between Two Vectors
To find the angle between two vectors, \boldsymbol{a} and \boldsymbol{b}, you can construct a triangle with \boldsymbol{a} and \boldsymbol{b} as two of the sides and then calculate the magnitude of \overrightarrow{AB} for the remaining side. You can use the cosine rule to find the angle between the two vectors.
Example: \overrightarrow{OA}=4\boldsymbol{i}+\boldsymbol{j} and \overrightarrow{OB}=-2\boldsymbol{i}+5\boldsymbol{j}
Find the angle \theta between the vectors \overrightarrow{OA} and \overrightarrow{OB}, giving your answer to 2 decimal places.
We first need to calculate the magnitudes of the vectors, \overrightarrow{OA},\overrightarrow{OB} and \overrightarrow{AB}, so we can construct a triangle.


|\overrightarrow{OA}|=\sqrt{4^2+1^2}=\sqrt{17}
|\overrightarrow{OB}|=\sqrt{(-2)^2+5^2}=\sqrt{29}
\begin{aligned} |\overrightarrow{AB}| &=|\overrightarrow{OB}-\overrightarrow{OA}| \\ &=|-2\boldsymbol{i}+5\boldsymbol{j}-(4\boldsymbol{i}+\boldsymbol{j})|\\ &=|-6\boldsymbol{i}+4\boldsymbol{j}| \\ &=\sqrt{(-6)^2+4^2}=2\sqrt{13} \end{aligned}
Then using the cosine rule to find angle \theta:
\cos{\theta}=\dfrac{(\sqrt{17})^2+(\sqrt{29})^2-(2\sqrt{13})^2}{2\times \sqrt{17} \times \sqrt{29}}=\dfrac{-3}{\sqrt{493}}
\rArr \theta=\cos ^{-1} \left(\dfrac{-3}{\sqrt{493}} \right)=97.77 \degree \, (2\text{ dp})
Vector Calculations Example Questions
Question 1: Find the unit vector in the direction of \boldsymbol{t}=4\boldsymbol{i}-5\boldsymbol{j}
[2 marks]
First find the magnitude of \boldsymbol{t}:
|\boldsymbol{t}|=\sqrt{4^2+(-5)^2}=\sqrt{16+25}=\sqrt{41}
Therefore, the unit vector is:
\dfrac{\boldsymbol{t}}{|\boldsymbol{t}|}=\dfrac{\boldsymbol{t}}{\sqrt{41}}=\dfrac{1}{\sqrt{41}}(4\boldsymbol{i}-5\boldsymbol{j})
Question 2: Point S has position vector \dbinom{4}{-3} and point T has position vector \dbinom{-5}{2}. Find the distance between points S and T, giving your answer to 2 decimal places.
[2 marks]
First, we need to find the vector \overrightarrow{ST} between the points.
\overrightarrow{ST}=\dbinom{-5}{2}-\dbinom{4}{-3}=\dbinom{-5-4}{2-(-3)}=\dbinom{-9}{5}
So, |\overrightarrow{ST}|=\sqrt{(-9)^2+5^2}=\sqrt{106}=10.30 \, (2 \text{ dp})
Question 3: A vector \boldsymbol{w} models the movement of an object. The object is travelling at a speed of 8\text{ ms}^{-1} with direction of 25\degree above the horizontal.
Write \boldsymbol{w} in component form, giving the coefficients of \boldsymbol{i} and \boldsymbol{j} to 2 decimal places.
[2 marks]
It is first useful to draw a diagram of the vector \boldsymbol{w}, forming a right-angled triangle.

Now we can use trigonometry to find x and y:
\cos{25\degree}=\dfrac{x}{8} \rArr x=8\cos{25\degree}
\sin{25\degree}=\dfrac{y}{8} \rArr y=8\sin{25\degree}
So,
\begin{aligned} \boldsymbol{w}&=8\cos{25\degree}\boldsymbol{i}+8\sin{25\degree}\boldsymbol{j}\\ &=7.25\boldsymbol{i}+3.38\boldsymbol{j}\end{aligned}
Question 4: The points X, Y and Z form a triangle, and have position vectors 2\boldsymbol{i}+3\boldsymbol{j}, -\boldsymbol{i}+2\boldsymbol{j} and 4\boldsymbol{i}-2\boldsymbol{j} respectively. Find the angle, \theta between vectors \overrightarrow{YZ} and \overrightarrow{ZX}, giving your answer to 2 decimal places.
[4 marks]
We first need to find the following vectors: \overrightarrow{XY}, \overrightarrow{YZ} and \overrightarrow{XZ}:
\overrightarrow{XY}=-\boldsymbol{i}+2\boldsymbol{j}-(2\boldsymbol{i}+3\boldsymbol{j})=-3\boldsymbol{i}-\boldsymbol{j}
\overrightarrow{YZ}=4\boldsymbol{i}-2\boldsymbol{j}-(-\boldsymbol{i}+2\boldsymbol{j})=5\boldsymbol{i}-4\boldsymbol{j}
\overrightarrow{XZ}=4\boldsymbol{i}-2\boldsymbol{j}-(2\boldsymbol{i}+3\boldsymbol{j})=2\boldsymbol{i}-5\boldsymbol{j}
Then, we need to find the magnitudes of those vectors so we can form a triangle:
|\overrightarrow{XY}|=\sqrt{(-3)^2-(-1)^2}=\sqrt{10}
|\overrightarrow{YZ}|=\sqrt{5^2+(-4)^2}=\sqrt{41}
|\overrightarrow{XZ}|=\sqrt{2^2-(-5)^2}=\sqrt{29}
This allows us to draw a triangle:

Finally, using the cosine rule we can calculate the angle \theta:
\cos{\theta}=\dfrac{(\sqrt{29})^2+(\sqrt{41})^2-(\sqrt{10})^2}{2\times\sqrt{29}\times \sqrt{41}}=\dfrac{60}{2\sqrt{1189}}=\dfrac{30}{\sqrt{1189}}\rArr \theta=\cos^{-1}(\dfrac{30}{\sqrt{1189}})=29.54\degree \, (2\text{ dp})
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






