Position Vectors

A LevelAQAEdexcelOCR

Position Vectors Revision

Position Vectors

A position vector describes where a point lies, in relation to the origin, $\boldsymbol{O}$

This allows you to write other vectors in terms of position vectors.

Make sure you are happy with the following topics before continuing.

Vector Basics

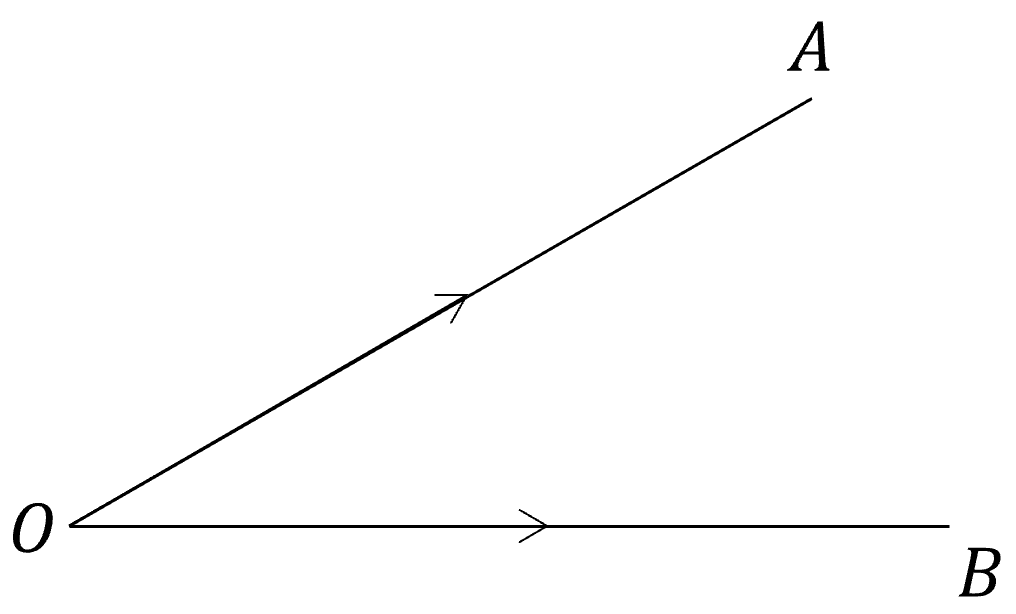
Working with Position Vectors

For a point $A$ , the position vector is denoted as $\overrightarrow{OA}$

Likewise the point $B$ is denoted as $\overrightarrow{OB}$

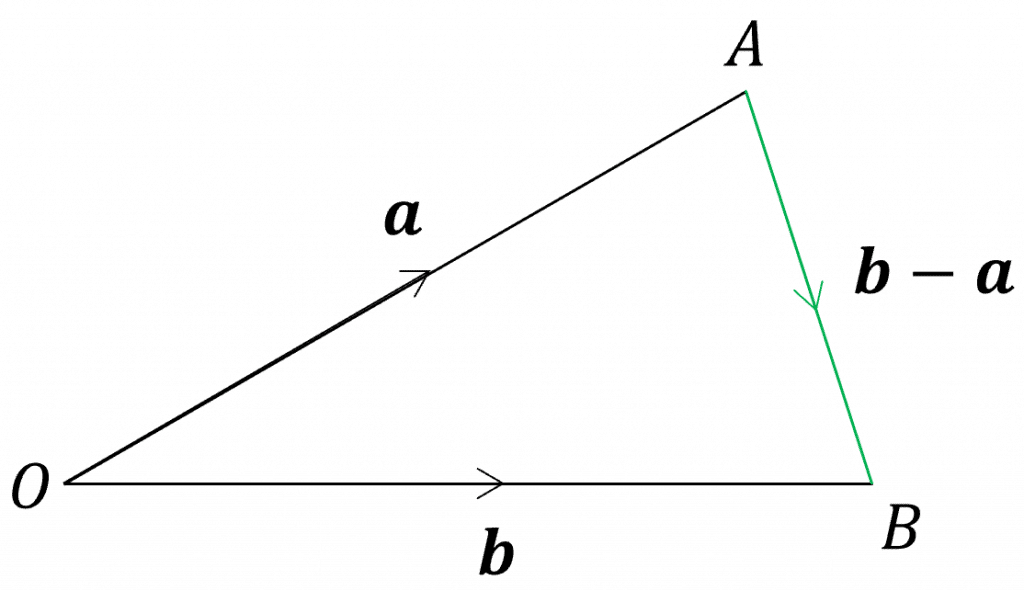
Writing points as position vectors then allows you to describe vectors between points as position vectors.

If we let, $\boldsymbol{a}=\overrightarrow{OA}$ and $\boldsymbol{b}=\overrightarrow{OB}$

Then, $\overrightarrow{AB}=-\overrightarrow{OA}+\overrightarrow{OB}=-\boldsymbol{a}+\boldsymbol{b}=\boldsymbol{b}-\boldsymbol{a}$

Describing vectors using $\boldsymbol{i}$ and $\boldsymbol{j}$ Units

A vector with a magnitude of $1$ unit is called a unit vector
The standard unit vectors are $\boldsymbol{i}$ and $\boldsymbol{j}$ , which are in the direction of the $x$ -axis and $y$ -axis respectively.
These standard unit vectors are used to express the horizontal and vertical position of the end of a vector compared to its start point

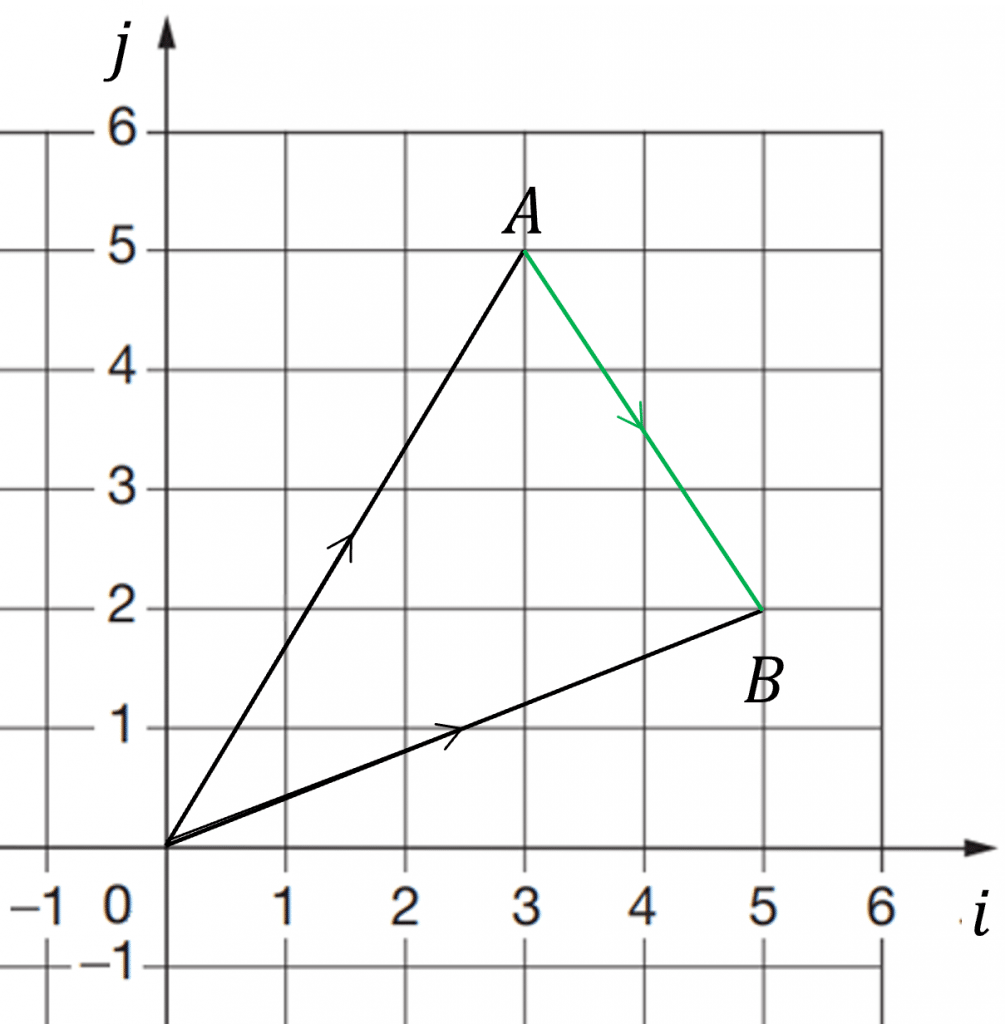
Using the diagram on the right, we can see the position vector of point $A=3\boldsymbol{i}+5\boldsymbol{j}$ and the position vector of point $B=5\boldsymbol{i}+2\boldsymbol{j}$

To write $\overrightarrow{AB}$ in terms of standard unit vectors, we can just add and subtract the $\boldsymbol{i}$ and $\boldsymbol{j}$ components of $\boldsymbol{a}$ and $\boldsymbol{b}$ separately.

Thus the vector $\overrightarrow{AB}=-\boldsymbol{a}+\boldsymbol{b}=-(3\boldsymbol{i}+5\boldsymbol{j})+(5\boldsymbol{i}+2\boldsymbol{j})=2\boldsymbol{i}-3\boldsymbol{j}$

This means that to go from $A$ to $B$ you go $2$ units to the right and $3$ units down.

Column Vectors

Column vectors are another way of expressing vectors.

If $A=4\boldsymbol{i}-3\boldsymbol{j}$ , then the column vector for $A$ is $\dbinom{4}{-3}$

To add and subtract column vectors from one another you simply add or subtract the top row and then add or subtract the bottom row. For example, if $A=\dbinom{5}{-2}$ and $B=\dbinom{1}{3}$ , then $A+B=\dbinom{5+1}{-2+3}=\dbinom{6}{1}$

Multiplying a column vector by a scalar is also straight forward, you just need to multiply both the top and bottom numbers by the scalar. For instance, if $C=\dbinom{-3}{4}$ , $3C=\dbinom{3\times-3}{3\times4}=\dbinom{-9}{12}$

Position Vectors Example Questions

Question 1: Point $K$ has the coordinates $(-1,3)$ .

Give the position vector of point $K$ in:

a) Standard unit vector form

b) Column vector form

[2 marks]

If $A=(x,y)$ , then $A=x\boldsymbol{i}+y\boldsymbol{j}=\dbinom{x}{y}$

So,

a) $K=-\boldsymbol{i}+3\boldsymbol{j}$

b) $K=\dbinom{-1}{3}$

Save your answers with

Gold Standard Education

Question 2: $\boldsymbol{a}$ has a position vector of $\dbinom{7}{-2}$ and $\boldsymbol{b}$ has a position vector of $\dbinom{-3}{-1}$ , what is $2\boldsymbol{a}-4\boldsymbol{b}$ ?

Give your answer as a column vector.

[2 marks]

2\boldsymbol{a}-4\boldsymbol{b}=\dbinom{2\times7}{2\times-2}-\dbinom{4\times-3}{4\times-1}=\dbinom{14}{-4}-\dbinom{-12}{-4}=\dbinom{14-(-12)}{-4-(-4)}=\dbinom{26}{0}

Save your answers with

Gold Standard Education

Question 3: Points $X$ and $Y$ have position vectors $5\boldsymbol{i}-\boldsymbol{j}$ and $-3\boldsymbol{i}+4\boldsymbol{j}$ respectively. Point $Z$ lies on the line $XY$ , such that $XZ:ZY=2:3$ .

Calculate the position vector of $Z$ , giving your answer in standard unit form.

[4 marks]