Vector Basics
Vector Basics Revision
Vector Basics
This section covers what vectors are and how to add them together.
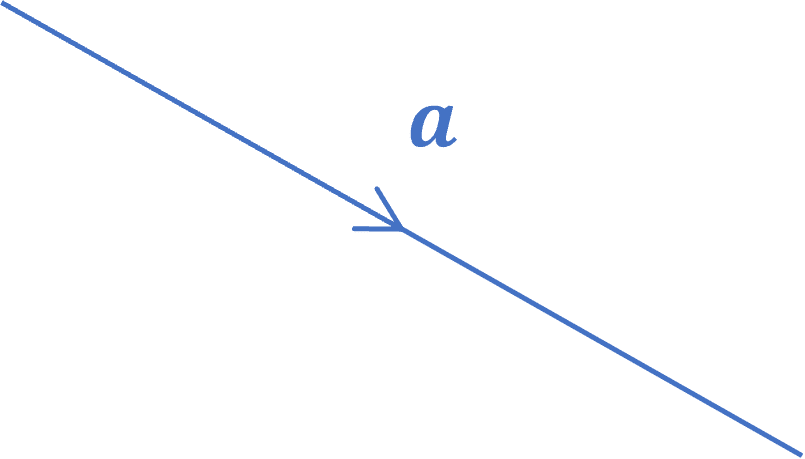

What are Vectors?
A vector contains both size and direction, for example a velocity of 5\text{ m/s} on a bearing of 120\degree
As shown on the right, vectors are drawn as lines with arrowheads on them.
The magnitude (size) of the vector is expressed by the length of the line, these are sometimes drawn to scale.
The direction of the vector is shown by the direction of the arrow.
Note: Vectors represented by a single letter are either written using bold font, \boldsymbol{a}, or with an underline, \underline{a}.
Finding Resultant Vectors
Vectors can be added together by drawing them, then the single vector that goes from the start of the first vector to the end of the final vector is known as the resultant vector.
We can see that to get to the end point of \boldsymbol{r}, we need to go along the vector \boldsymbol{a} then the vector \boldsymbol{b}.
Thus, \boldsymbol{r}=\boldsymbol{a}+\boldsymbol{b}

The order that you add the vectors in doesn’t matter, the resultant vector is always the same.

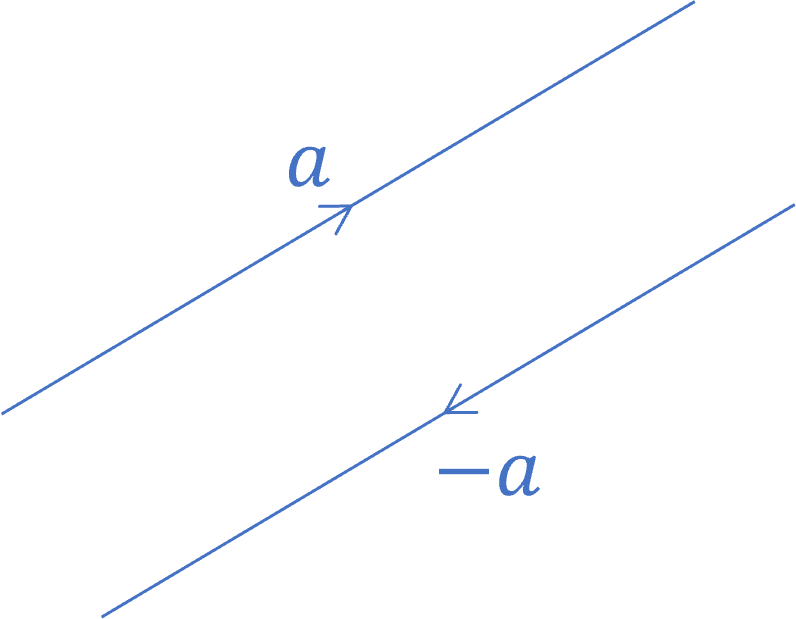

Subtracting Vectors
Subtracting a vector is the same as adding a negative vector.
If \boldsymbol{a} is a vector, then \boldsymbol{-a} is a vector of the same size, in the opposite direction.
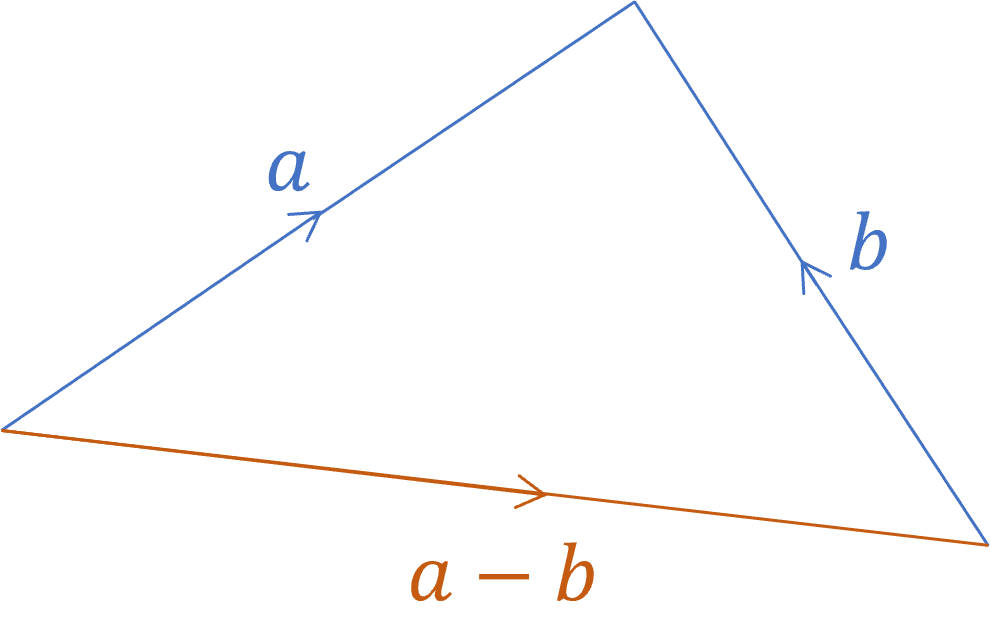

Therefore, subtracting a vector is the same as adding the negative vector.
E.g. \boldsymbol{a-b}=\boldsymbol{a+(-b)}
Multiplying Vectors by Scalars
When you multiply a vector by a scalar (numeric value), this changes the length of the vector, but has no affect on the direction.
If a vector is multiplied by a non-zero scalar, the new vector is always parallel to the original vector, e.g. \boldsymbol{a} is parallel to 3\boldsymbol{a}
To show two vectors are parallel you need to show that they are scalar multiples of each other.
Example: \overrightarrow{AB}=\boldsymbol{x}, \overrightarrow{BC}=\boldsymbol{y}
The point M lies on the line AB and divides \overrightarrow{AB} in the ratio 3:2 and N lies on the line BC and divides \overrightarrow{BC} in the ratio 2:3
Show that \overrightarrow{MN} is parallel to \overrightarrow{AC}
\overrightarrow{AC}=\boldsymbol{x}+\boldsymbol{y}
M divides \overrightarrow{AB} in the ratio 3:2 so M is \dfrac{3}{5} of the way along \overrightarrow{AB}. Therefore, \overrightarrow{AM}=\dfrac{3}{5}\boldsymbol{x}, so \overrightarrow{MB}=\dfrac{2}{5}\boldsymbol{x}.
Similarly, N is \dfrac{2}{5} of the way along \overrightarrow{BC}, so \overrightarrow{BN}=\dfrac{2}{5}\boldsymbol{y}
Finally, \overrightarrow{MN}=\dfrac{2}{5}\boldsymbol{x}+\dfrac{2}{5}\boldsymbol{y}=\dfrac{2}{5}(\boldsymbol{x}+\boldsymbol{y})=\dfrac{2}{5}\overrightarrow{AC}, which shows \overrightarrow{MN} is parallel to \overrightarrow{AC}
Vector Basics Example Questions
Question 1: Find the resultant vector \boldsymbol{r} of the two single vectors \boldsymbol{a} and 2\boldsymbol{b} using the diagram below.

[1 mark]
Going from the start of \boldsymbol{a} to the end of 2\boldsymbol{b}, \boldsymbol{r}=\boldsymbol{a}+2\boldsymbol{b}
Question 2: Using the diagram below, write down the following vectors in terms of \boldsymbol{a},\boldsymbol{b} and \boldsymbol{c}

a) \overrightarrow{XY}
b) \overrightarrow{XZ}
c) \overrightarrow{ZY}
[3 marks]
\overrightarrow{XY}=-\boldsymbol{c}+\boldsymbol{a}
\overrightarrow{XZ}=-\boldsymbol{c}+\boldsymbol{b}
\overrightarrow{ZY}=-\boldsymbol{b}+\boldsymbol{a}
Question 3: \overrightarrow{XY}=\boldsymbol{p}, \overrightarrow{XZ}=\boldsymbol{q}
A divides \overrightarrow{XY} in the ratio 5:1 and B divides \overrightarrow{XZ} in the ratio 5:1
Show that \overrightarrow{YZ} is parallel to \overrightarrow{AB}
[3 marks]
A divides \overrightarrow{XY} in the ratio 5:1 so A is \dfrac{5}{6} of the way along \overrightarrow{XY}. Therefore, \overrightarrow{AX}=-\dfrac{5}{6}\boldsymbol{p}. \\[1.2em]
Similarly, B is \dfrac{5}{6} of the way along \overrightarrow{XZ}, so \overrightarrow{XB}=\dfrac{5}{6}\boldsymbol{q}\\[1.2em]
Finally, \overrightarrow{AB}=-\dfrac{5}{6}\boldsymbol{p}+\dfrac{5}{6}\boldsymbol{q}=\dfrac{5}{6}(-\boldsymbol{p}+\boldsymbol{q})=\dfrac{5}{6}\overrightarrow{YZ}, which shows \overrightarrow{AB} is parallel to \overrightarrow{YZ}
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






