Trig Proofs
Trig Proofs Revision
Trig Proofs
In this section, we’ll be taking a look at some standard proof methods, involving all of the techniques we’ve learned so far.
Example 1
Prove that 1 + \cot ^2 A \equiv \cosec ^2 A.
[3 marks]
1 + \cot ^2 A
= \dfrac{\textcolor{blue}{\sin} ^2 \textcolor{purple}{A}}{\textcolor{blue}{\sin} ^2 \textcolor{purple}{A}} + \dfrac{\textcolor{limegreen}{\cos} ^2 \textcolor{purple}{A}}{\textcolor{blue}{\sin} ^2 \textcolor{purple}{A}}
= \dfrac{\textcolor{blue}{\sin} ^2 \textcolor{purple}{A} + \textcolor{limegreen}{\cos} ^2 \textcolor{purple}{A}}{\textcolor{blue}{\sin} ^2 \textcolor{purple}{A}}
= \dfrac{1}{\textcolor{blue}{\sin} ^2 \textcolor{purple}{A}}
= \cosec ^2 \textcolor{purple}{A}
Example 2
Show that \sqrt{\dfrac{1 - \textcolor{limegreen}{\cos 2x}}{1 + \textcolor{limegreen}{\cos} 2x}} = \textcolor{red}{\tan} x.
[4 marks]
By \textcolor{limegreen}{\cos} 2A \equiv 2\textcolor{limegreen}{\cos} ^2 A - 1 \equiv 1 - 2\textcolor{blue}{\sin} ^2 A,
\sqrt{\dfrac{1 - \textcolor{limegreen}{\cos} 2x}{1 + \textcolor{limegreen}{\cos} 2x}}
= \sqrt{\dfrac{2\textcolor{blue}{\sin} ^2 x}{2\textcolor{limegreen}{\cos} ^2 x}}
= \sqrt{\textcolor{red}{\tan} ^2 x}
= \textcolor{red}{\tan} x
Example 3
Prove that \textcolor{limegreen}{\cos} x = \textcolor{limegreen}{\cos} (-x).
[2 marks]
\textcolor{limegreen}{\cos} (-x)
= \textcolor{limegreen}{\cos} (0 - x)
= \textcolor{limegreen}{\cos} 0 \textcolor{limegreen}{\cos} x + \textcolor{blue}{\sin} 0 \textcolor{blue}{\sin} x
= (1 \times \textcolor{limegreen}{\cos} x) + (0 \times \textcolor{blue}{\sin} x)
= \textcolor{limegreen}{\cos} x
Example 4
Show that \textcolor{red}{\tan} \theta + \cot \theta = 2\cosec 2 \theta.
[3 marks]
\textcolor{red}{\tan} \theta + \cot \theta
= \dfrac{\textcolor{blue}{\sin} \theta}{\textcolor{limegreen}{\cos} \theta} + \dfrac{\textcolor{limegreen}{\cos} \theta}{\textcolor{blue}{\sin} \theta}
= \dfrac{\textcolor{blue}{\sin} ^2 \theta}{\textcolor{blue}{\sin} \theta \textcolor{limegreen}{\cos} \theta} + \dfrac{\textcolor{limegreen}{\cos} ^2 \theta}{\textcolor{blue}{\sin} \theta \textcolor{limegreen}{\cos} \theta}
= \dfrac{\textcolor{blue}{\sin} ^2 \theta + \textcolor{limegreen}{\cos} ^2 \theta}{\textcolor{blue}{\sin} \theta \textcolor{limegreen}{\cos} \theta}
= \dfrac{1}{\textcolor{blue}{\sin} \theta \textcolor{limegreen}{\cos} \theta}
= \dfrac{2}{\textcolor{blue}{\sin} 2\theta}
= 2\cosec 2 \theta
Trig Proofs Example Questions
Question 1: Show that, for small values of x, \dfrac{3 - 3\cos 2x}{4x\tan x} \approx \dfrac{3}{2}.
[3 marks]
\dfrac{3 - 3(1 - 2x^2)}{4x^2} = \dfrac{6x^2}{4x^2} = \dfrac{3}{2}
Question 2: Prove that \dfrac{\sin x}{\cos x} = \tan x.
[2 marks]
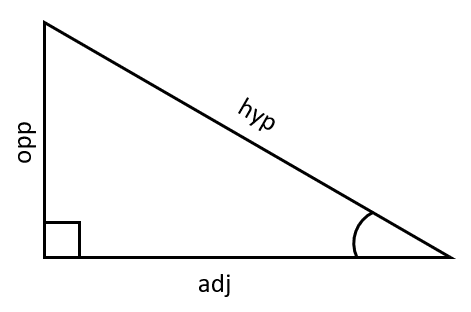
- \sin x = \dfrac{\text{opp}}{\text{hyp}}
- \cos x = \dfrac{\text{adj}}{\text{hyp}}
- \tan x = \dfrac{\text{opp}}{\text{adj}}
\dfrac{\sin x}{\cos x} = \dfrac{\left( \dfrac{\text{opp}}{\text{hyp}}\right) }{\left( \dfrac{\text{adj}}{\text{hyp}}\right) } = \dfrac{\text{opp}}{\text{adj}} = \tan x
Question 3: Show that \cosec ^2 x - \cos ^2 x \equiv \cot ^2 x + \sin ^2 x.
[3 marks]
\begin{aligned}\cot ^2 x + \sin ^2 x&= \dfrac{\cos ^2 x}{\sin ^2 x} + \sin ^2 x\\[1.2em]&= \dfrac{\cos ^2 x}{\sin ^2 x} + 1 - \cos ^2 x\\[1.2em]&= \dfrac{\cos ^2 x}{\sin ^2 x} + \dfrac{\sin ^2 x}{\sin ^2 x} - \cos ^2 x\\[1.2em]&= \dfrac{\cos ^2 x + \sin ^2 x}{\sin ^2 x} - \cos ^2 x\\[1.2em]&=\dfrac{1}{\sin ^2 x} - \cos ^2 x\\[1.2em]&= \cosec ^2 x - \cos ^2 x\end{aligned}
Trig Proofs Worksheet and Example Questions
Trigonometry
A LevelYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






