Exponentials and Logarithms
Exponentials and Logarithms Revision
Exponentials and Logarithms
A sum such as 4+3=7 has two inverses: 7-3=4 and 7-4=3.
A product such as 8\times6=48 has two inverses: 48\div6=8 and 48\div8=6.
An exponential (power) such as 3^{4}=81 has an inverse of the fourth root: \sqrt[4]{81}=3. But for the pattern to continue there must be another inverse – an operation involving 81 and 3 to get back to 4.
This other inverse is the logarithm.
Logarithms are the Inverse of Exponentials
\log_{a}(b)=c means that a^{c}=b
a^{1}=a for any a so \log_{a}(a)=1
a^{0}=1 for any a so \log_{a}(1)=0
Example: \log_{3}(81)=4 because 3^{4}=81
We also have other rules:
\log_{a}(x)+\log_{a}(y)=\log_{a}(xy)
\log_{a}(x)-\log_{a}(y)=\log_{a}\left(\dfrac{x}{y}\right)
\log_{a}(x^{n})=n\log_{a}(x)
\log_{a}(x)=\dfrac{\log_{b}(x)}{\log_{b}(a)}
Note: The little number after the \text{log} is called the base. The most common base is 10, but this is usually left out – i.e. for \text{log}_{10} we just write \text{log} .
Using Logarithms and Exponentials to Solve Equations
We can use the rules above – called the laws of logarithms – to solve equations that involve exponentials.
Example: 3^{4x}=5
\log(3^{4x})=\log(5)
4x\log(3)=\log(5)
\begin{aligned}x&=\dfrac{\log(5)}{4\log(3)}\\[1.2em]&=0.366\end{aligned}
Note: The base of the logarithm was not given in this example. This is because we would get the same answer using any base.
On the flipside, we can use exponentials to solve equations involving logarithms.
Example: 6\log_{4}(x)=17
\log_{4}(x)=\dfrac{17}{6}
\begin{aligned}x&=4^{\frac{17}{6}}\\[1.2em]&=50.8\end{aligned}
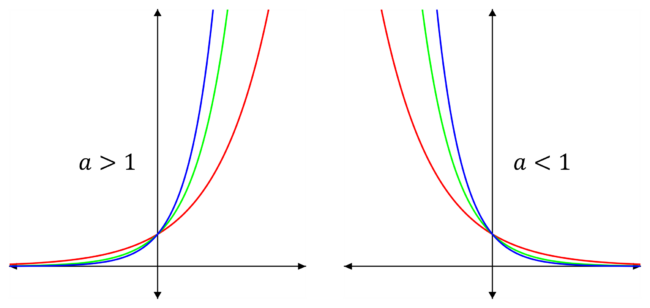
Graphs of Exponentials
An exponential graph is a graph of the function y=a^{x} for some a>0. They all have the same basic shape. If a>1 then y increases as x increases. If a<1 then y decreases as x increases. Larger a gives faster increase if a>1 while smaller a gives faster decrease if a<1.
Note: Exponential graphs never reach \mathbf{0}.
On the left graph is y=2^{x}, y=3^{x} and y=4^{x}.
On the right graph is y=\left(\dfrac{1}{2}\right)^{x}, y=\left(\dfrac{1}{3}\right)^{x} and y=\left(\dfrac{1}{4}\right)^{x}.
Exponentials and Logarithms Example Questions
Question 1: Write the following in logarithm notation:
a) 7^{3}=343
b) 5^{4}=625
c) 2^{16}=65536
d) 729^{\frac{1}{3}}=9
e) 22^{0}=1
[5 marks]
a) \log_{7}(343)=3
b) \log_{5}(625)=4
c) \log_{2}(65536)=16
d) \log_{729}(9)=\dfrac{1}{3}
e) \log_{22}(1)=0
Question 2: Evaluate:
a) \log_{2}(16)
b) \log_{5}(125)
c) \log_{3}(243)
d) \log_{\frac{1}{4}}\left(\dfrac{1}{16}\right)
[4 marks]
a) 4 because 2^{4}=16
b) 3 because 5^{3}=125
c) 5 because 3^{5}=243
d) 2 because \left(\dfrac{1}{4}\right)^{2}=\dfrac{1}{16}
Question 3: Write these expressions as a single logarithm:
a) \log_{a}(12)+\log_{a}(6)
b) 2\log_{b}(5)+\log_{b}(4)
c) 3\log_{6}(2)+\dfrac{1}{2}\log_{6}(9)
[3 marks]
a)
\begin{aligned}\log_{a}(12)+\log_{a}(6)&=\log_{a}(12\times6)\\[1.2em]&=\log_{a}(72)\end{aligned}
b)
\begin{aligned}2\log_{b}(5)+\log_{b}(4)&=\log_{b}(5^{2})+\log_{b}(4)\\[1.2em]&=\log_{b}(25)+\log_{b}(4)\\[1.2em]&=\log_{b}(25\times4)\\[1.2em]&=\log_{b}(100)\end{aligned}
c)
\begin{aligned}3\log_{6}(2)+\dfrac{1}{2}\log_{6}(9)&=\log_{6}(2^{3})+\log_{6}(9^{\frac{1}{2}})\\[1.2em]&=\log_{6}(8)+\log_{6}(3)\\[1.2em]&=\log_{6}(8\times3)\\[1.2em]&=\log_{6}(24)\end{aligned}Question 4: Solve 6^{7x}=38, giving your answer to 3 significant figures.
[2 marks]
6^{7x}=38
7x=\log_{6}(38)
x=\dfrac{1}{7}\log_{6}(38)
x=0.290
Question 5: Solve \log_{6}(x-2)+\log_{6}(x-7)=2
[4 marks]
\log_{6}(x-2)+\log_{6}(x-7)=2
\log_{6}((x-2)(x-7))=2
(x-2)(x-7)=6^{2}
x^{2}-9x+14=36
x^{2}-9x-22=0
(x-11)(x+2)=0
x=11 or x=-2
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






