The Binomial Distribution
The Binomial Distribution Revision
The Binomial Distribution
The Binomial distribution is a distribution that tells us the probability of a certain number of successes given a fixed success probability in repeated trials. To understand what it is and how it works, we first need to understand factorials and binomial coefficients.
Factorial
The factorial of a number, written n! is equal to n\times (n-1)\times (n-2)\times ... \times 3\times 2\times 1
n! is the number of ways you can arrange \bm{n} objects.
You can picture this as having n choices for the first object, n-1 choices for the second object, n-2 choices for the third object, and so on.
What if Some Objects are the Same?
Suppose we are arranging n objects, and r of them are the same. In any given arrangement, we can swap two objects that are the same and end up with the same arrangement. Indeed, if r objects are the same, we can swap them into any order we like within the arrangement and we will not have changed the arrangement. There are r! such ways to swap r objects. So the number of arrangements of n objects, r of which are the same, is \dfrac{n!}{r!}
Only Two Different Objects
Suppose we want to arrange n objects, r of which are of one type and the remaining n-r are of a second type. We can arrange the r identical objects in r! ways and the n-r identical objects in (n-r)! ways. So overall we have \dfrac{n!}{r!(n-r)!} arrangements. This is known as the binomial coefficient of n and r, written as
\begin{pmatrix}n\\r\end{pmatrix}=\text{}^{n}C_{r}=\dfrac{n!}{r!(n-r)!}
A Level Maths Predicted Papers
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A Level Maths Revision Cards
The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. Maths Made Easy is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
The Binomial Distribution
The Binomial distribution tells us the probability of a x successes from n independent events where the probability of success for each event is p.
Its probability function is:
f(x)=\begin{pmatrix}n\\x\end{pmatrix}p^{x}(1-p)^{n-x}
We can understand this as \begin{pmatrix}n\\x\end{pmatrix} is the number of possible ways to have x successes out of n events, then we multiply by the probability of x successes and n-x failures, which is p^{x}(1-p)^{n-x}
Notation: If X is a binomial random variable with n trials and a success probability of p, we write X\sim B(n,p)
Binomial Tables
Your formula booklet may contain binomial tables. These give the cumulative distribution function value for the binomial distribution.
For example, if we want to find the probability of two or less successes out of five trials with a success probability of 0.15:
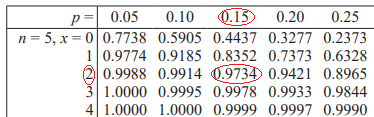
This shows that \mathbb{P}(X\leq 2)=0.9734
If your formula booklet does not have binomial tables, you are expected to use the statistics functions of your calculator to answer questions like this. Make sure you are familiar with how these work, as they will be necessary for an exam.
When to use the Binomial Distribution
A random variable X is binomially distributed if:
- There is a fixed number of trials.
- Each trial has only two outcomes – success or failure.
- The trials are independent of each other.
- The success probability is the same in each trial.
- X is the total number of successes in all trials.
The Binomial Distribution Example Questions
Question 1: Find \begin{pmatrix}6\\3\end{pmatrix}
[2 marks]
\begin{pmatrix}6\\3\end{pmatrix}=
\dfrac{6!}{3!\times 3!}=
\dfrac{6\times 5\times 4\times 3\times 2\times 1}{3\times 2\times 1\times 3\times 2\times 1}=
\dfrac{6\times 5\times 4\times \cancel{3}\times \cancel{2}\times \cancel{1}}{\cancel{3}\times \cancel{2}\times \cancel{1}\times 3\times 2\times 1}=
\dfrac{6\times 5\times 4}{3\times 2\times 1}=
\dfrac{6\times 5\times 4}{6}=
\dfrac{\cancel{6}\times 5\times 4}{\cancel{6}}=
5\times 4=
20
Question 2: What is \mathbb{P}(X=2) if X\sim B(5,0.25)?
[2 marks]
Use the formula:
\mathbb{P}(X=x)=\begin{pmatrix}n\\x\end{pmatrix}p^{x}(1-p)^{n-x}
Here, n=5,p=0.25,x=2
\begin{aligned}\mathbb{P}(X=2)&=\begin{pmatrix}5\\2\end{pmatrix}0.25^{2}(1-0.25)^{5-2}\\[1.2em]&=0.264\end{aligned}
Question 3: For X\sim B(12,0.4), use a binomial table or a calculator to find \mathbb{P}(X\leq 5)
[1 mark]
Question 4: Use a binomial table or a calculator to find \mathbb{P}(3\leq X\leq 6) where X\sim B(8,0.6)
[1 mark]
\mathbb{P}(3\leq X\leq 6)=
\mathbb{P}(X\leq 6)-\mathbb{P}(X\leq 2)
We can use the tables to find these values.
0.8936 - 0.0498 = 0.8438
Question 5: Every time Jeff turns on his television, it goes to a random channel. It can receive 40 channels. Jeff turns on his television 60 times in a month on average. What is the probability that it will show the channel Jeff wants to watch upon turning on at least three times in a month.
[3 marks]
Probability of correct channel is \dfrac{1}{40}, so we have X\sim B(60,\dfrac{1}{40}).
Want to find \mathbb{P}(X\geq 3)
\begin{aligned}\mathbb{P}(X\geq 3)&=1-\mathbb{P}(X\leq 2)\\[1.2em]&=1-0.8105\\[1.2em]&=0.1895\end{aligned}
You May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.