The Normal Distribution

The normal distribution is a bell shaped curve that is symmetric about the mean. It is defined by its mean $\mu$ and its standard deviation $\sigma$ . If $X$ is normally distributed, we write $X\sim N(\mu,\sigma^{2})$ .

Facts About the Normal Distribution

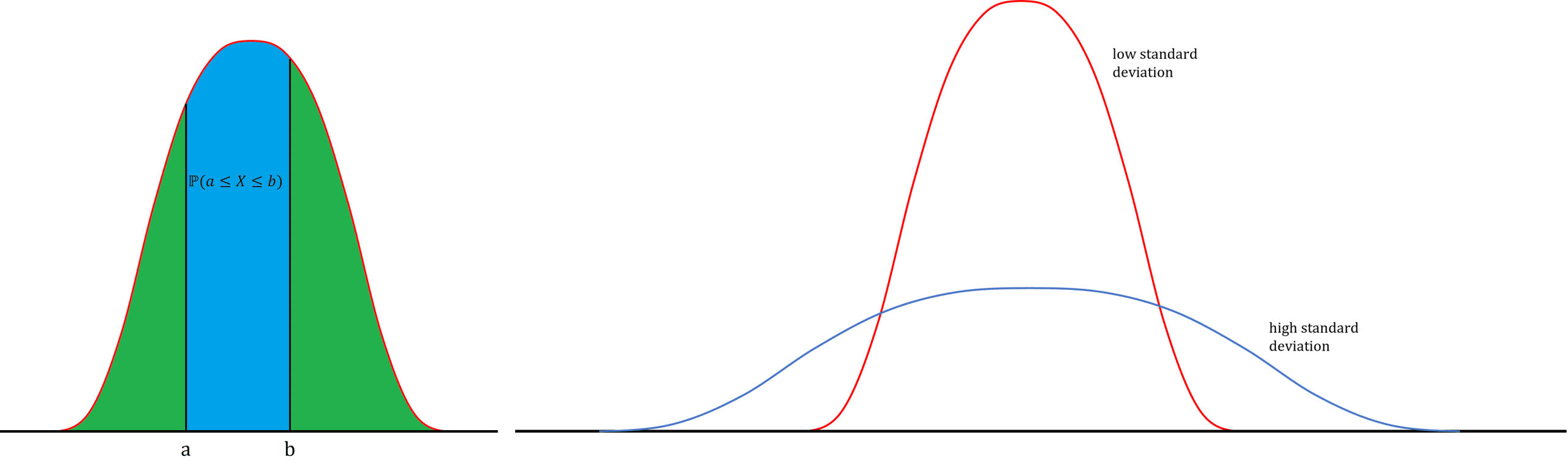
Probability is represented by the area under the graph (note this means the total area under the graph is $1$ ).

The normal distribution is symmetric about the mean $\mu$ , which means:

$\mathbb{P}(X\geq\mu)=\mathbb{P}(X\leq\mu)=0.5$

$\mathbb{P}(X\geq\mu+a)=\mathbb{P}(X\leq\mu-a)\text{ for all }a$

The standard deviation determines how flat the graph is – the higher the standard deviation, the lower the graph.

The graph tends to $0$ as it travels away from the mean, but it never gets there.

Using a Calculator for the Normal Distribution

Your calculator might have a built in function for normal distribution probabilities.

This will ask you to put in a mean and standard deviation and an upper and lower bound on $X$ to produce a probability.

This is fairly straightforward for questions such as $\mathbb{P}(3\leq X\leq 6)$ , but what about questions such as $\mathbb{P}(X\leq 5)$ , where there is no lower bound?

In this case, take the lower bound to be as low as your calculator allows you to input, so that it has as little effect on the result as possible.

Usually, $-9999$ for a lower bound or $9999$ for an upper bound will suffice.

The Inverse Normal Function

Sometimes, you might be given a probability $p$ and asked to find $x$ such that $p=\mathbb{P}(X<x)$ .

For this, we use the inverse normal function, which should also be on your calculator.

You will input a mean, standard deviation and probability and the calculator gives you $x$ such that $p=\mathbb{P}(X<x)$ .

Note: For $<$ and $\leq$ you can do this directly on your calculator. However, for $>$ and $\geq$ you need to subtract $p$ from $1$ to turn $P(X > a)$ into $P(X \leq a) = 1-p$ , then you can use your calculator as normal.

Example: The Normal Distribution

In the $2012$ Olympics Men’s $100$ metre sprint final, the average time taken was $10$ seconds. The times were normally distributed with a variance of $0.2$ seconds. Calculate the probability of a runner having finished the race in $9.58$ seconds or less.

[2 marks]

X\sim N(10,0.2)

Use your calculator, upper bound $9.58$ and lower bound $-9999$

\mathbb{P}(X\leq 9.58)=0.1738

The probability of a runner finishing the race in $9.58$ seconds or less is $0.1738$

The Normal Distribution Example Questions

Question 1: For $X\sim N(4,1)$ , calculate:

a) $\mathbb{P}(X\leq 3.5)$

b) $\mathbb{P}(X\geq 6)$

c) $\mathbb{P}(X\leq 4.25)$

[3 marks]

a) $0.3085$

b) $0.0228$

c) $0.5987$

Save your answers with

Gold Standard Education

Sign Up Now

Question 2: For $X\sim N(75,100)$ , calculate:

a) $\mathbb{P}(90\leq X\leq 110)$

b) $\mathbb{P}(65\leq X\leq 75)$

c) $\mathbb{P}(50\leq X\leq 100)$

[3 marks]

a) $0.0666$

b) $0.3413$

c) $0.9876$

Save your answers with

Gold Standard Education

Sign Up Now

Question 3: For $X\sim N(20,25)$ , find the value of $a$ such that:

a) $\mathbb{P}(X>a)=0.1$

b) $\mathbb{P}(X\leq a)=0.6$

c) $\mathbb{P}(15\leq X\leq a)=0.4$

[4 marks]

a) $a=26.41$

b) $a=21.27$

c) $a=20.74$

Save your answers with

Gold Standard Education

Sign Up Now

Question 4: The weights of punnets of strawberries sold by a greengrocers are $250\text{ g}$ on average with a standard deviation of $9\text{ g}$ . What is the probability that Jenny gets a $280\text{ g}$ punnet or better from the grocers?

[2 marks]

We model this problem with $X\sim N(250,81)$ .

We want to find $\mathbb{P}(X\geq 280)$

$\begin{aligned}\mathbb{P}(X\geq 280)&=1-\mathbb{P}(X\leq 280)\\[1.2em]&=1-\mathbb{P}(X\leq 280)\\[1.2em]&=1-0.9996\\[1.2em]&=0.0004\end{aligned}$

Save your answers with

Gold Standard Education

Sign Up Now