Probability Distributions
Probability Distributions Revision
Probability Distributions
Random variables are variables that take different values with different probabilities. Probability distributions describe their behaviour. The cumulative distribution function is a function formed from the probability distribution, condensing all of the information about a random variable into a useful form.
Random Variables
A random variable, usually denoted with a capital letter such as X, is a variable that takes different values at random with different probabilities. The different values it can take are usually denoted with lowercase letters such as x.
Example: X takes the value of the score on a fair six-sided die. This means that \mathbb{P}(X=1)=\dfrac{1}{6}, \mathbb{P}(X=2)=\dfrac{1}{6}, etc. The possible values for X are x=1,2,3,4,5,6
A discrete random variable can only take a certain number of different values. The example above is a discrete random variable as there are only 6 values X can take.
Probability Distributions and Probability Functions
A probability distribution for a discrete random variable is a table showing all of the possible values for X and their probabilities. The dice example would give:
Note: The probabilities for a random variable must add to 1:
\sum_{x}\mathbb{P}(X=x)=1
We can define the probability function:
f(x)=\mathbb{P}(X=x)
Finally, the cumulative distribution function is a running total of the probability function:
F(x)=\sum_{y\leq x}f(y)=\mathbb{P}(X\leq x)
A Level Maths Predicted Papers 2024
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A Level Maths Revision Cards
The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. MME is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
Example 1: Creating a Probability Distribution
Create a probability distribution for the sum of two dice rolls.
[4 marks]
Step 1: Create a table of every possible outcome. Note that all of these outcomes are equally likely.
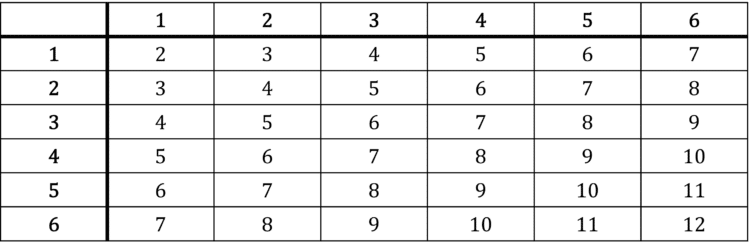
There are thirty-six equally likely outcomes. One of these gives 2, two of these give 3, three of these give 4, four of these give 5, five of these give 6, six of these give 7, five of these give 8, four of these give 9, three of these give 10, two of these give 11 and one of these gives 12. So the probability distribution looks like this:
And after simplifying we have our final answer:
Example 2: Probability Function
From the following probability distribution, determine the probability function and the cumulative distribution function.
[4 marks]
The probability function is defined by f(x)=\mathbb{P}(X=x), so we need a function that satisfies f(1)=0.01, f(2)=0.03, f(3)=0.05, etc. Note that the function increases by 0.02 each time, so is linear with a gradient of 0.02. Hence, we might try f(x)=0.02x+c. Subbing in f(1)=0.01 gives c=-0.01. Hence, the probability function is f(x)=0.02x-0.01
To find the cumulative distribution function, we must first add a running total row to our table.
The cumulative distribution function, F(x), must satisfy F(1)=0.01, F(2)=0.04, F(3)=0.09, etc. This is satisfied by F(x)=\dfrac{x^{2}}{100}.
Probability Distributions Example Questions
Question 1: Create the probability distribution for the number of heads when flipping two coins.
[2 marks]
First create a table of all possibilities.
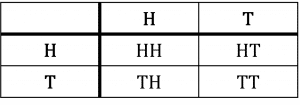
There are 4 equally likely possibilities. One gives 2 heads, two give 1 head and one gives no heads.
Hence, we can construct the probability distribution:
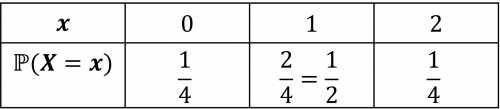
Question 2: From this table, find:
a) The value n
b) \mathbb{P}(2\leq X\leq 4)
[3 marks]
a) Probabilities must add to 1.
0.2+n+0.3+n+0.2=1
2n+0.7=1
2n=0.3
n=0.15
b) \mathbb{P}(2\leq X\leq 4)=
\mathbb{P}(X=2)+\mathbb{P}(X=3)+\mathbb{P}(X=4)=
0.3+0.15+0.2=
0.65
Question 3: A random variable taking values x=1,2,3,4 has probability function f(x)=kx^{2}. Find k.
[4 marks]
First establish the distribution from the probability function.
Now we use the fact that probabilities add to 1:
k+4k+9k+16k=1
30k=1
k=\dfrac{1}{30}
You May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
