Mutually Exclusive Events and Independence
Mutually Exclusive Events and Independence Revision
Mutually Exclusive Events, Independence and Modelling
Mutually exclusive events are events that cannot both happen. Independent events are events that do not affect each other.
Also on this page we will discuss the assumptions made when making a probability model.
Mutually Exclusive Events
Two events \color{red}A and \color{blue}B are mutually exclusive if they can’t both happen – i.e. \mathbb{P}(\color{red}A\color{grey}\cap\color{blue}B\color{grey})=0.
If \color{red}A and \color{blue}B are mutually exclusive, then the probability of \color{red}A or \color{blue}B is the sum of the probabilities of the individual events.
\mathbb{P}(\color{red}A\color{grey}\cup\color{blue}B\color{grey})=\mathbb{P}(\color{red}A\color{grey})+\mathbb{P}(\color{blue}B\color{grey})
Independent Events
If two events \color{red}A and \color{blue}B are independent, then they do not affect each other. This means:
\mathbb{P}(\color{red}A\color{grey}|\color{blue}B\color{grey})=\mathbb{P}(\color{red}A\color{grey})
\mathbb{P}(\color{blue}B\color{grey}|\color{red}A\color{grey})=\mathbb{P}(\color{blue}B\color{grey})
\mathbb{P}(\color{red}A\color{grey}\cap\color{blue}B\color{grey})=\mathbb{P}(\color{red}A\color{grey})\mathbb{P}(\color{blue}B\color{grey})
Modelling Assumptions
Most probability models have made several assumptions in order to be practical to use.
For example, when you roll a die, you assume that each number is equally likely. But in reality, the die could be biased, or could have a small probability of landing on its edge.
Common assumptions include:
- Equally likely events: Are these events actually equally likely? Could there be other low probability outcomes? Are they significant enough to render the model redundant?
- Modelling based on past data: Can we trust the data? How was it sampled? Is it relevant to what we are doing?
- Randomness: Is the outcome genuinely random? Are we doing something that could affect the outcome without us knowing?
Example 1: Mutually Exclusive Events
Events \color{red}A and \color{blue}B are mutually exclusive. If \mathbb{P}(\color{red}A\color{grey}\cup\color{blue}B\color{grey})=0.9 and \mathbb{P}(\color{red}A\color{grey})=0.3, what is the probability of \color{blue}B?
[2 marks]
\mathbb{P}(\color{red}A\color{grey}\cup\color{blue}B\color{grey})=\mathbb{P}(\color{red}A\color{grey})+\mathbb{P}(\color{blue}B\color{grey})
0.9=0.3+\mathbb{P}(\color{blue}B\color{grey})
\begin{aligned}\mathbb{P}(\color{blue}B\color{grey})&=0.9-0.3\\[1.2em]&=0.6\end{aligned}
Example 2: Independent Events
Suppose \mathbb{P}(\color{red}A\color{grey})=0.9, \mathbb{P}(\color{blue}B\color{grey})=0.4 and \mathbb{P}(\color{red}A\color{grey}\cap\color{blue}B\color{grey})=0.3. Are \color{red}A and \color{blue}B independent?
[1 mark]
For independent events, \mathbb{P}(\color{red}A\color{grey})\mathbb{P}(\color{blue}B\color{grey})=\mathbb{P}(\color{red}A\color{grey}\cap\color{blue}B\color{grey})
Here, \mathbb{P}(\color{red}A\color{grey})\mathbb{P}(\color{blue}B\color{grey})=0.9\times 0.4=0.36
And \mathbb{P}(\color{red}A\color{grey}\cap\color{blue}B\color{grey})=0.3
So they are not equal and the events are not independent.
Example 3: Assumptions in Modelling
Define a probability model for flipping a coin twice and state three assumptions you have made.
[5 marks]
We can define the model with a tree diagram:
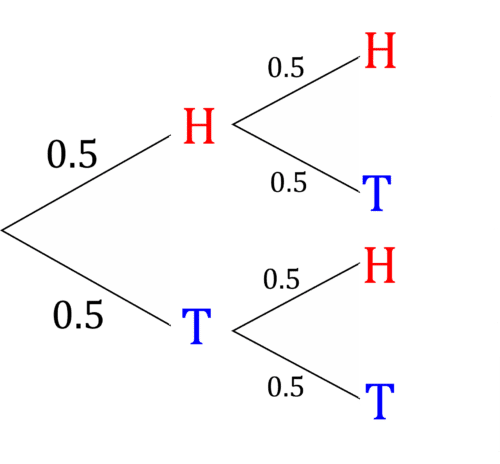
We have assumed that:
- Heads and tails are the only possible outcomes.
- Both outcomes are equally likely.
- The coin tosses are independent.
Mutually Exclusive Events and Independence Example Questions
Question 1: \mathbb{P}(A)=0.35, \mathbb{P}(B)=0.4 and \mathbb{P}(C)=0.3
Is it possible for the events A, B and C to be mutually exclusive?
[2 marks]
If the events are mutually exclusive, then \mathbb{P}(A\cup B\cup C)=\mathbb{P}(A)+\mathbb{P}(B)+\mathbb{P}(C)=0.35+0.4+0.3=1.05 which is a probability greater than 1, which is not allowed. Hence, the events cannot be mutually exclusive.
Question 2: If we assume that rolling a dice and tossing a coin are independent of each other, what is the probability of rolling a 6 then flipping a tails.
[2 marks]
For independent events, to find out the probability of both happening, we just multiply the probabilities of each – remember \mathbb{P}(A\cap B)=\mathbb{P}(A)\mathbb{P}(B)
The probability of rolling a 6 is \dfrac{1}{6} and the probability of flipping a tails is \dfrac{1}{2}
Hence, the probability of both is \dfrac{1}{6}\times\dfrac{1}{2}=\dfrac{1}{12}
Question 3: Previous data indicates that the probability of a train stopping at Harrogate train station in a five minute window is \frac{1}{6}, and that each five minute window is independent of all of the others.
a) What is the probability of two trains arriving in ten minutes?
b) State an assumption you made about the data.
[2 marks]
a) \mathbb{P}(\text{two trains in ten minutes})=\dfrac{1}{6}\times\dfrac{1}{6}=\dfrac{1}{36}
b) We assumed:
- The data is reliable and sampled correctly.
Question 4: For two events A and B, we have \mathbb{P}(A)=0.5, \mathbb{P}(A|B)=0.7 and \mathbb{P}(A\cap B)=0.15.
a) Find:
i) \mathbb{P}(A')
ii) \mathbb{P}(A'|B)
iii) \mathbb{P}(B)
iv) \mathbb{P}(B')
v) \mathbb{P}(A'\cap B)
vi) \mathbb{P}(A\cup B)
b) Are A and B independent?
[8 marks]
a) i)
\begin{aligned}\mathbb{P}(A')&=1-\mathbb{P}(A)\\[1.2em]&=1-0.5\\[1.2em]&=0.5\end{aligned}
ii)
\begin{aligned}\mathbb{P}(A'|B)&=1-\mathbb{P}(A|B)\\[1.2em]&=1-0.7\\[1.2em]&=0.3\end{aligned}
iii)
\begin{aligned}\mathbb{P}(B)&=\dfrac{\mathbb{P}(A\cap B)}{\mathbb{P}(A|B)}\\[1.2em]&=\dfrac{0.15}{0.7}\\[1.2em]&=0.214\end{aligned}
iv)
\begin{aligned}\mathbb{P}(B')&=1-\mathbb{P}(B)\\[1.2em]&=1-0.214\\[1.2em]&=0.786\end{aligned}
v) \mathbb{P}(B)=\mathbb{P}(A\cap B)+\mathbb{P}(A'\cap B)
0.214=0.15+\mathbb{P}(A'\cap B)
\begin{aligned}\mathbb{P}(A'\cap B)&=0.214-0.15\\[1.2em]&=0.064\end{aligned}
vi)
\begin{aligned}\mathbb{P}(A\cup B)&=\mathbb{P}(A)+\mathbb{P}(B)-\mathbb{P}(A\cap B)\\[1.2em]&=0.5+0.214-0.15\\[1.2em]&=0.564\end{aligned}
b) If A and B are independent, then \mathbb{P}(A)\mathbb{P}(B)=\mathbb{P}(A\cap B).
\mathbb{P}(A)\mathbb{P}(B)=0.5\times 0.214=0.107
\mathbb{P}(A\cap B)=0.15
So they are not equal, so the events are not independent.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.






