Parametric Equations
Parametric Equations Revision
Parametric Equations
So far we have seen graphs from Cartesian equations – this is where a single equation that links x and y defines a graph.
Sometimes, for graphs that are more complicated, it is easier to have two equations, one for x and one for y, that are linked by a shared parameter. This is a parametric equation.
There are six skills you need to know for parametric equations.
Make sure you are happy with the following topics before continuing.
Skill 1: Parametric Equations
You need to understand what parametric equations mean and how to plot graphs from them.
Example: Sketch the graph of x=t-1 and y=t^{2}.
Create a table of points:

Now plot these points on a graph.
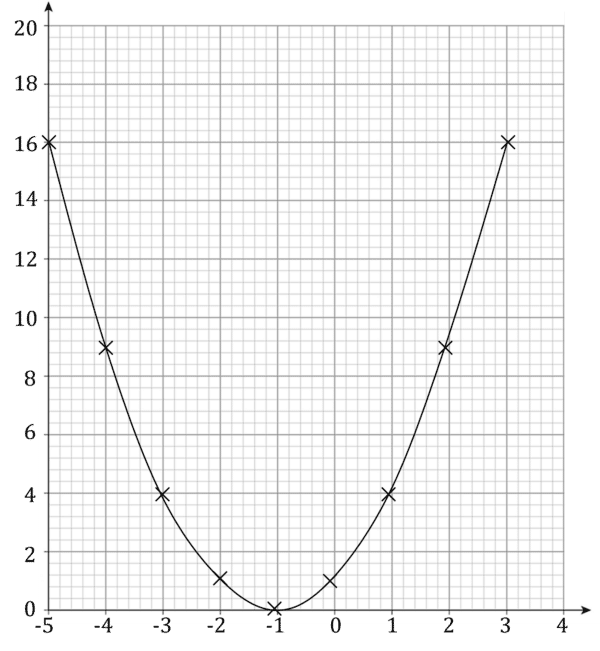
You should also be able to answer questions such as “what is the value of y when t=4” and “what value of t corresponds to y=1”. All questions of this form can be solved by substituting in the right values into the parametric equation.
Example: For the graph x=t-1 and y=t^{2}, find the value of y when x=5.
x=t-1
5=t-1
t=6
\begin{aligned}y&=t^{2}\\[1.2em]&=6^{2}\\[1.2em]&=36\end{aligned}

Skill 2: Parametric Equations of Circles
While t is the most common parameter, some parametric equations use trigonometric functions, so use the parameter \theta.
The parametric equation of a circle with radius r and centre (a,b) is:
x=r\cos(\theta)+a
y=r\sin(\theta)+b
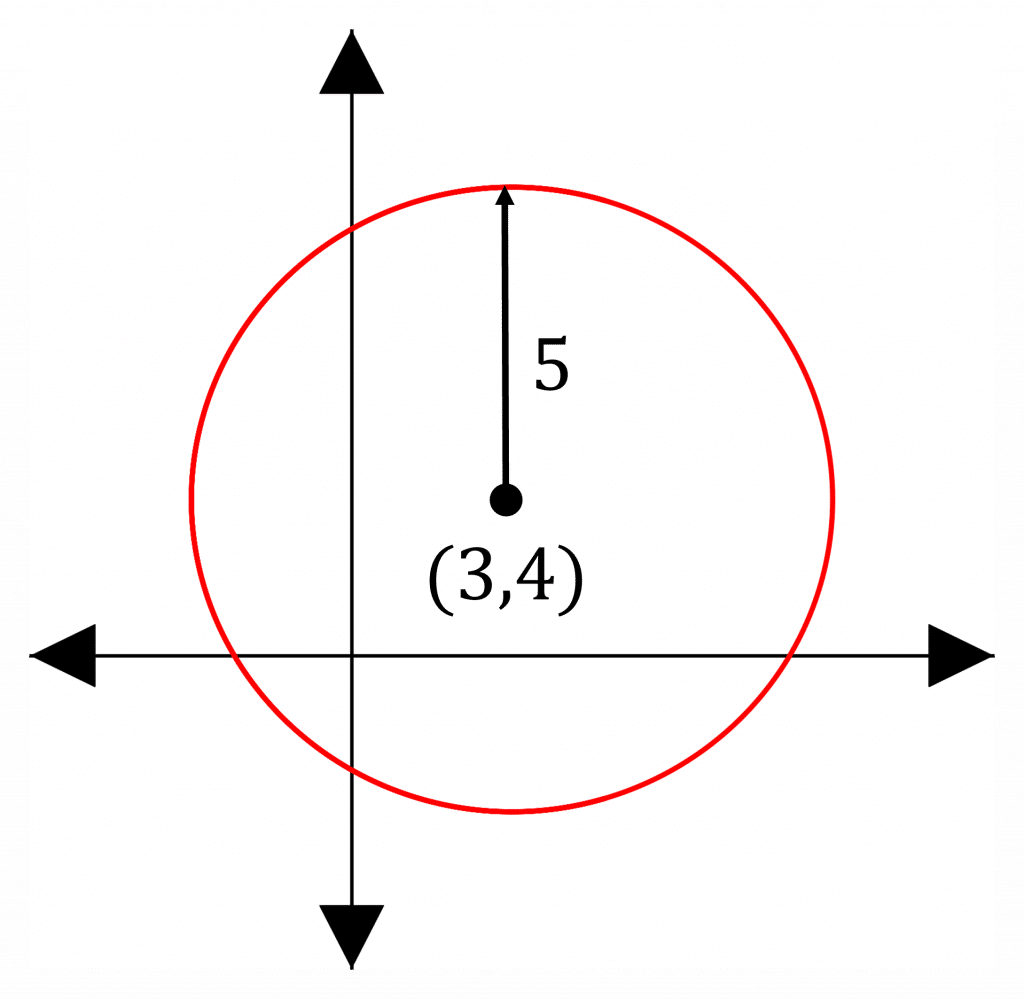
Example: The picture on the right shows a circle with centre (3,4) and radius 5.
It has cartesian equation (x-3)^{2}+(y-4)^{2}=25
It has parametric equation x=5\cos(\theta)+3 and y=5\sin(\theta)+4.
Note: If the radius were different in the x equation and the y equation then we would have an ellipse.
Skill 3: Intersections of Graphs and Parametric Equations
To find the intersection of a parametric equation and Cartesian equation on a graph, substitute in the values for t for x and y into the Cartesian equation, then solve for t, then find the x and y values corresponding to that value of t.
Example: Find where the graph x=3t+4 and y=2t^{2} intersects the line y=x+1
y=x+1Substitute in expressions in t
2t^{2}=3t+4+1
2t^{2}=3t+5
2t^{2}-3t-5=0
(2t-5)(t+1)=0
t=\dfrac{5}{2} or t=-1
x=3t+4x=3\times\dfrac{5}{2}+4 or x=3\times(-1)+4
x=\dfrac{15}{2}+4 or x=-3+4
x=\dfrac{23}{2} or x=1
y=x+1When x = \dfrac{23}{2}, y=\dfrac{23}{2}+1 = \dfrac{25}{2}
When x = 1, y=1+1 = 2
Skill 4: Finding the Cartesian Equation
It is possible to get back to the cartesian equation of a graph from its parametric form. The way to do this is to rearrange the equation of one of x or y into the format t=f(x) or t=f(y), then substitute in this expression for t into the other equation.
Example: Find the Cartesian equation of y=t^{2}, x=t+5
x=t+5
t=x-5
\begin{aligned}y&=t^{2}\\[1.2em]&=(x-5)^{2}\end{aligned}
Skill 5: Using Trig Identities to find the Cartesian Equation
Note: For more about trig identities, go to the Trigonometric Identities page.
For parametric equations involving \theta and trigonometric functions, it is often necessary to use trig identities to recover the cartesian form.
Example: Find the Cartesian equation of x=1+cos(\theta), y=cos(2\theta)
x=1+cos(\theta)
cos(\theta)=x-1
\begin{aligned}y&=cos(2\theta)\\[1.2em]&=2cos^{2}(\theta)-1\\[1.2em]&=2(x-1)^{2}-1\\[1.2em]&=2(x^{2}-2x+1)-1\\[1.2em]&=2x^{2}-4x+2-1\\[1.2em]&=2x^{2}-4x+1\end{aligned}
Skill 6: Modelling with Parametric Equations
Parametric equations can be used to model real life situations. However, this can place restrictions on the parameter because some scenarios are not possible in real life.
- The equations could model for a parameter where only some x and y values make sense, e.g. positive values.
- Restrictions could exist to avoid repeating values of x and y, such as limiting \theta to 0<\theta<2\pi.
- Avoiding dividing by zero is another reason for restrictions, for example if we had x=\dfrac{1}{t-1} we must say t\neq 1.
The values of the parameter that are allowed are collectively called the domain of the parameter.
Example: A tennis ball is thrown into the air. Its horizontal distance from the point of throwing is x=25t, and its vertical distance from the point of throwing is y=9t-t^{2}. Find its vertical distance when it has travelled 50m horizontally.
We can approach this problem in the same way we would approach a problem that is not modelling a real thing.
\begin{aligned}x&=25t\\[1.2em]&=50\end{aligned}
25t=50
t=2
\begin{aligned}y&=9t-t^{2}\\[1.2em]&=9\times2-2^{2}\\[1.2em]&=18-4\\[1.2em]&=14\text{ m}\end{aligned}
Parametric Equations Example Questions
Question 1: Consider the parametric equation x=2t+1, y=t^{2}+3t
a) Find x and y when t=3.
b) What is the value of t when x=4?
c) What is the value of y when x=5?
[4 marks]
a)
\begin{aligned}x&=2t+1\\[1.2em]&=2\times3+1\\[1.2em]&=6+1\\[1.2em]&=7\end{aligned}
\begin{aligned}y&=t^{2}+3t\\[1.2em]&=3^{2}+3\times3\\[1.2em]&=9+9\\[1.2em]&=18\end{aligned}
b) x=2t+1
4=2t+1
2t=3
t=\dfrac{3}{2}
c) x=2t+1
5=2t+1
2t=4
t=2
\begin{aligned}y&=t^{2}+3t\\[1.2em]&=2^{2}+3\times2\\[1.2em]&=4+6\\[1.2em]&=10\end{aligned}
Question 2: State the centre and radius of the circles from these parametric equations:
a) x=2\cos(\theta)+1
y=2\sin(\theta)-1
b) x=5\cos(\theta)+2
y=5\sin(\theta)+5
c) x=16\cos(\theta)-12
y=16\sin(\theta)-13[3 marks]
a) Centre: (1,-1)
Radius: 2
b) Centre: (2,5)
Radius: 5
c) Centre: (-12,-13)
Radius: 16
Question 3: Where does the line y=8x+3 intersect the graph x=3t+1 and y=t^{2}+17t+3?
[4 marks]
y=8x+3
x=3t+1
y=t^{2}+17t+3
\begin{aligned}t^{2}+17t+3&=8(3t+1)+3\\[1.2em]&=24t+8+3\\[1.2em]&=24t+11\end{aligned}
t^{2}-7t-8=0
(t-8)(t+1)=0
t=8 or t=-1
x=3t+1
x=3\times8+1 or x=3\times(-1)+1
x=24+1 or x=-3+1
x=25 or x=-2
y=8x+3
When x = 25, y=8\times25+3 = 200+3 = 203
When x=-2, y=8\times(-2)+3 = -16 + 3 = -13
Question 4: Find the Cartesian equation of the parametric equation:
y=t^{3}+3t^{2}+6t+9
x=\dfrac{1}{2}t-3
[3 marks]
x=\dfrac{1}{2}t-3
2x=t-6
t=2x+6
\begin{aligned}y&=t^{3}+3t^{2}+6t+9\\[1.2em]&=(2x+6)^{3}+3(2x+6)^{2}+6(2x+6)+9\\[1.2em]&=8x^{3}+72x^{2}+216x+216+3(4x^{2}+24x+36)\\[1.2em]&+12x+36+9\\[1.2em]&=8x^{3}+72x^{2}+216x+216+12x^{2}+72x+108\\[1.2em]&+12x+36+9\\[1.2em]&=8x^{3}+84x^{2}+300x+369\end{aligned}
Question 5: Find the Cartesian equation of the parametric equation:
x=\sin(2\theta)
y=\sin^{2}(\theta)\cos^{2}(\theta)
[2 marks]
\dfrac{x}{2}=\sin(\theta)\cos(\theta)
\begin{aligned}y&=\sin^{2}(\theta)\cos^{2}(\theta)\\[1.2em]&=(\sin(\theta)\cos(\theta))^{2}\\[1.2em]&=(\dfrac{x}{2})^{2}\\[1.2em]&=\dfrac{x^{2}}{4}\end{aligned}
Question 6: A kite flies through the air according to the parametric equation:
x=25t+4y=8t-t^{2}
where x is horizontal distance and y is vertical distance.
How far has the kite travelled horizontally when it hits the ground.
[3 marks]
Hitting ground is y=0.
y=8t-t^{2}
8t-t^{2}=0
t(8-t)=0
t=0 or t=8
t=0 is the start, so the solution we want is t=8.
\begin{aligned}x&=25t+4\\[1.2em]&=25\times8+4\\[1.2em]&=200+4\\[1.2em]&=204\end{aligned}