Revise
Circumcircles
Circumcircles Revision
Circumcircles
(Note: This topic is Edexcel only.)
Circumcircles are circles that touch all three points of a triangle. To find a triangle’s circumcircle combines all of the skills of geometry, including circle theorems, perpendicular bisectors, midpoints, lengths and finally forming the equation of a circle.
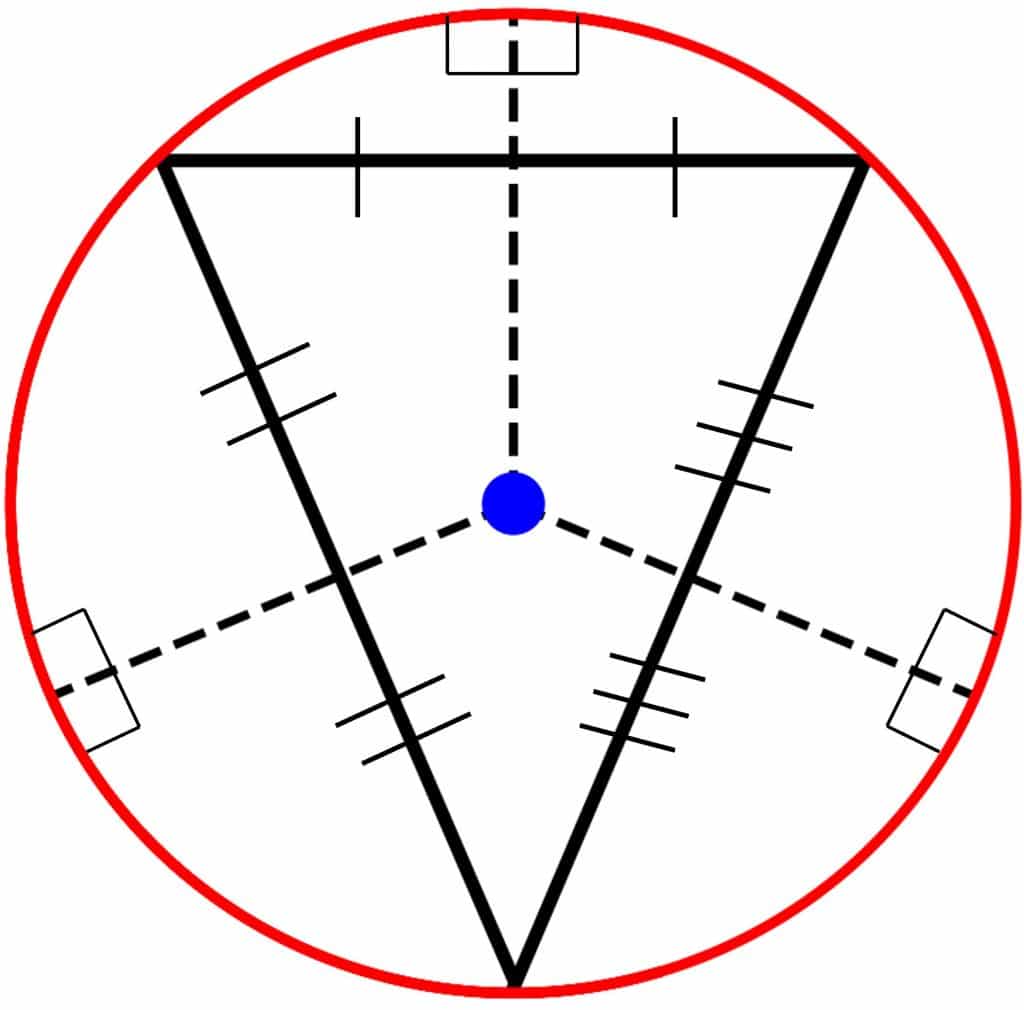
The Circumcircle
A circumcircle is a circle that passes through all three vertices of a triangle. You may need to find the equation of a circumcircle given the three points of a triangle.
Notice that the perpendicular bisectors of the sides of the triangle all meet at the centre – this is because the perpendicular from the centre to a chord bisects the chord, and all of the sides of the triangle are chords.
This means that, to find the centre of the circle, simply find two of the perpendicular bisectors of the sides of the triangle, and find where they intersect.
Then, the radius is simply the distance from the centre to one of the corners of the triangle.
Example: Equation of a Circumcircle
A triangle has vertices (1,1),(2,3),(0,5). Find the equation of its circumcircle.
[8 marks]
Step 1: Find equation of the perpendicular bisector of the line through (1,1) and (2,3).
\begin{aligned}\text{gradient}&=\dfrac{3-1}{2-1}\\[1.2em]&=\dfrac{2}{1}\\[1.2em]&=2\end{aligned}
So gradient of perpendicular bisector is \dfrac{-1}{2}
\begin{aligned}\text{m.point}&=\left(\dfrac{1+2}{2},\dfrac{1+3}{2}\right)\\[1.2em]&=\left(\dfrac{3}{2},\dfrac{4}{2}\right)\\[1.2em]&=\left(\dfrac{3}{2},2\right)\end{aligned}
So the perpendicular bisector goes through the point \left(\dfrac{3}{2},2\right)
Now use all of this information to generate the equation of a line in the form y=mx+c:
y-y_{1}=m(x-x_{1})
y-2=\dfrac{-1}{2}(x-\dfrac{3}{2})
y-2=-\dfrac{1}{2}x+\dfrac{3}{4}
y=-\dfrac{1}{2}x+\dfrac{3}{4}+2
y=-\dfrac{1}{2}x+\dfrac{11}{4}
Step 2: Find equation of the perpendicular bisector of the line through (2,3) and (0,5).
\begin{aligned}\text{gradient}&=\dfrac{5-3}{0-2}\\[1.2em]&=\dfrac{2}{-2}\\[1.2em]&=-1\end{aligned}
So gradient of perpendicular bisector is 1
\begin{aligned}\text{m.point}&=\left(\dfrac{2+0}{2},\dfrac{3+5}{2}\right)\\[1.2em]&=\left(\dfrac{2}{2},\dfrac{8}{2}\right)\\[1.2em]&=(1,4)\end{aligned}
So the perpendicular bisector goes through the point (1,4)
Now use all of this information to generate the equation of a line in the form y=mx+c:
y-y_{1}=m(x-x_{1})
y-4=x-1
y=x-1+4
y=x+3
Step 3: Find centre by finding where the perpendicular bisectors intersect.
y=-\dfrac{1}{2}x+\dfrac{11}{4}
y=x+3
x+3=-\dfrac{1}{2}x+\dfrac{11}{4}
\dfrac{3}{2}x+3=\dfrac{11}{4}
\dfrac{3}{2}x=\dfrac{11}{4}-3
\dfrac{3}{2}x=-\dfrac{1}{4}
x=-\dfrac{2}{3}\times\dfrac{1}{4}
x=-\dfrac{2}{12}
x=\dfrac{-1}{6}
y=x+3
y=-\dfrac{1}{6}+3
y=\dfrac{17}{6}
So centre is \left(\dfrac{-1}{6},\dfrac{17}{6}\right)
Step 4: Find the radius of the circumcircle by finding the distance from one corner to the centre.
Here we use corner (1,1).
\begin{aligned}\text{r}&=\sqrt{\left(\dfrac{-1}{6}-1\right)^{2}+\left(\dfrac{17}{6}-1\right)^{2}}\\[1.2em]&=\sqrt{\left(\dfrac{-7}{6}\right)^{2}+\left(\dfrac{11}{6}\right)^{2}}\\[1.2em]&=\sqrt{\dfrac{49}{36}+\dfrac{121}{36}}\\[1.2em]&=\sqrt{\dfrac{170}{36}}\\[1.2em]&=\sqrt{\dfrac{85}{18}}\\[1.2em]&=\dfrac{\sqrt{170}}{6}\end{aligned}
Step 5: Put it all together in an equation.
\left(x-\dfrac{-1}{6}\right)^{2}+\left(y-\dfrac{17}{6}\right)^{2}=\left(\dfrac{\sqrt{170}}{6}\right)^{2}
\left(x+\dfrac{1}{6}\right)^{2}+\left(y-\dfrac{17}{6}\right)^{2}=\dfrac{170}{36}
Circumcircles Example Questions
Question 1: Find the perpendicular bisectors of the edges of the triangle that has vertices at (-1,-1),(-3,-5),(-6,2), in the form y=mx+c
[6 marks]
Side (-1,-1),(-3,-5):
\begin{aligned}\text{gradient}&=\dfrac{-5-(-1)}{-3-(-1)}\\[1.2em]&=\dfrac{-4}{-2}\\[1.2em]&=2\end{aligned}
So the gradient of the perpendicular bisector is \dfrac{-1}{2}
\begin{aligned}\text{midpoint}&=\left(\dfrac{-1-3}{2},\dfrac{-1-5}{2}\right)\\[1.2em]&=\left(\dfrac{-4}{2},\dfrac{-6}{2}\right)\\[1.2em]&=(-2,-3)\end{aligned}
So the perpendicular bisector passes through the point (-2,-3)
Now use all of this information to generate an equation in the form y=mx+c
y-y_{1}=m(x-x_{1})
y-(-3)=\dfrac{-1}{2}(x-(-2))
y+3=-\dfrac{1}{2}(x+2)
y+3=-\dfrac{1}{2}x-1
y=-\dfrac{1}{2}x-4
Side (-1,-1),(-6,2):
\begin{aligned}\text{gradient}&=\dfrac{2-(-1)}{-6-(-1)}\\[1.2em]&=\dfrac{3}{-5}\\[1.2em]&=-\dfrac{3}{5}\end{aligned}
So the gradient of the perpendicular bisector is \dfrac{5}{3}
\begin{aligned}\text{midpoint}&=\left(\dfrac{-1-6}{2},\dfrac{-1+2}{2}\right)\\[1.2em]&=\left(\dfrac{-7}{2},\dfrac{1}{2}\right)\end{aligned}
So the perpendicular bisector passes through the point \left(\dfrac{-7}{2},\dfrac{1}{2}\right)
Now use all of this information to generate an equation in the form y=mx+c
y-y_{1}=m(x-x_{1})
y-\dfrac{1}{2}=\dfrac{5}{3}(x-\dfrac{-7}{2})
y-\dfrac{1}{2}=\dfrac{5}{3}(x+\dfrac{7}{2})
y-\dfrac{1}{2}=\dfrac{5}{3}x+\dfrac{35}{6}
y=\dfrac{5}{3}x+\dfrac{19}{3}
Side (-3,-5),(-6,2):
\begin{aligned}\text{gradient}&=\dfrac{2-(-5)}{-6-(-3)}\\[1.2em]&=\dfrac{7}{-3}\\[1.2em]&=-\dfrac{7}{3}\end{aligned}
So the gradient of the perpendicular bisector is \dfrac{3}{7}
\begin{aligned}\text{midpoint}&=\left(\dfrac{-3-6}{2},\dfrac{-5+2}{2}\right)\\[1.2em]&=\left(\dfrac{-9}{2},\dfrac{-3}{2}\right)\end{aligned}
So the perpendicular bisector passes through the point \left(\dfrac{-9}{2},\dfrac{-3}{2}\right)
Now use all of this information to generate an equation in the form y=mx+c
y-y_{1}=m(x-x_{1})
y-\dfrac{-9}{2}=\dfrac{3}{7}(x-\dfrac{-3}{2})
y+\dfrac{9}{2}=\dfrac{3}{7}(x+\dfrac{3}{2})
y+\dfrac{9}{2}=\dfrac{3}{7}x+\dfrac{9}{14}
y=\dfrac{3}{7}x-\dfrac{27}{7}
Question 2: The three perpendicular bisectors of a triangle are:
y=3x+1
y=-\dfrac{1}{3}x-\dfrac{17}{3}
y=-4x-13
Find the centre of the circumcircle of the triangle.
[3 marks]
Centre of circumcircle is where all three lines intersect.
3x+1=-4x-13
7x=-14
x=-2
y=3x+1
y=3(-2)+1
y=-6+1
y=-5
Check this works with the other perpendicular bisector:
y=-\dfrac{1}{3}(-2)-\dfrac{17}{3}
y=\dfrac{2}{3}-\dfrac{17}{3}
y=\dfrac{-15}{3}
y=-5
So all three perpendicular bisectors intersect at (-2,-5)
Question 3: A triangle has vertices (-1,2),(3,5),(4,4). Find the equation of its circumcircle.
[8 marks]
Find equation of the perpendicular bisector of the line through (-1,2) and (3,5).
\begin{aligned}\text{gradient}&=\dfrac{5-2}{3-(-1)}\\[1.2em]&=\dfrac{3}{3+1}\\[1.2em]&=\dfrac{3}{4}\end{aligned}
So gradient of perpendicular bisector is \dfrac{-4}{3}
\begin{aligned}\text{midpoint}&=\left(\dfrac{-1+3}{2},\dfrac{2+5}{2}\right)\\[1.2em]&=\left(\dfrac{2}{2},\dfrac{7}{2}\right)\\[1.2em]&=\left(1,\dfrac{7}{2}\right)\end{aligned}
So the perpendicular bisector goes through the point \left(1,\dfrac{7}{2}\right)
Now use all of this information to generate the equation of a line in the form y=mx+c:
y-y_{1}=m(x-x_{1})
y-\dfrac{7}{2}=\dfrac{-4}{3}(x-1)
y-\dfrac{7}{2}=-\dfrac{4}{3}x+\dfrac{4}{3}
y=-\dfrac{4}{3}x+\dfrac{4}{3}+\dfrac{7}{2}
y=-\dfrac{4}{3}x+\dfrac{29}{6}
Find equation of the perpendicular bisector of the line through (3,5) and (4,4).
\begin{aligned}\text{gradient}&=\dfrac{5-4}{3-4}\\[1.2em]&=\dfrac{1}{-1}\\[1.2em]&=-1\end{aligned}
So gradient of perpendicular bisector is 1
\begin{aligned}\text{midpoint}&=\left(\dfrac{3+4}{2},\dfrac{5+4}{2}\right)\\[1.2em]&=\left(\dfrac{7}{2},\dfrac{9}{2}\right)\end{aligned}
So the perpendicular bisector goes through the point \left(\dfrac{7}{2},\dfrac{9}{2}\right)
Now use all of this information to generate the equation of a line in the form y=mx+c:
y-y_{1}=m(x-x_{1})
y-\dfrac{9}{2}=x-\dfrac{7}{2}
y=x-\dfrac{7}{2}+\dfrac{9}{2}
y=x+1
Find centre by finding where the perpendicular bisectors intersect.
y=-\dfrac{4}{3}x+\dfrac{29}{6}
y=x+1
x+1=-\dfrac{4}{3}x+\dfrac{29}{6}
\dfrac{7}{3}x+1=\dfrac{29}{6}
\dfrac{7}{3}x=\dfrac{29}{6}-1
\dfrac{7}{3}x=\dfrac{23}{6}
x=\dfrac{3}{7}\times\dfrac{23}{6}
x=\dfrac{69}{42}
x=\dfrac{23}{14}
y=x+1
y=\dfrac{23}{14}+1
y=\dfrac{37}{14}
So centre is \left(\dfrac{23}{14},\dfrac{37}{14}\right)
Find the radius of the circumcircle by finding the distance from one corner to the centre.
Here we use corner (4,4).
\begin{aligned}\text{r}&=\sqrt{\left(\dfrac{23}{14}-4\right)^{2}+\left(\dfrac{37}{14}-4\right)^{2}}\\[1.2em]&=\sqrt{\left(\dfrac{-33}{14}\right)^{2}+\left(\dfrac{-19}{14}\right)^{2}}\\[1.2em]&=\sqrt{\dfrac{1089}{196}+\dfrac{361}{196}}\\[1.2em]&=\sqrt{\dfrac{1450}{196}}\\[1.2em]&=\sqrt{\dfrac{725}{98}}\\[1.2em]&=\dfrac{5\sqrt{58}}{14}\end{aligned}
Put it all together in an equation.
\left(x-\dfrac{23}{14}\right)^{2}+\left(y-\dfrac{37}{14}\right)^{2}=\left(\dfrac{5\sqrt{58}}{14}\right)^{2}
\left(x-\dfrac{23}{14}\right)^{2}+\left(y-\dfrac{37}{14}\right)^{2}=\dfrac{725}{98}
