Revise
Circle Geometry
Circle Geometry Revision
Circle Geometry
Circles, like lines, have their own equations on graphs. However, circle equations are a little different, and the geometry a little more in-depth.
A Level Maths Predicted Papers 2025
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A-A* A Level Maths Practice Papers
The MME A-A* A level maths practice papers are excellent for those top achieving students to practise for their exams, using authentic exam style questions that are unique to our practice papers. Our content experts have studied A level maths past papers and specifications to develop specific A-A* A level maths exam questions in an authentic exam style. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
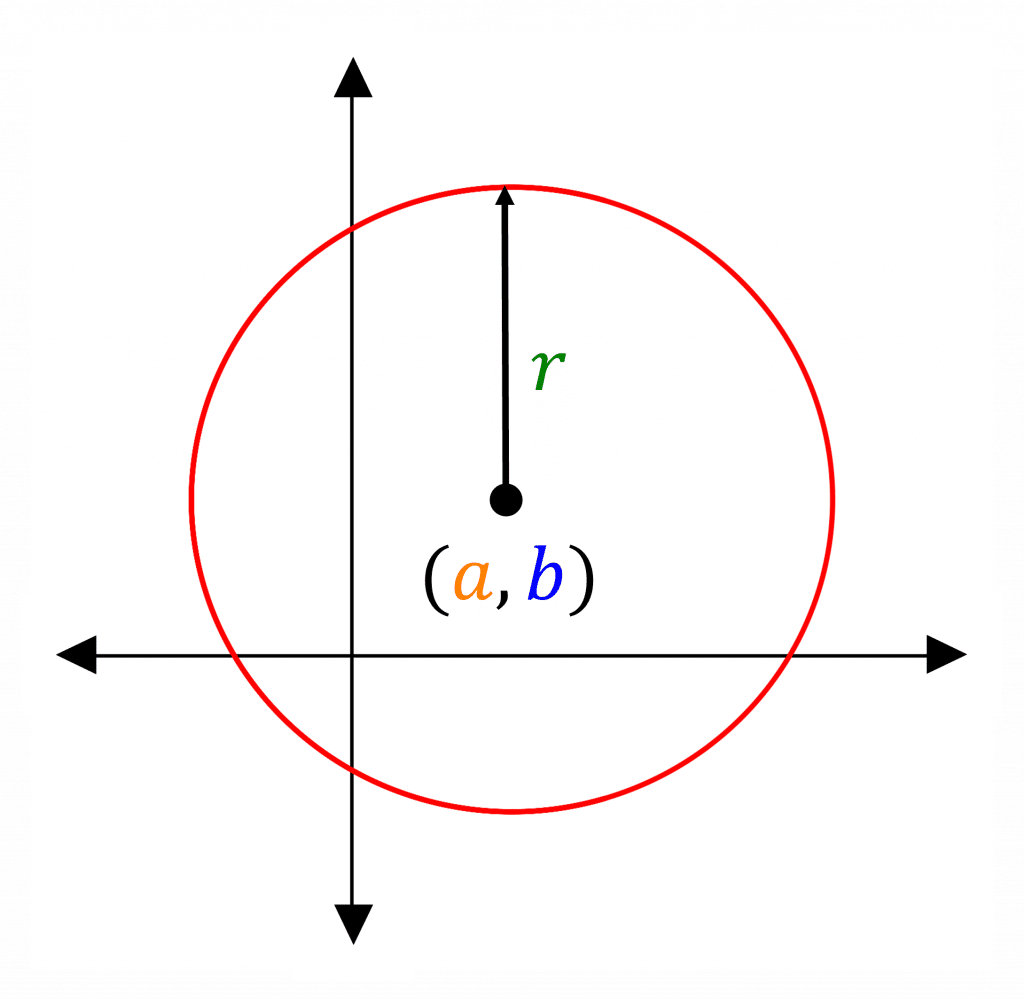
Equation of a Circle
The equation of a circle is
(x-\color{orange}a\color{grey})^{2}+(y-\color{blue}b\color{grey})^{2}=\color{green}r\color{grey}^{2}
This circle has a centre of (\textcolor{orange}{a},\textcolor{blue}{b}) and a radius of \textcolor{green}{r}.
Rearranging a Circle Equation
Some circle equations are not in the form that gives us the centre and radius straight away. However, we can use completing the square to obtain the form we desire.
Example: Find the centre and radius of the circle x^{2}+y^{2}-6x-4y-12=0
(x^{2}-6x)+(y^{2}-4y)-12=0
(x-3)^{2}-9+(y-2)^{2}-4-12=0
(x-3)^{2}+(y-2)^{2}-25=0
(x-3)^{2}+(y-2)^{2}=25
(x-3)^{2}+(y-2)^{2}=5^{2}
Centre is (3,2) and radius is 5.
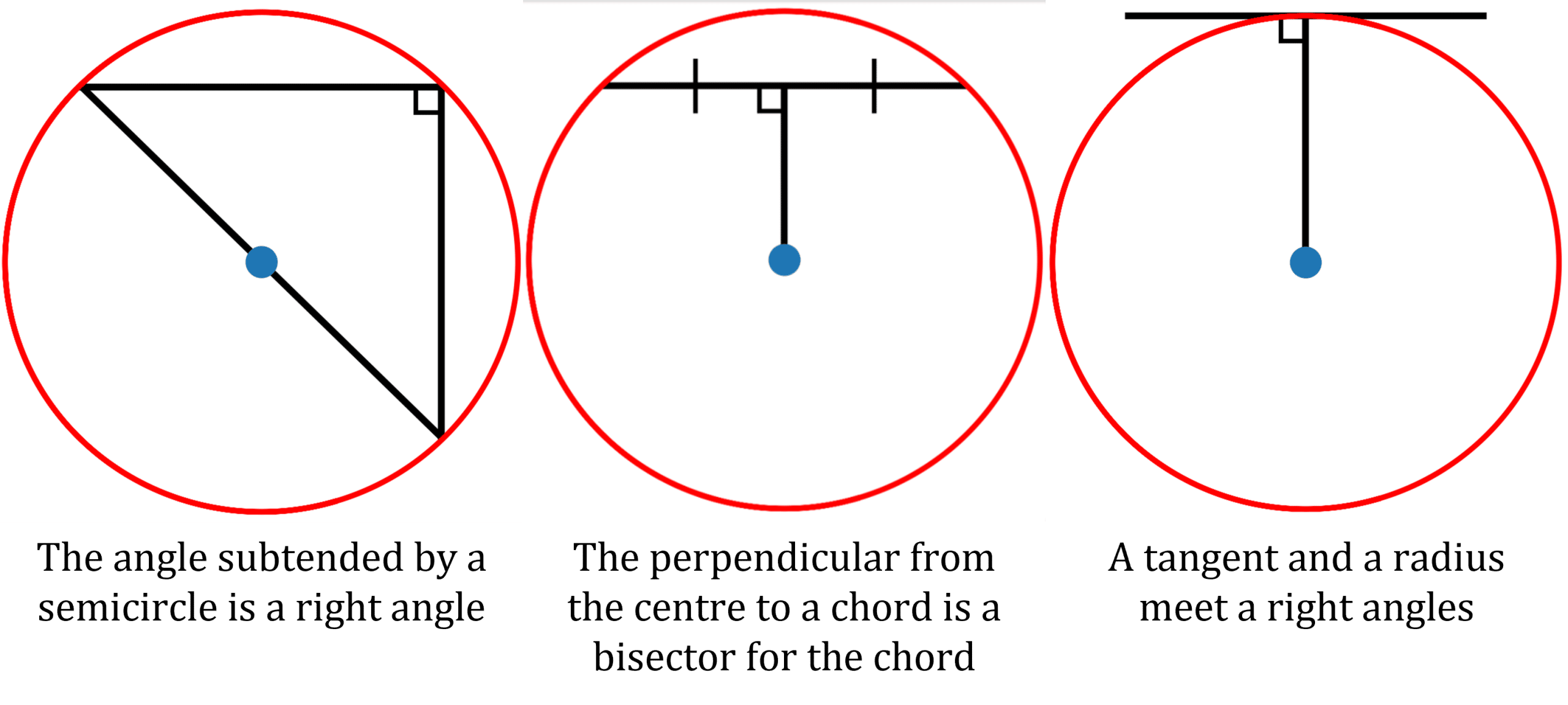
Circle Theorems
There are three circle theorems that are important for circle geometry. They are:
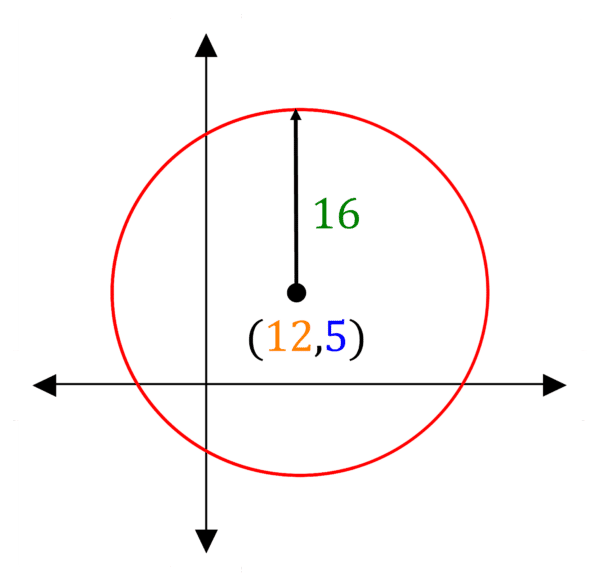
Example 1: Equation of a Circle
Find the equation of this circle, in the form x^{2}+y^{2}+ax+by+c=0.
[2 marks]
Centre is (12,5).
Radius is 16.
Equation is (x-12)^{2}+(y-5)^{2}=16^{2}
x^{2}-24x+144+y^{2}-10y+25=256
x^{2}+y^{2}-24x-10y+169=256
x^{2}+y^{2}-24x-10y-87=0
Example 2: Tangent of a Circle
Find the equation of the tangent of the circle (x-1)^{2}+(y-1)^{2}=25 at the point (4,5), in y=mx+c form.
[5 marks]
Tangent is perpendicular to radius, so we will find the gradient of the radius to obtain the gradient of the tangent.
Centre: (1,1)
So the radius passes through (1,1) and (4,5).
\begin{aligned}\text{gradient of radius}=&\dfrac{5-1}{4-1}\\[1.2em]=&\dfrac{4}{3}\end{aligned}Hence, the tangent has gradient -\dfrac{3}{4}
y-y_{1}=m(x-x_{1})
y-5=-\dfrac{3}{4}(x-4)
y-5=-\dfrac{3}{4}x+3
y=-\dfrac{3}{4}x+8
Circle Geometry Example Questions
Question 1: What are the centre and radius of these circles?
i) (x-1)^{2}+(y-2)^{2}=9
ii) (x+3)^{2}+(y-1)^{2}=25
iii) (x-19)^{2}+(y+21)^{2}=81
[3 marks]
i) Centre: (1,2)
Radius: \sqrt{9}=3
ii) Centre: (-3,1)
Radius: \sqrt{25}=5
iii) Centre: (19,-21)
Radius: \sqrt{81}=9
Question 2: Write the equations of the circles with the following centres and radii:
i) Centre: (3,3)
Radius: 2
ii) Centre: (-1,4)
Radius: 4
iii) Centre: (-10,-17)
Radius: 19
[3 marks]
i) (x-3)^{2}+(y-3)^{2}=4
ii) (x+1)^{2}+(y-4)^{2}=16
iii) (x+10)^{2}+(y+17)^{2}=361
Question 3: Rearrange these equations into the form (x-a)^{2}+(y-b)^{2}=r^{2}:
a) x^{2}+y^{2}+12x+8y+3=0
b) x^{2}+y^{2}-6x-8y+21=0
[4 marks]
a) x^{2}+y^{2}+12x+8y+3=0
(x+6)^{2}-36+(y+4)^{2}-16+3=0
(x+6)^{2}+(y+4)^{2}-49=0
(x+6)^{2}+(y+4)^{2}=49
b) x^{2}+y^{2}-6x-8y+21=0
(x-3)^{2}-9+(y-4)^{2}-16+21=0
(x-3)^{2}+(y-4)^{2}-4=0
(x-3)^{2}+(y-4)^{2}=4
Question 4: Consider the circle (x-4)^{2}+(y-5)^{2}=25.
a) State the centre and radius.
b) Which of these points does the circle pass through?
i) (7,9)
ii) (9,5)
iii) (2,2)
c) Find the equation of the tangent at the point (0, 8).
d) Find the co-ordinates of the point where this tangent touches the x-axis.
[10 marks]
a) Centre: (4,5)
Radius: \sqrt{25}=5
b) To find if a point lies on the circle, substitute it into the equation.
i) (7,9):
(7-4)^{2}+(9-5)^{2}
=3^{2}+4^{2}
=9+16
=25
So (7,9) does lie on the circle.
ii) (9,5):
(9-4)^{2}+(5-5)^{2}
=5^{2}+0^{2}
=25+0
=25
So (9,5) does lie on the circle.
iii) (2,2):
(2-4)^{2}+(2-5)^{2}
=(-2)^{2}+(-3)^{2}
=4+9
=13
So (2,2) does not lie on the circle.
c) Tangent is perpendicular to radius, so gradient of radius will give gradient of tangent.
Radius passes through (4,5) and (0,8)
\begin{aligned}\text{gradient of radius}&=\dfrac{8-5}{0-4}\\[1.2em]&=\dfrac{3}{-4}\\[1.2em]&=-\dfrac{3}{4}\end{aligned}
Hence:
\text{gradient of tangent}=\dfrac{4}{3}
Tangent passes through (0,8)
y-y_{1}=m(x-x_{1})
y-8=\dfrac{4}{3}x
d) Touching x-axis means y=0
0-8=\dfrac{4}{3}x
\dfrac{4}{3}x=-8
x=\dfrac{3}{4}\times(-8)
x=-6
Touches x-axis at (-6,0)
