More Differentiation
More Differentiation Revision
More Differentiation
This section contains further uses of the chain, product and quotient rules, combining them with other things you have learned so far such as trigonometry and stationary points.
Make sure you are happy with the following topics before continuing.
A Level Maths Predicted Papers
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A Level Maths Revision Cards
The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. Maths Made Easy is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
Derivatives of sec, cosec and cot
Use the quotient rule to find the derivatives of \sec(x), \cosec(x) and \cot(x).
Recall: Quotient rule
\dfrac{dy}{dx}=\dfrac{v\dfrac{du}{dx}-u\dfrac{dv}{dx}}{v^{2}}
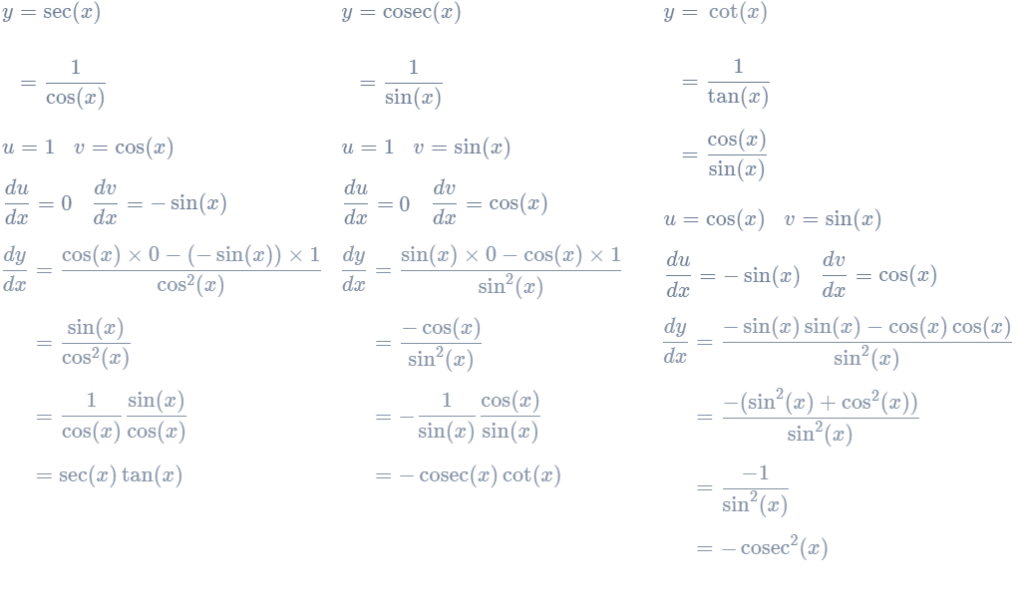
Using the Chain, Product and Quotient Rule With Special Functions
Now that we know how to differentiate every exponential function and every trigonometric function, we can use them along with our rules. Remember when to use each rule:
- Function of a function – chain rule
- Multiplying two functions together – product rule
- Fraction made of functions – quotient rule
Example: Find the derivative of \cosec(4x^{3})
This is a function of a function, so use the chain rule.
\dfrac{dy}{dx}=\dfrac{dy}{dt}\dfrac{dt}{dx}
Take t=4x^{3}.
Then y=\cosec(t)
\dfrac{dy}{dt}=-\cosec(t)\cot(t)
\dfrac{dt}{dx}=12x^{2}
Hence: \dfrac{dy}{dx}=-\cosec(t)\cot(t)12x^{2}
Put x back in:
\dfrac{dy}{dx}=-12x^{2}\cosec(4x^{3})\cot(4x^{3})
Using the Rules Twice
Sometimes you might need to use the chain, product or quotient rule twice to get a derivative.
Example: Differentiate 2x^{2}\cos(e^{x})
This is a product of two functions so use product rule.
\dfrac{dy}{dx}=u\dfrac{dv}{dx}+v\dfrac{du}{dx}
u=2x^{2}\;\;\;v=\cos(e^{x})
\dfrac{du}{dx}=4x
To find \dfrac{dv}{dx} we need to use the chain rule.
\dfrac{dv}{dx}=\dfrac{dv}{dt}\dfrac{dt}{dx}
Take t=e^{x}
Then v=\cos(t)
\dfrac{dv}{dt}=-\sin(t)
\dfrac{dt}{dx}=e^{x}
Hence: \dfrac{dv}{dx}=-\sin(t)e^{x}
Put x back in:
\dfrac{dv}{dx}=-e^{x}\sin(e^{x})Now we can complete our product rule.
\dfrac{dy}{dx}=-2x^{2}e^{x}\sin(e^{x})+4x\cos(e^{x})
Using the Rules to find the Second Derivative
We already know that second derivatives can be very useful when it comes to classifying stationary points. However, starting with expressions like these, finding the second derivative can get very complicated.
Example: y=e^{3x^{2}}. Find \dfrac{d^{2}y}{dx^{2}}.
To differentiate once, we need the chain rule, because this is a function within a function.
\dfrac{dy}{dx}=\dfrac{dy}{dt}\dfrac{dt}{dx}
Take t=3x^{2}
Then y=e^{t}
\dfrac{dy}{dt}=e^{t}
\dfrac{dt}{dx}=6x
Hence: \dfrac{dy}{dx}=6xe^{t}
Put x back in:
\dfrac{dy}{dx}=6xe^{3x^{2}}To differentiate a second time, we notice we have two functions multiplied together, so must use the product rule.
\dfrac{d^{2}y}{dx^{2}}=u\dfrac{dv}{dx}+v\dfrac{du}{dx}
u=6x\;\;\;v=e^{3x^{2}}
\dfrac{du}{dx}=6
\dfrac{dv}{dx} requires the chain rule, but it is identical to the differentiation we just did above.
\dfrac{dv}{dx}=6xe^{3x^{2}}Hence:
\begin{aligned}\dfrac{d^{2}y}{dx^{2}}&=6x\times6xe^{3x^{2}}+6e^{3x^{2}}\\[1.2em]&=36x^{2}e^{3x^{2}}+6e^{3x^{2}}\\[1.2em]&=6(6x^{2}+1)e^{3x^{2}}\end{aligned}
More Differentiation Example Questions
Question 1:
a) State the derivatives of:
i) \sec(x)
ii) \cosec(x)
iii) \cot(x)
b) Find the derivative of \sec(\cot(x)), stating any rules you use.
[5 marks]
a) i) \sec(x)\tan(x)
ii) -\cosec(x)\cot(x)
iii) -\cosec^{2}(x)
b) y=\sec(\cot(x))
This is a function of a function, so use chain rule.
\dfrac{dy}{dx}=\dfrac{dy}{dt}\dfrac{dt}{dx}
Take t=\cot(x)
Then y=\sec(t)
\dfrac{dy}{dt}=\sec(t)\tan(t)
\dfrac{dt}{dx}=-\cosec^{2}(x)
\dfrac{dy}{dx}=-\sec(t)\tan(t)\cosec^{2}(x)
Put x back in
\dfrac{dy}{dx}=-\sec(\cot(x))\tan(\cot(x))\cosec^{2}(x)
Question 2: Differentiate \sin(3x^{2})\ln(x)
[3 marks]
This is a product of two functions, so use product rule.
\dfrac{dy}{dx}=u\dfrac{dv}{dx}+v\dfrac{du}{dx}
u=\sin(3x^{2})\;\;\;v=\ln(x)
\dfrac{dv}{dx}=\dfrac{1}{x}
For \dfrac{du}{dx} we need the chain rule because we have a function within a function.
\dfrac{du}{dx}=\dfrac{du}{dt}\dfrac{dt}{dx}
Take t=3x^{2}
Then y=\sin(t)
\dfrac{du}{dt}=\cos(t)
\dfrac{dt}{dx}=6x
\dfrac{du}{dx}=6x\cos(t)
Put x back in
\dfrac{du}{dx}=6x\cos(3x^{2})
Put into product rule:
\dfrac{dy}{dx}=\dfrac{\sin(3x^{2})}{x}+6x\ln(x)\cos(3x^{2})
Question 3: Find and classify the stationary points of y=9e^{\frac{1}{2}x+\cos(x)} where 0<x<\pi
[8 marks]
First, find the derivative using the chain rule.
\dfrac{dy}{dx}=9\left(\dfrac{1}{2}-\sin(x)\right)e^{\frac{1}{2}x+cos(x)}
Stationary points are where this is equal to 0.
9\left(\dfrac{1}{2}-\sin(x)\right)e^{\frac{1}{2}x+cos(x)}=0
Exponentials can never be equal to 0, so:
9\left(\dfrac{1}{2}-\sin(x)\right)=0
\dfrac{1}{2}-\sin(x)=0
\sin(x)=\dfrac{1}{2}
x=\dfrac{\pi}{6},\dfrac{5\pi}{6}
Find y-coordinate of stationary points:
y=9e^{\frac{1}{2}\times\frac{\pi}{6}+\cos(\frac{\pi}{6})}
y=9e^{\frac{\pi}{12}+\frac{\sqrt{3}}{2}}
y=9e^{\frac{1}{2}\times\frac{5\pi}{6}+\cos(\frac{5\pi}{6})}
y=9e^{\frac{5\pi}{12}-\frac{\sqrt{3}}{2}}
Stationary points are:
\left(\dfrac{\pi}{6},9e^{\frac{\pi}{12}+\frac{\sqrt{3}}{2}}\right),\left(\dfrac{5\pi}{6},9e^{\frac{5\pi}{12}-\frac{\sqrt{3}}{2}}\right)
Next, differentiate again using the product rule.
u=9\left(\dfrac{1}{2}-\sin(x)\right)
v=e^{\frac{1}{2}x+\cos(x)}
\dfrac{du}{dx}=-9\cos(x)
\dfrac{dv}{dx}=\left(\dfrac{1}{2}-\sin(x)\right)e^{\frac{1}2{x}+\cos(x)}
\dfrac{d^{2}y}{dx^{2}}=9\left(\left(\dfrac{1}{2}-\sin(x)\right)^{2}-\cos(x)\right)e^{\frac{1}{2}x-\cos(x)}
Before substituting in x=\dfrac{\pi}{6} and x=\dfrac{5\pi}{6}, we should first notice that the exponential part of the expression is positive for any x, so we need not keep it when trying to determine the sign of \dfrac{d^{2}y}{dx^{2}}.
Want to determine the sign of 9\left(\left(\dfrac{1}{2}-\sin(x)\right)^{2}-\cos(x)\right)
Secondly, we notice that the x values came from \dfrac{1}{2}-\sin(x)=0, so this part will remain 0 when substituting the x values in. We can also get rid of the factor of 9 without changing the sign.
This means that all we need to do is find the sign of -\cos(x).
-\cos\left(\dfrac{\pi}{6}\right)=-\dfrac{\sqrt{3}}{2}<0 so this is a maximum.
-\cos\left(\dfrac{5\pi}{6}\right)=\dfrac{\sqrt{3}}{2}>0 so this is a minimum.
Hence:
\left(\dfrac{\pi}{6},9e^{\frac{\pi}{12}+\frac{\sqrt{3}}{2}}\right) is a maximum.
\left(\dfrac{5\pi}{6},9e^{\frac{5\pi}{12}-\frac{\sqrt{3}}{2}}\right) is a maximum.
You May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.