Composite and Inverse Functions

A LevelAQAEdexcelOCR

Composite and Inverse Functions Revision

Composite and Inverse Functions

A mapping takes an input in one set of values to an output in another set. A function is a type of mapping. You need to be able to understand the language of functions and how to work with composite functions and inverse functions.

Language of Functions

There are some key terms that you need to understand before we look at composite and inverse functions:

A function is an operation that maps each number to only one number, e.g. $x^3$ is $f(x) = x^3$ or $f : x \rightarrow x^3$
The domain is the set of input (starting) values.
The range is the set of possible output values.
The domain and/or range is usually the set of real numbers, denoted $\mathbb{R}$ (i.e. any number, decimal, fraction, surd etc.). If $x$ is any real number then we write $x \in \mathbb{R}$
A function that maps one element in the domain to one element in the range is called a one-to-one function.
A function that maps more than one element in the domain to one element in the range is called a many-to-one function.

Example: State the domain and range of the following functions seen in the graphs:

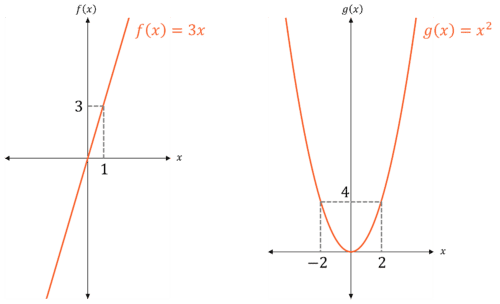
Both functions have domain $x \in \mathbb{R}$ .

$f(x)$ has a range $f(x) \in \mathbb{R}$ and it is a one-to-one function.

$g(x)$ has a range $g(x) \geq 0$ and it is a many-to-one function.

Composite Functions

A composite function is a combination of two or more functions, say $f$ and $g$ , that makes a new function.

We write composite functions as $fg(x)$ which means that we do $g$ first, and then do $f$ – we can rewrite this as $f(g(x))$ to make things clearer. The order is vital – in most cases $fg(x) \neq gf(x)$ (they are different functions).

You may see squared functions, e.g. $f^2 (x)$ – this is the same as $ff(x)$ (you do $f$ twice)

Example: For the functions $\textcolor{red}{f} : x \rightarrow 5x^2 \,\,\, \{ x \in \mathbb{R} \}$ and $\textcolor{limegreen}{g} : x \rightarrow x-1 \,\,\, \{ x\in \mathbb{R} \}$ , find

$\textcolor{red}{f} \textcolor{limegreen}{g}(3)$ , $\textcolor{limegreen}{g} \textcolor{red}{f}(3)$ , $\textcolor{red}{f}^2(x)$ and $\textcolor{red}{f} \textcolor{limegreen}{g}(x)$

$\textcolor{red}{f} \textcolor{limegreen}{g}(3) = \textcolor{red}{f} (\textcolor{limegreen}{g}(3)) = \textcolor{red}{f}(3-1) = \textcolor{red}{f}(2) = 5(2)^2 = 20$

$\textcolor{limegreen}{g} \textcolor{red}{f}(3) = \textcolor{limegreen}{g}( \textcolor{red}{f}(3)) = \textcolor{limegreen}{g}(5(3)^2) = \textcolor{limegreen}{g}(45) = 45 - 1 = 44$

$\textcolor{red}{f} ^2(x) = \textcolor{red}{f} ( \textcolor{red}{f}(x)) = 5(5x^2)^2 = 125x^4$

$\textcolor{red}{f} \textcolor{limegreen}{g} (x) = \textcolor{red}{f} (\textcolor{limegreen}{g}(x)) = \textcolor{red}{f}(x-1) = 5(x-1)^2$

Solving Composite Functions Equations

You may be asked to solve equations involving composite functions, e.g. $fg(x) = 2$ . Just find $fg(x)$ first and then rearrange and solve to find $x$ .

Example: For the functions $\textcolor{red}{f} : x \rightarrow x^2 \,\,\, \{ x \in \mathbb{R} \}$ and $\textcolor{limegreen}{g} : x \rightarrow x+2 \,\,\, \{ x\in \mathbb{R} \}$ , solve

$\textcolor{red}{f} \textcolor{limegreen}{g} (x) = 4$

Also, state the range of $fg(x)$ .

\textcolor{red}{f} \textcolor{limegreen}{g} (x) = \textcolor{red}{f} ( \textcolor{limegreen}{g} (x)) = \textcolor{red}{f} (x+2) = (x+2)^2

So,

$(x+2)^2 = 4$

Rearrange this and solve to find the values of $x$ :

$\begin{aligned} (x+2)^2 &= 4 \\ x+2 &= \pm 2 \end{aligned}$

$x = -4$ or $x = 0$

To find the range, it may be helpful to draw the graph of $\textcolor{red}{f} \textcolor{limegreen}{g} (x)$ :

Hence, the range is $\textcolor{red}{f} \textcolor{limegreen}{g} (x) \geq 0$ .

Inverse Functions

An inverse of a function does the opposite of that function. The inverse of a function $f(x)$ , is written as $f^{-1} (x)$ .

An inverse function maps an element in the range to an element in the domain (the opposite of a function). Hence, only one-to-one functions have inverses.

The domain of the inverse is the same as the range of the function. The range of the inverse is the same as the domain of the function.

A composite function of a function and its inverse, and vice versa, gives $x$ – i.e. $f^{-1}f(x) = ff^{-1} (x) = x$

To work out the inverse of a function, you need to rearrange the function and change the subject.

Example: Find the inverse of $f(x) = 2x^2 + 5$ , with domain $x \textcolor{red}{\geq 0}$ . State the domain and range of $f^{-1} (x)$ .

Step 1: Replace $f(x)$ with $y$ in the equation:

$y = 2x^2 + 5$

Step 2: Rearrange to make $x$ the subject:

$\begin{aligned} y &= 2x^2 + 5 \\[1.1em] y-5 &= 2x^2 \\[1.1em] \dfrac{y-5}{2} &= x^2 \\[1.1em] x &= \sqrt{\dfrac{y-5}{2}} \end{aligned}$

$x \geq 0$ , so we don’t need the negative square root.

Step 3: Replace $x$ with $f^{-1} (x)$ and $y$ with $x$ :

$\textcolor{limegreen}{f^{-1} (x) = \sqrt{\dfrac{x-5}{2}}}$

Step 4: Swap the domain and range:

The domain of $f(x)$ is given as $x \textcolor{red}{\geq 0}$ and its range is $f(x) \textcolor{blue}{\geq 5}$

Hence, the domain of $f^{-1} (x)$ is $x \textcolor{blue}{\geq 5}$ and its range is $f^{-1} (x) \textcolor{red}{\geq 0}$

Note: For simple functions, you can work out the inverse by looking at it – e.g. $f(x) = x-2$ has inverse $f^{-1}(x) = x+2$

Drawing Inverse Functions

For a function $f(x)$ plotted on a graph, its inverse $f^{-1} (x)$ is its reflection in the line $y=x$ .

Example: Given that $f(x) = x^2 - 1$ with domain $x \geq 0$ , sketch the graph of $f^{-1}(x)$ .

Firstly, draw $\textcolor{red}{f(x)}$ . Then draw in the line $y=x$ . Finally, reflect $f(x)$ in $y=x$ to get $\textcolor{blue}{f^{-1}(x)}$ .

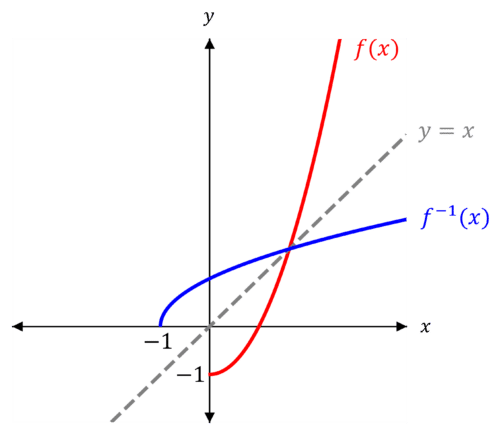
The inverse function is $\textcolor{blue}{f^{-1} (x)} = \sqrt{x+1}$

You can see from the graph that $f(x)$ has domain $x \geq 0$ and range $f(x) \geq -1$ , and $f^{-1} (x)$ has domain $x \geq -1$ and range $f^{-1} (x) \geq 0$ .

Composite and Inverse Functions Example Questions

Question 1: For the functions $f : x \rightarrow x+3, \{ x \in \mathbb{R} \}$ and $g : x \rightarrow \dfrac{2}{2x+1}, \{ x \neq - \dfrac{1}{2} \}$ , find

a) $gf(x)$

b) $fg(3)$

[4 marks]

$\begin{aligned} gf(x) &= g(f(x)) \\[1.1em] &= g(x+3) \\[1.1em] &= \dfrac{2}{2(x+3)+1} \\[1.1em] &= \dfrac{2}{2x+7} \end{aligned}$

$\begin{aligned} fg(3) &= f(g(3)) \\[1.1em] &= f \left( \dfrac{2}{2(3)+1} \right) \\[1.1em] &= f \left ( \dfrac{2}{7} \right) \\[1.1em] &= \dfrac{2}{7} + 3 \\[1.1em] &= \dfrac{23}{7} \end{aligned}$

Save your answers with

Gold Standard Education

Question 2: For the function $f : x \rightarrow 2x^2 - 3, \{ x \in \mathbb{R} \}$ , find

a) $f^2(x)$

b) $f^2(2)$

[3 marks]

$\begin{aligned} f^2(x) &= f(f(x)) \\ &= 2(2x^2 - 3)^2 - 3 \\ &= 2(4x^4 - 12x^2 + 9) - 3 \\ &= 8x^4 - 24x^2 + 18 - 3 \\ &= 8x^4 - 24x^2 + 15 \end{aligned}$

$f^2(2) = 8(2)^4 - 24(2)^2 + 15 = 47$

Save your answers with

Gold Standard Education

Question 3: For the functions $f : x \rightarrow x^2 +3, \{ x \in \mathbb{R} \}$ and $g : x \rightarrow \dfrac{6}{x-2}, \{ x \neq 2 \}$ , solve $gf(x) = 2$

[3 marks]

$\begin{aligned} gf(x) &= g(f(x)) \\[1.1em] &= \dfrac{6}{(x^2 + 3) - 2} \\[1.1em] &= \dfrac{6}{x^2 + 1} \end{aligned}$

So, we can solve the equation to find $x$

$\begin{aligned} gf(x) &= 2 \\ \dfrac{6}{x^2 + 1} &= 2 \\ 6 &= 2(x^2 + 1) \\ 6 &= 2x^2 + 2 \\ 4 &= 2x ^2 \\ 2 &= x^2 \\ x &= \pm \sqrt{2} \end{aligned}$

Save your answers with

Gold Standard Education