Variable Oxidation State
Variable Oxidation State Revision
Variable Oxidation States
Transition elements can exist in variable oxidation states. These variable oxidation states allow for transition metals to be used as oxidising agents and reducing agents within a range of different reactions.
The Oxidation States of Transition Metals
A lot of transition elements are able to exist in variable oxidation states meaning that their oxidation number can vary. For example, manganese can exist with oxidation states of +2, +3, +4, +6 or +7. It is important to note that ions with lower oxidation states can exist as simple ions, so we can have \text{Mn}^{2+} or \text{Mn}^{3+}. However, when we begin reaching higher oxidation states, such as +7, the atoms cannot exist as simple ions and must be part of a complex such as \text{MnO}_4^{-}.
The oxidation states of transition metals can affect the properties they possess.
- Transition metals with low oxidation states, such as \text{V}^{2+}, usually act as reducing agents.
- Transition metals with high oxidation states, such as \text{MnO}_4^-, tend to act as oxidising agents.
Vanadium
Vanadium is a good example of a transition metal that has variable oxidation states from +2 to +5. These different oxidation states can be achieved by reducing Vanadate (V) ions, in ammonium metavanadate, with zinc in acidic conditions. Zinc in an acidic solution acts as a very strong reducing agent, so it can reduce a lot of transition metal ions to lower oxidation states.
When ammonium metavanadate reacts with zinc in acidic conditions a series of reactions take place. First, Vanadium (V) is reduced to Vanadium (IV), turning the solution from yellow to blue.
2\text{VO}_2^{+} + \text{Zn} + 4\text{H}^{+} \rarr 2\text{VO}^{2+} + \text{Zn}^{2+} + \text{H}_2\text{O}
Second, Vanadium(IV) is reduced to Vanadium (III), turning the solution from blue to green.
2\text{VO}^{2+} + \text{Zn} + 4\text{H}^+ \rarr 2\text{V}^{3+} + \text{Zn}^{2+} + 2\text{H}_2\text{O}
Thirdly, Vanadium(III) is reduced to Vanadium (II), turning the solution from green to violet.
2\text{V}^{3+} + \text{Zn} \rarr 2\text{V}^{2+} + \text{Zn}^{2+}
| Vanadium Ion | Oxidation State | Colour |
| \text{VO}_2^+ | +5 | Yellow |
| \text{VO}^{2+} | +4 | Blue |
| \text{V}^{3+} | +3 | Green |
| \text{V}^{2+} | +2 | Violet |
Redox Potentials
The redox potential is a measure of how readily an ion or atom is reduced or oxidised. A more positive redox potential shows that an ion or atom is more likely to be reduced.
Redox potentials are very similar to an electrode potential except for the fact that redox potentials are dependent upon \text{pH} and ligands.
\underline\text{pH}
The redox potential can be affected by \text{pH}. In more acidic conditions, the redox potentials are larger, and the ions are more readily reduced. An example of this is with manganese in a manganate (VII) ion. The half equation for the reduction of manganese is as follows.
\text{MnO}_4^- + 8\text{H}^+ + 5\text{e}^- \rarr \text{Mn}^{2+} + 4\text{H}_2\text{O} \text{ E}^{\varnothing} = +1.51\text{ V}
In this half equation an acid provides the \text{H}^+ ions that allow for the reaction to take place. When the acid is limited another reaction takes place which has a lower E-cell value.
\text{MnO}_4^- + 2\text{H}_2\text{O} + 3\text{e}^- \rightleftharpoons \text{MnO}_2 + 4\text{OH}^- \text{ E}^{\varnothing} = +0.59\text{ V}
Ligands
The redox potential can also be affected by changing the ligand. Ligands can alter the redox potentials dependent on how they bind to the ion in a specific oxidation state. A good example of this is when ammonia ligands are compared to water ligands.
The following two half equations show the difference in E-cell value when ammonia is a ligand compared to when water is a ligand.
\left[\text{Co}\left(\text{H}_2\text{O}\right)_6\right]^{2+} + 2\text{e}^- \rightleftharpoons \text{Co} + 6\text{H}_2\text{O} \text{ E}^{\varnothing} = -0.28\text{ V}
\left[\text{Co}\left(\text{NH}_3\right)_6\right]^{2+} + 2\text{e}^- \rightleftharpoons \text{Co} + 6\text{NH}_3 \text{ E}^{\varnothing} = -0.43\text{ V}
The difference in values is caused by the fact that ammonia is a stronger ligand than water so binds more strongly to cobalt. This causes a lower E-cell value which shows that the equilibrium lies a bit more to the left and that the complex is less readily reduced or oxidised.
Tollens Reagent
Tollens’ reagent contains the complex silver nitrate, \left[\text{Ag}\left(\text{NH}_3\right)_2\right]^+, and is used to distinguish between aldehydes and ketones.
When Tollens’ reagent is added to aldehydes, the aldehyde reduces the silver ion within the complex to silver. This produces a mirrored layer of solid silver around the walls of the reaction vessel.
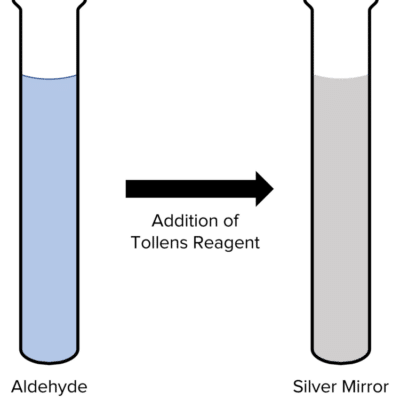
Reduction Half-Equation: \left[\text{Ag}\left(\text{NH}_3\right)_2\right]^+ + \text{e}^- \rarr \text{Ag} + 2\text{NH}_3
Oxidation Half-Equation: \text{RCHO} + \text{H}_2\text{O} \rarr \text{RCOOH} + 2\text{H}^+ + 2\text{e}^-
General Overall Equation: \text{RCHO} + 2\left[\text{Ag}\left(\text{NH}_3\right)_2\right]^+ + 3\text{OH}^- \rarr \text{RCOO}^- + 2\text{Ag} + 4\text{NH}_3 + 2\text{H}_2\text{O}
Note: In the above equations, R indicates a hydrocarbon chain.
Redox Titrations
A redox titration is a type of titration where the concentration of a substance is measured based on a redox reaction. In other words, it is used to determine the amount of oxidising agent used to react with a certain amount of reducing agent.
Calculating concentration from a redox titration is very similar to calculating it from an acid-base titration. It involves the same steps and calculations but the only difference is that the equation used to find ratios would be an overall redox equation.
In most questions, the overall redox equation is constructed from half equations. There are three main half equations you should learn for redox titrations.
\text{Fe}^{2+} \rarr \text{Fe}^{3+} + \text{e}^-
\text{C}_2\text{O}_4^{2-} \rarr 2\text{CO}_2 + 2\text{e}-
\text{MnO}_4^- + 8\text{H}^+ + 5\text{e}^- \rarr \text{Mn}^{2+} + \text{H}_2\text{O}
The majority of questions can be answered using these half equations, but make sure you know how to find half equations and overall equations in case the half-equation required is not one of the above.
Example: Manganate Redox Titration
In an acidic solution, 5\text{ cm}^{-3} of a sodium ethanedioate solution is oxidised by 24\text{ cm}^{-3} of 0.06\text{ mol dm}^{-3} of potassium manganate (VII). Calculate the concentration, in \text{ mol dm}^{-3}, of the sodium ethanedioate solution.
First, combine the two half equations for manganate ions and ethanedioate to form an overall equation.
2\text{MnO}_4^- + 16\text{H}^+ + 5\text{C}_2\text{O}_4^{2-} \rarr 2\text{Mn}^{2+} +8\text{H}_2\text{O} + 10\text{CO}_2
Using information given in the question, calculate the moles of \text{MnO}_4^-.
\text{Moles of MnO}_4^- = \frac{24}{1000} \times 0.06 = 1.44\times10^{-3}\text{ mol}
Work out the ratio of \text{MnO}_4^- to \text{C}_2\text{O}_4^{2-} using the overall redox equation. Then use that to calculate the moles of \text{C}_2\text{O}_4^{2-}.
\text{Ratio MnO}_4^- \text{ to } \text{C}_2\text{O}_4^2- = 2:5
\text{Moles of C}_2\text{O}_4^{2-} = 1.44\times10^{-3} \times \frac{5}{2} = 3.6\times10^{-3}\text{ mol}
Finally, calculate the concentration of sodium ethanedioate using the information worked out (moles) and that given in the question (volume).
\text{Concentration of Sodium Ethanedioate} = 3.6\times10^{-3}\times \frac{5}{1000} = 0.72\text{ mol dm}^{-3}
Variable Oxidation State Example Questions
Question 1: The element vanadium can exist in a range of oxidation states. One ion of vanadium is the \text{VO}^{2+} ion.
a.) Give the oxidation states of vanadium in \text{VO}^{2+}.
b.) Give the colour of the \text{VO}^{2+} ion.
[2 marks]
a.) +4
b.) Blue
Question 2: Give the reduction half-equation for the reaction of Tollens reagent with an aldehyde.
[2 marks]
\left[\text{Ag}\left(\text{NH}_3\right)_2\right]^+ + \text{e}^- \rarr \text{Ag} + 2\text{NH}_3
Question 3: Give two factors that can affect the redox potential of a transition metal.
[2 marks]
- \text{pH}
- The ligands bonded to the central metal ion.
Question 4: 25.0\text{ cm}^{-3} of a solution of \text{H}_2\text{O}_2 is acidified and then reacted with 15.8\text{ cm}^{-3} of a 0.0200\text{ mol dm}^{-3} solution of potassium manganate (VII). The equation for the reaction is below.
2\text{MnO}_4^- + 6\text{H}^+ + 5\text{H}_2\text{O}_2 \rarr 2\text{Mn}^{2+} + 8\text{H}_2\text{O} + 5\text{O}_2Using this equation, determine the concentration, in \text{ g dm}^{-3}, of the \text{H}_2\text{O}_2 solution.
[4 marks]
\begin{aligned}\text{Moles KMnO}_4&=\frac{15.8 }{1000}\times 0.020\\\text{}\\&=3.16\times10^{-4}\text{ mol}\end{aligned}
\begin{aligned}\text{Moles H}_2\text{O}_2 &= 3.16\times10^{-4} \times \frac{5}{2} \\&= 7.9\times10^{-4}\text{ mol}\end{aligned}
\begin{aligned}\text{Moles H}_2\text{O}_2\text{ in } 1000\text{ cm}^{-3}&=4\times7.9\times10^{-4}\\\text{}\\&=0.0316\text{ mol}\end{aligned}
\begin{aligned}\text{Concentration of H}_2\text{O}_2&=0.0316\times34\\&=1.07\text{ g dm}^{-3}\end{aligned}
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.