Calculating the EMF
Calculating the EMF Revision
Calculating the EMF
The EMF (electromotive force) of a cell is the maximum potential difference between two electrodes of a cell. EMF is measure by combining two separate half cells. The \text{E}^{\varnothing} of individual half cells can also be used to predict overall chemical reactions.
Cell Potentials
Half-cell potentials are measured compared to the standard hydrogen electrode. The standard potentials of half cells can be both positive and negative. The value of a standard potential will show whether a half cell undergoes reduction or oxidation in a given cell.
The more negative the cell potential of a substance, the easier it will be for the substance to oxidise other substances and to act as an oxidising agent. The more positive the cell potential of a substance, the easier it will be for the substance to reduce other substances and to act as a reducing agent.
Cell potentials are calculated by subtracting the potential of the half-cell on the right of the cell in the conventional cell representation from the potential of the half-cell on the left.
\text{EMF}=\text{E}^{\varnothing}_\text{Right}-\text{E}^{\varnothing}_\text{Left}
Cell potentials are often listed in a table known as the electrochemical series. This table displays the half equations of half cell reactions and the voltages these produce in descending order from most to least positive. The SHE is found in the middle of this list. An excerpt is presented below.
| Half Cell Reaction | \text{E}^{\varnothing}\text{ /V} |
| \text{Cu}^{2+}_{\text{(aq)}}+2\text{e}^-\rarr\text{Cu}_{\text{(s)}} | 0.34 |
| \text{Sn}^{4+}_{\text{(aq)}}+2\text{e}^-\rarr\text{Sn}^{2+}_{\text{(aq)}} | 0.15 |
| 2\text{H}^+_{\text{(aq)}}+\text{e}^-\rarr\text{H}_2\text{ (SHE)} | 0 |
| \text{Pb}^{2+}_{\text{(aq)}}+2\text{e}-\rarr\text{Pb}_{\text{(s)}} | -0.13 |
| \text{Ni}^{2+}_{\text{(aq)}}+2\text{e}^+\rarr\text{Ni}_{\text{(s)}} | -0.26 |
Redox Reactions
The electrochemical series can be used to predict the overall redox reactions that may take place when two substances are mixed. We are able to do this by comparing the values of the \text{E}^{\varnothing} of the substances half cells.
The half equations in the electrochemical series as always written in the direction of reduction. For example, the reaction of the nickel half cell is written as:
\text{Ni}^{2+}_{\text{(aq)}}+2\text{e}^-\rarr\text{Ni}_{\text{(s)}}
The direction of the the half cell reaction in an overall reaction will depend however on whether or not it has a more or less negative value of \text{E}^{\varnothing} than that of the substance it is reacting with.
The more positive half cell will oxidise substances so the reaction will happen in the direction of reduction (i.e. from left to right), just as written in the electrochemical series. The more negative half cell will reduce substances so the reaction will happen in the direction of oxidation (i.e. from right to left).
For example, if nickel were the most negative half-cell in a reaction, the equation would procced from right to left:
\text{Ni}_{\text{(s)}}\rarr\text{Ni}^{2+}+2\text{e}^-
By using the half equations listed in the electrochemical series, it is possible to build an overall reaction between two substances. We can calculate the EMF of these reactions by subtracting the \text{E}^{\varnothing} of the oxidising half cell from that of the reducing half cell.
\text{EMF}=\text{E}^{\varnothing}_{\text{Reduction}}-\text{E}^{\varnothing}_{\text{Oxidation}}
Required Practical
Measuring the EMF of an Electrochemical Cell
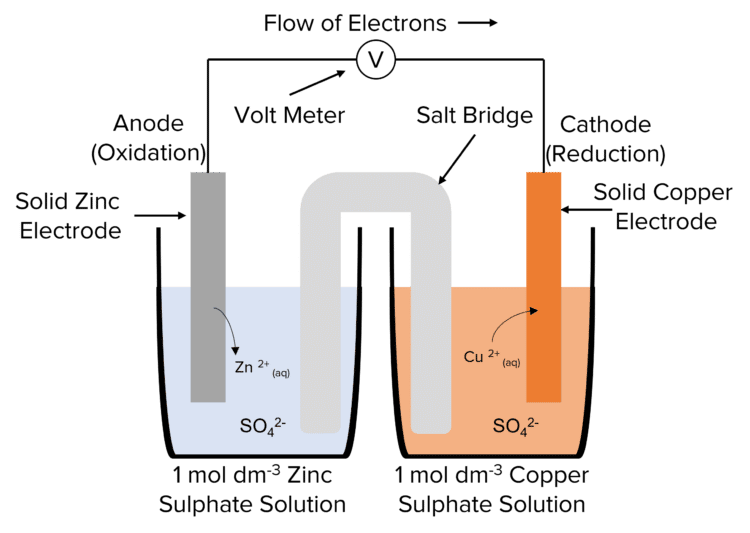
Method
- Choose a strip of two metals to carry out the experiment. These metals can be any from copper, iron, silver or zinc.
- Clean the metals using emery paper, so that the oxide layer is removed, and ensure that there is no grease on the metals which can affect the results.
- Place one metal strip into a 100\text{ cm}^3 beaker and fill the beaker with 50\text{ cm}^3 of a solution containing the metal ions. Repeat this for the second metal, using a different beaker.
- Dip a strip of filter paper into an inert salt solution, such as \text{KNO}_3, and then place each end of the strip into the separate beakers. Ensure that the strip is in the solutions.
- Using crocodile clips, connect the metals to a voltmeter and create a circuit.
- Measure and record the voltage of the cell.
Effect of Conditions on Cell Voltage
Le Châtelier’s principle can be used to understand the effect of changing conditions on the electrode potential of a cell.
If the EMF of a cell is more positive, then the reaction is more likely to occur spontaneously. Despite this, it is possible that reactions with a positive EMF will not occur since some reactions happen so slowly as to be effectively inert or have a high activation energy.
Increasing the concentration of reactants in a cell increases EMF. This is because the equilibrium shifts toward the products of the reaction, producing fewer electrons. Most cell reactions are exothermic. As such, increasing the temperature would cause a decrease in the EMF by shifting the equilibrium towards reactants, in the endothermic direction. Increasing the pressure in a cell would cause the EMF to decrease because more electrons would be produced.
Example 1: Calculating Cell E.M.F
Calculate the EMF for the following electrochemical cell.
\text{Mg}_{\text{(s)}}\vert\text{Mg}{2+}_{\text{(aq)}}\Vert\text{Cu}^{2+}_{\text{(aq)}}\vert\text{Cu}_{\text{(s)}}
Standard Electrode Values
\text{Mg}^{2+}_{\text{(aq)}}\vert\text{Mg}_{\text{(s)}}\text{ E}^{\varnothing} = \textcolor{#00bfa8}{-2.38\text{ V}}
\text{Cu}^{2+}_{\text{(aq)}}\vert\text{Cu}_{\text{(s)}}\text{ E}^{\varnothing} = \textcolor{#f21cc2}{+0.34\text{ V}}
[2 marks]
\begin{aligned}\text{EMF} &= \text{E}^{\varnothing}_{\text{Reduction}} - \text{E}^{\varnothing}_{\text{Oxidation}}\\ &= \textcolor{#f21cc2}{0.34} - \textcolor{#f21cc2}{(-2.38)}\\ &= \textcolor{#00bfa8}{+2.72\text{ V}}\end{aligned}
Example 2: Deducing the Overall Reaction of a Cell
Write the overall equation for the electrode reactions below.
\text{Au}^+_{\text{(aq)}} + \text{e}^-\rarr\text{Au}_{\text{(s)}}\text{ E}^{\varnothing} = \textcolor{#00bfa8}{+1.68\text{ V}}
\text{Ni}^{2+}_{\text{(aq)}}+2\text{e}^-\rarr\text{Ni}_{\text{(s)}}\text{ E}^{\varnothing} = \textcolor{#f21cc2}{-0.25\text{ V}}
[4 marks]
As the more negative electrode will contain the oxidising anent of the reaction, this electrode reduces other substances of the reaction, and the reaction will go backwards. So we can rewrite the reaction at the nickel electrode.
\text{Ni}_{\text{(s)}}\rarr\text{Ni}^{2+}_{\text{(aq)}}+2\text{e}^-
The gold electrode oxidises other substances so the reaction goes from left to right and it doesn’t need to be rearranged.
However, in the first reaction, there is only one electron, and in the second there are two. To combine these equations, we need to double the gold equation, so the electrons are equal.
2\text{Au}^+_{\text{(aq)}} + 2\text{e}^-\rarr2\text{Au}_{\text{(s)}}
Next, we combine the two new equations.
\text{Ni}_{\text{(s)}} + 2\text{Au}^+_{\text{(aq)}} +2\text{e}^-\rarr\text{Ni}^{2+}_{\text{(aq)}} + 2\text{e}^- + 2\text{Au}_{\text{(s)}}
Lastly, to get the overall equation, we can remove the electrons.
\text{Ni}_{\text{(s)}} + 2\text{Au}^+_{\text{(aq)}}\rarr\text{Ni}^{2+}_{\text{(aq)}} + 2\text{Au}_{\text{(s)}}
Calculating the EMF Example Questions
Question 1: Nickel-Cadmium cells are used in portable electrical products.
The electrode reactions that take place in the cell are shown below.
\text{NiO(OH)} + \text{H}_2\text{O} + \text{e}^-\rarr \text{Ni(OH)}_2 +\text{OH}^- \text{ E}^{\varnothing} = +0.52\text{ V}
\text{Cd(OH)}_2 + 2\text{e}^-\rarr \text{Cd} + 2\text{OH}^-\text{ E}^{\varnothing} = -0.88\text{ V}
Deduce the overall reaction for the cell. Calculate its EMF.
[3 marks]
The \text{NiO(OH)} half cell equation contains 1 electron and the \text{Cd(OH)}_2 electrode half equation contains 2 electrons. Therefore the \text{NiO(OH)} half equation is multiplied by two to give:
2\text{NiO(OH)} + 2\text{H}_2\text{O} + \text{Cd} → 2\text{Ni(OH)}_2 + \text{Cd(OH)}_2
1.4\text{ V}
(Two marks for correct equation. One mark for correct potential.)
Question 2: Identify the oxidising agent in the overall reaction in the cell detailed above.
[1 mark]
NiO(OH) or Ni(II)
Question 3: Below is a conventional representation of a lithium cell.
\text{Li}_{\text{(s)}}\vert\text{Li}^+_{\text{(aq)}}\Vert\text{Li}^+_{\text{(aq)}}\vert\text{MnO}_{2\text{(s)}}, \text{LiMnO}_{2\text{(s)}}\vert\text{Pt}_{\text{(s)}}\text{ E}^{\varnothing} = +2.91\text{ V}
Write the half-equation for the reaction that occurs at the positive electrode of this cell.
[1 mark]
\text{Li}^+ + \text{MnO}_2 + \text{e}^-\rarr \text{LiMnO}_2
Question 4: An experiment is carried out to measure the e.m.f. of the following cell.
\text{Al}_{\text{(s)}}\vert\text{Al}^{3+}_{\text{(aq)}}\Vert\text{H}^+_{\text{(aq)}}\vert\text{H}_{2\text{(g)}}\vert\text{Pt}_{\text{(s)}}
The aluminium that is used as an electrode is rubbed with emery paper. Why?
[1 mark]
To remove the oxide layer.
Question 5: In a cell, the following reactions take place at each electrode.
\text{Zn}^{2+}_{\text{(aq)}} + 2\text{e}^-\rarr\text{Zn}_{\text{(s)}}\text{ E}^{\varnothing} = -0.76\text{ V}
\text{Fe}^{2+}_{\text{(aq)}} + 2\text{e}^- \rarr\text{Fe}_{\text{(s)}}\text{ E}^{\varnothing} = -0.44\text{ V}
State the effect, on the EMF of decreasing the concentration of \text{Zn}^{2+}.
[2 mark]
The equilibrium of the reaction would shift to the product side, reducing the number of electrons produced. Therefore EMF would increase.
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.