Revise
Recurring Decimals to Fractions
Recurring Decimals to Fractions Revision
Recurring Decimals to Fractions
In this topic, we’ll look at how to go from a recurring decimal to a fraction and vice versa.
What are Recurring Decimals?
A recurring decimal is any number with a repeated digit or section of repeated digits after a decimal point. We show this with a dot above both the start and the end of the repeated section.
\begin{aligned} \dfrac{1}{3} &= 0.\dot{3} = 0.33333... \\ \dfrac{6}{11} &= 0.\dot{5}\dot{4} = 0.54545454... \end{aligned}
Note: Fractions in which the denominator has prime factors of only 2 or 5 will terminate (not repeat).
Method 1: Convert Fractions to Recurring Decimals
To convert a fraction to a recurring decimal, we can find an equivalent fraction that only contains 9‘s on the denominator. The numerator then gives us the recurring (repeating) part of the decimal, in which we put a dot above the first number and the last number.
Example: Write \dfrac{2}{11} as a recurring decimal.
Multiply the top and the bottom of the fraction by 9 to make the denominator have 9‘s in it:
\dfrac{2}{11} = \dfrac{18}{99}
Then the numerator, 18 gives us the recurring part, so we put a dot above the 1 and a dot above the 8. So,
\dfrac{2}{11} = 0.\dot1 \dot8
Method 2: Convert Fractions to Recurring Decimals
Another way to convert a fraction to a recurring decimal is to treat the fraction like a division and use some method of division to divide the numerator by the denominator. Here we will use the bus stop method.
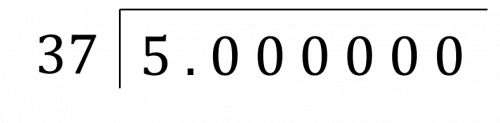
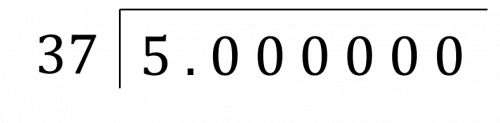
Example: Write \dfrac{5}{37} as a decimal.
We set up the bus stop method as follows, with several zeros after the decimal place.
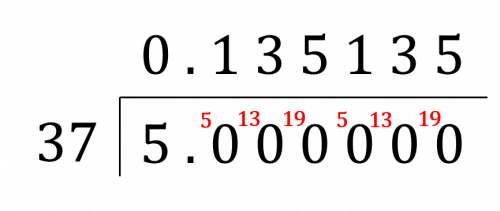
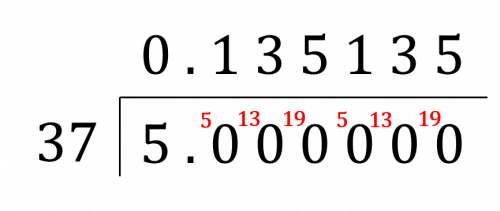
Then complete the bus stop method, as follows.
As the decimal repeats itself, it is a recurring decimal which can be written as 0.\dot1 3 \dot5. So,
\dfrac{5}{37} = 0.\dot1 3 \dot5
Convert Recurring Decimals to Fractions
Converting a recurring decimal to a fraction can be a stand alone exam question so it is certainly a skill you want to master.
Example: Write 0.\dot1 4 \dot7 as a fraction in its simplest from.
Step 1: Make your number equal to x.
x= 0.\dot1 4 \dot7
Step 2: Multiply both sides by \textcolor{blue}{10} for each decimal place that isn’t recurring (If there are none, it stays as Step 1).
x= 0.\dot1 4 \dot7
Step 3: Multiply both sides by \textcolor{blue}{10} for each number that is recurring.
1000x = 147.\dot1 4 \dot7
Step 4: Subtract the equations in steps 2 and 3 so that the numbers after the decimal point cancel, then solve for x.
\begin{aligned} 1000x - x &= 147.\dot1 4 \dot7 - 0.\dot1 4 \dot7 \\ 999x &= 147 \\ x &= \dfrac{147}{999} \end{aligned}
Step 5: Simplify the fraction if required.
x = \dfrac{49}{333}
Example 1: Fraction to Decimal
Write \dfrac{7}{33} as a decimal.
[2 marks]
The first thing we need to do is set up the bus stop method.
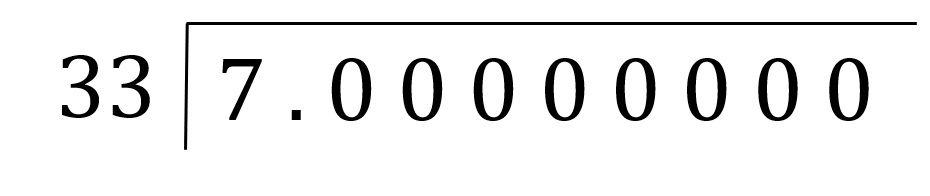
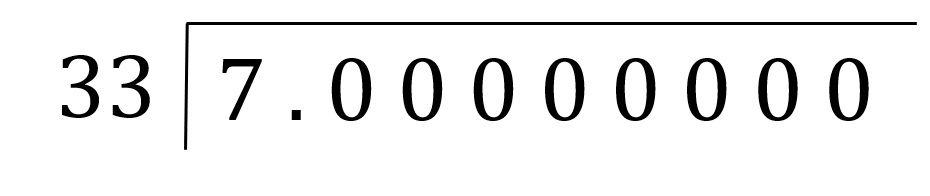
So, the set up should look like.
Then look to complete the bus stop method.
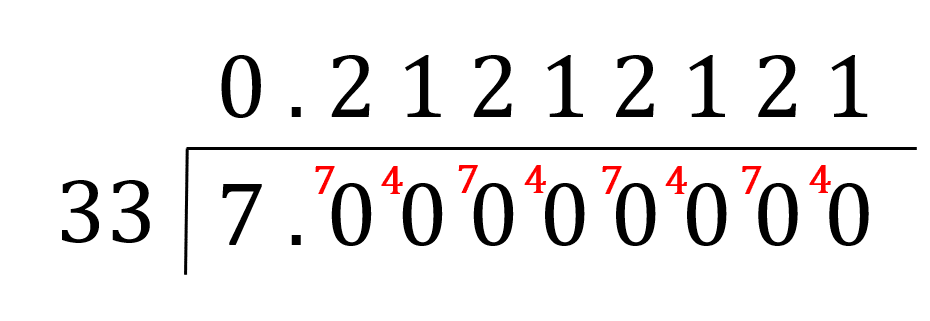
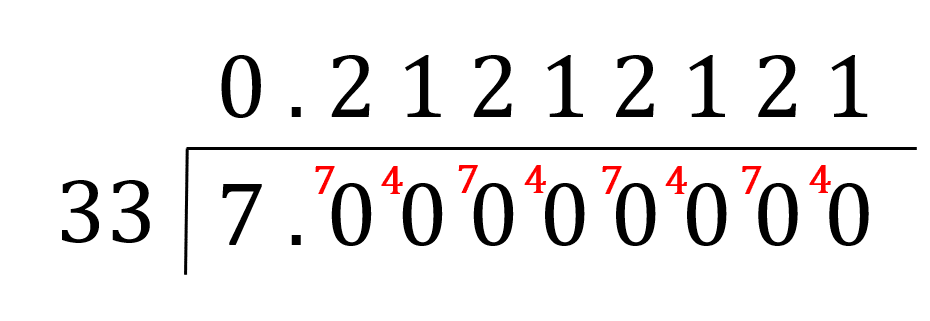
As the decimal repeats itself, it is a recurring decimal which can be written as 0.\dot{2}\dot{1}. So,
\dfrac{7}{33} = 0.\dot2 \dot1
Example 2: Recurring Decimal to Fraction
Write 0.\dot{1}\dot{4} as a fraction.
[2 marks]
So, set x = 0.\dot{1}\dot{4}, the thing we want to convert to a fraction. Then,
100x = 14.\dot{1}\dot{4}.
Now that we have two numbers, x and 100x, with the same digits after the decimal point, if we subtract one from another, the numbers after the decimal point will cancel.
\begin{aligned} 100x -x &= 14.\dot{1}\dot{4} - 0.\dot{1}\dot{4} \\ 99x &= 14 \end{aligned}
Then, if we divide both sides of this by 99, we get
x = \dfrac{14}{99}
Example 3: Recurring Decimal to Fraction
Write 0.8\dot{3} as a fraction.
[2 marks]
So, let x = 0.8\dot{3}. This time, we take 10x = 8.\dot{3} and 100x = 83.\dot{3}, then we have two multiples of x that have the same digits after the decimal point.
So, subtracting one from the other, we get
\begin{aligned} 100x - 10x &= 90x \\ 83.\dot{3} - 8.\dot{3} &= 83 - 8 = 75 \\ 90x &= 75 \end{aligned}
Dividing both sides by 90, we get that
x = \dfrac{75}{90} = \dfrac{5}{6}
Recurring Decimals to Fractions Example Questions
Question 1: Write \dfrac{1}{9} as a recurring decimal.
[2 marks]
Treating this fraction as a division, we will use the bus stop method to find the result of dividing 1 by 9. The result of the division should look like,
\;\;\;\;0.\;1\;1\;1\;1\;1\;\\9\overline{\left)1.0{}^10{}^10{}^10{}^10\right.}
Hence,
\dfrac{1}{9} = 0.\dot{1}
Question 2: Write 0.\dot{3} as a fraction.
[2 marks]
If we let x=0.\dot{3} and 10x=3.\dot{3}
Then x and 10x are identical after the decimal place. Hence if we subtract one from the other then everything after the decimal point shall cancel.
10x - x = 9x = 3.\dot{3} - 0.\dot{3} = 3
Thus if we rearrange to make x the subject then,
x=\dfrac{3}{9}=\dfrac{1}{3}
Question 3: Write 0.\dot{3}9\dot{0} as a fraction.
[2 marks]
If we let x = 0.\dot{3}9\dot{0} and 1,000x = 390.\dot{3}9\dot{0}
Then x and 1,000x are identical after the decimal place. Hence if we subtract one from the other then everything after the decimal point shall cancel.
1,000x - x = 999x = 390.\dot{3}9\dot{0} - 0.\dot{3}9\dot{0} = 390
Thus if we rearrange to make x the subject then,
x = \dfrac{390}{999}
This simplifies to,
x = 0.\dot{3}9\dot{0} = \dfrac{130}{333}
Question 4: Write \dfrac{10}{11} as a recurring decimal.
[2 marks]
Treating this fraction as a division, we will use short division to find the result of dividing 10 by 11. The result of the short division should look like,
\;\;\;\;\;0\;\;.9\;\;0\;\;9\;\;0\;\;9\;\;0\;\;9\;\;0\\11\overline{\left)10.0{}^10{}^{10}0{}^10{}^{10}0{}^10{}^{10}0{}^10\right.}
Hence,
\dfrac{10}{11} = 0.\dot{9}\dot{0}
Question 5: Write 1.5\dot{4} as a fraction.
[2 marks]
If we let x = 1.5\dot{4} then 10x = 15.\dot{4} and 100x = 154.\dot{4}
Then, both 10x and 100x are identical after the decimal place. Hence, we are able to subtract one from the other in order that everything after the decimal point shall cancel.
100x - 10x = 90x = 154.\dot{4} - 15.\dot{4} = 154 - 15 = 139
Thus if we rearrange to make x the subject then,
x = \dfrac{139}{90}
Recurring Decimals to Fractions Worksheet and Example Questions
(NEW) Recurring Decimals to Fractions Exam Style Questions - MME
Level 6-7GCSENewOfficial MMERecurring Decimals to Fractions Drill Questions
Fractions to recurring decimals - Drill Questions
Level 6-7GCSE
Recurring Decimals to Fractions 2 - Drill Questions
Level 6-7GCSE
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now